Что такое вершина треугольника 3 класс

Вершина треугольника – определение

В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Определение вершины треугольника

В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.

Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Рис. 2. Обозначение вершин в треугольнике.

Характеристики понятия

Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).

Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.

Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.

Использование вершины треугольника

При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Рис. 3. Свойство внешнего угла треугольника.

Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?

Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.

Источник

Вершина треугольника

Всего получено оценок: 190.

Всего получено оценок: 190.

В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Определение вершины треугольника

В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.

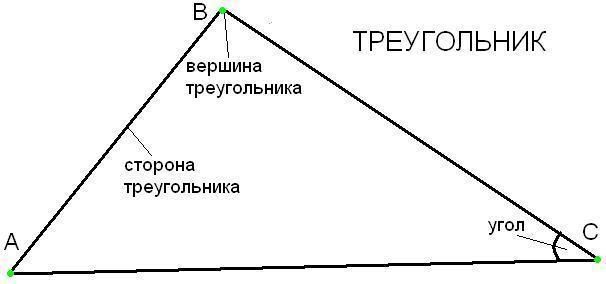
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Характеристики понятия

Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).

Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.

Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.

Использование вершины треугольника

При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?

Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.

Источник

Треугольник

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса ABC.

Каждый треугольник имеет три биссектрисы.

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана ABC.

Источник

Геометрическая фигура: треугольник

В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.

Определение треугольника

Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.

Углы можно, также, обозначать с помощью специального знака “∠“:

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.

2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Свойства треугольника

1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:

Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.

2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.

3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.

Примеры задач

Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.

Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.

Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4

Источник

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник