Что такое вершина ломаной в математике
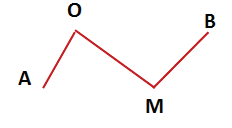
Ломаная линия
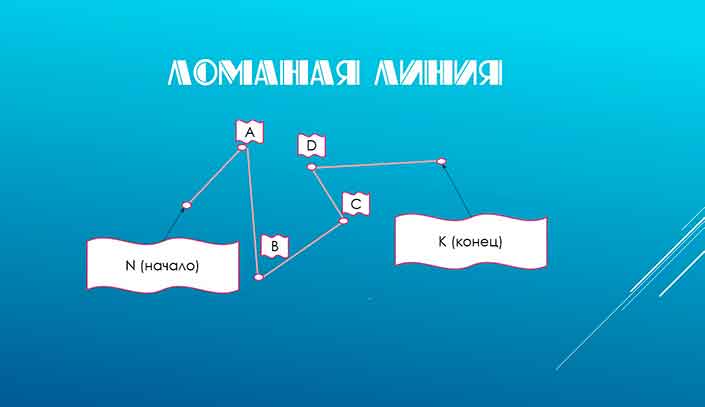
Ломаная линия бывает незамкнутая.
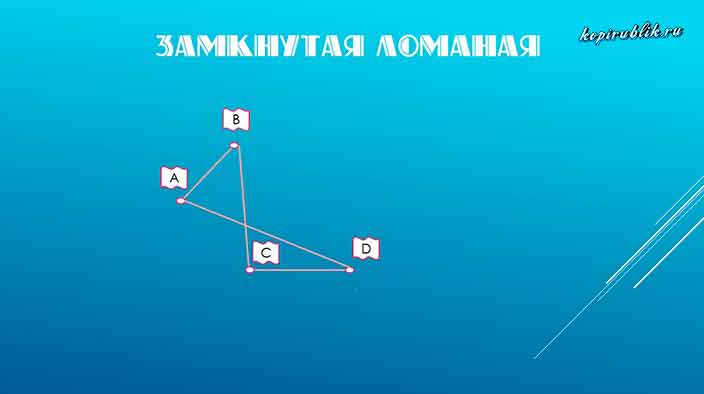
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
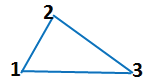
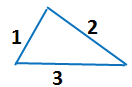
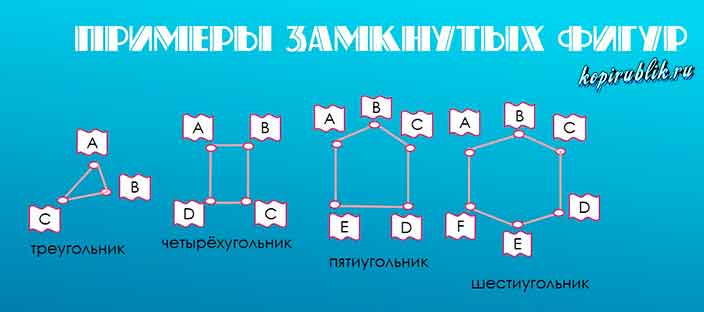
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
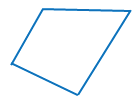
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
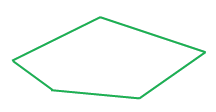
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
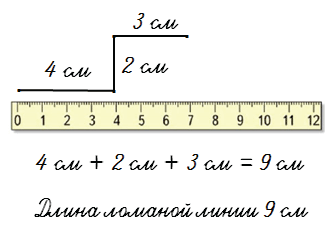
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Определение и характеристики ломаной геометрической фигуры
Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.
Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.
Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.
Звенья, вершины и длина
Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:
В целом такую совокупность принято называть ABCDE или EDCBA.
Обратите внимание: что такое луч в геометрии.
Разновидности
В геометрии принято различать несколько разновидностей по структуре:
Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.
Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.
Многоугольники
Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.
Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.
Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.
Свойства
Ниже приведены основные свойства, общие для всех многоугольников:
Треугольники
Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.
Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.
Различают следующие виды треугольников:
Четырехугольники
Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.
Если все углы у четырехугольника прямые — это прямоугольник.
Правильный четырехугольник носит название квадрата.
Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.
Ломаная линия — что это такое простыми словами
Ломаная линия — определение
Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.
Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.
Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.
Таким образом, фигура в обязательном порядке отвечает нескольким признакам:
Обозначение ломаной линии
Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.
Из чего состоит ломаная линия
Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.
Признак замкнутости ломаной линии
Классификация ломаных линий прежде всего осуществляется по свойству замыкания.
Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:
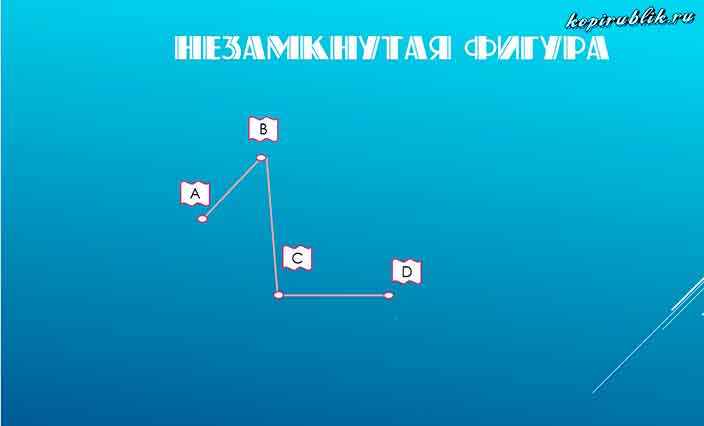
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.
Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».
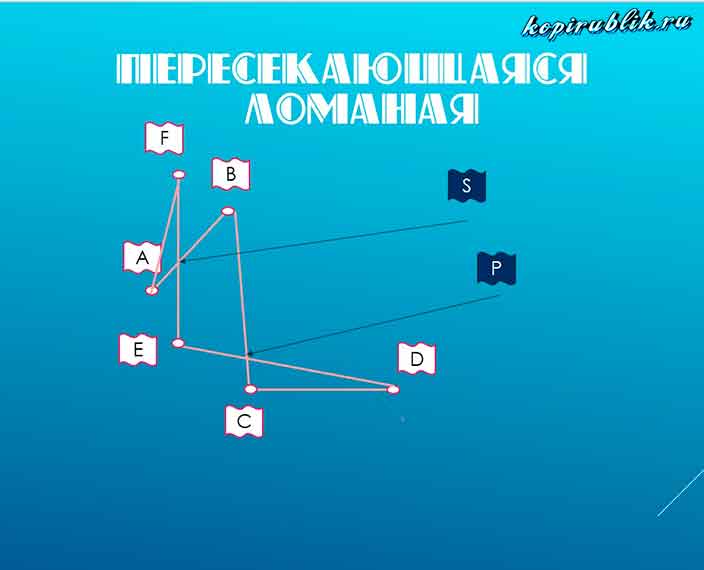
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.
На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.
Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:
Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.
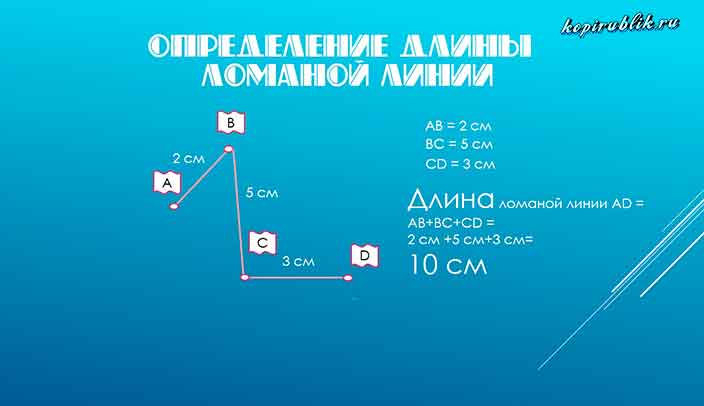
Как измерить длину ломаной линии
Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.
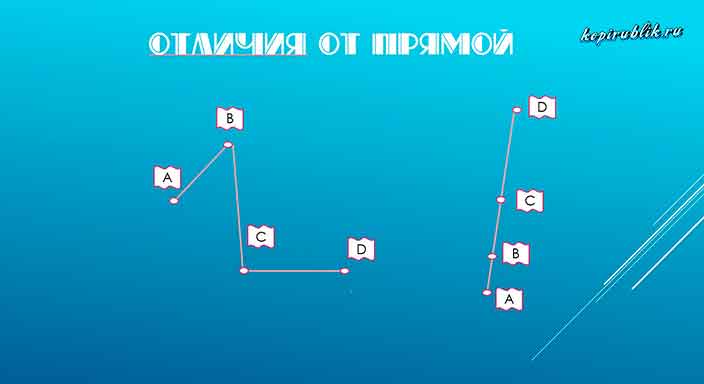
Чем ломаная линия отличается от прямой
При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.
Примеры ломаных линий в быту
В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.
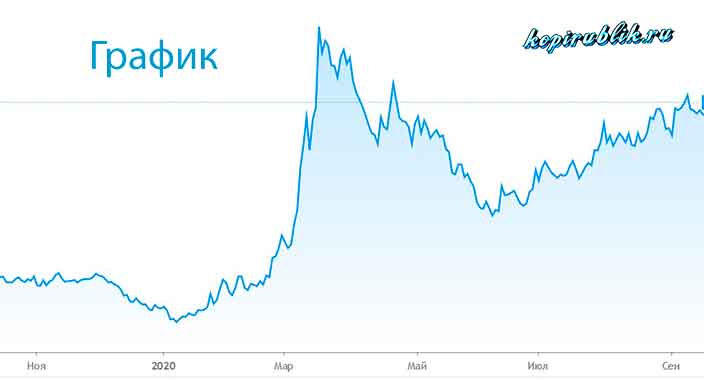
Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.
Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.
Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.
Ломаная
Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_
Можно дать и другое определение ломаной:
 |
Невырожденная ломаная
Ломаная, описанная в определении 1 называется невырожденной ломаной.
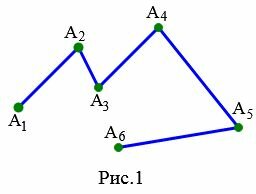
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.
Вырожденная ломаная
 |
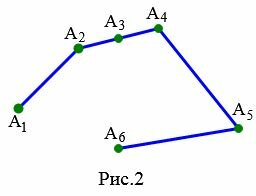На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.
Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.
Звенья ломаной
Звеньями называют отрезки, из которых состоит ломаная.
Вершины ломаной
Конечные точки звеньев ломаной называются вершинами.
На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).
Смежные звенья ломаной
Смежные звенья ломаной − это звенья имеющие общую вершину.
На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).
Смежные вершины ломаной
Смежными вершинами ломаной называют вершины одного звена ломаной.
На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).
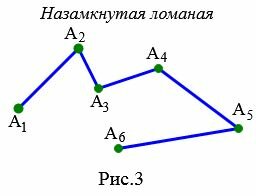
Незамкнутая ломанная
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).
 |
Замкнутая ломанная
 |
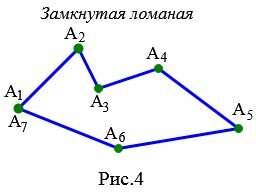На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.
Ломаная с самопересечением
Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.
 |
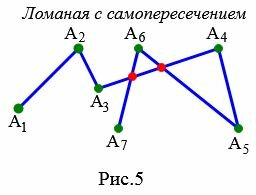Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).
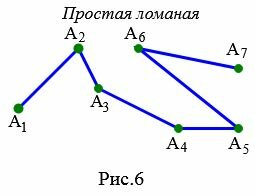
Простая ломаная
Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.
 |
Длина ломаной
Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_
Теорема. Длина ломаной больше расстояния между первым и последним точками.
 |
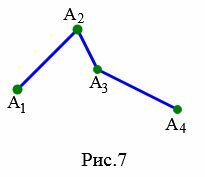Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:
Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:
В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.
В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:
Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками. 
Аналогично доказывается теорема для ломанной с любым количеством звеньев.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии