Что такое вершина графа в информатике
Графы: основы теории, алгоритмы поиска
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Графы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
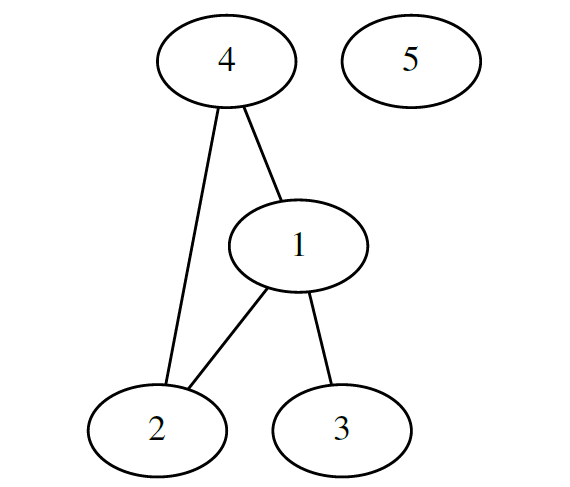
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Вторым признаком является отсутствие или наличие кратных ребер.

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.3. Графические информационные модели
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта. Примеры схем приведены на рис. 1.5.
Рис. 1.5. Примеры схем, используемых на уроках физики, биологии, истории
Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.
Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.
График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
1.3.2. Графы
Если некоторые объекты изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой; при этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной.
Граф называется неориентированным, если его вершины соединены рёбрами (рис. 1.6, а). Вершины ориентированного графа соединены дугами (рис. 1.6, б). Путь — это последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую.
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. На рис. 1.6, в с помощью взвешенного неориентированного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Рис. 1.6. Графы
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс1* высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Ресурс «Живая Родословная» (145555) — инструмент для формирования и анализа генеалогических деревьев, содержащий примеры родословных. С его помощью вы можете изучить генеалогические деревья многих известных семей и построить генеалогическое дерево своей семьи (http://sc.edu.ru/).
Класс — множество объектов, обладающих общими признаками.
1.3.3. Использование графов при решении задач
Графы удобно использовать при решении некоторых классов задач.
Пример 1. На рисунке 1.7 изображена схема дорог, связывающих торговые точки А, В, С, D, Е. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки Е?
Рис. 1.7. Схема дорог, представленная ориентированным графом
В вершину Е можно попасть только из вершин С и D. Если мы будем знать число путей из вершины А в вершину С и из вершины А в вершину D, то, сложив их, получим искомое число путей из А в Е. Действительно, для того чтобы попасть из вершины А в вершину Е, мы просто все пути из вершины А в вершину С дополним дугой СЕ, а пути из вершины А в вершину D дополним дугой DE. Число путей при этом не изменится. Итак, число путей из вершины А в вершину Е равно сумме путей из А в С и из А в П.
Можно сказать, что наша задача распалась на две более простые задачи. Решим каждую из них в отдельности.
В вершину С можно попасть непосредственно из вершины А и из вершины В. В свою очередь, существует единственный путь из вершины А в вершину В. Таким образом, из вершины А в вершину С можно попасть двумя путями: 1 (напрямую из А) + 1 (через В) = 2.
Попробуйте доказать, что путь из вершины А в вершину В — единственный.
Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин А, В и С:
1 (напрямую из А) + 1 (через В) + 2 (через С) = 4.
Итак, существуют четыре пути из вершины А в вершину D.
Теперь выполним подсчёт путей из А в Е:
2 (через С) + 4 (через D) = 6.
Решение задачи будет гораздо проще, если двигаться от вершины А (начало маршрута) к вершине Е и проставлять веса вершин — число путей из А в текущую вершину (рис. 1.8). При этом вес вершины А можно принять за 1. Действительно, существует единственный способ попасть из А в А — оставаться на месте.
Рис. 1.8. Схема дорог, представленная взвешенным ориентированным графом
Пример 2. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.9.
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
Рис. 1.9. Дерево для решения задачи о записи трёхзначных чисел
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. (Вспомните правило умножения из комбинаторики!)
Пример 3. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.10).
Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:
1) крестьянин перевозит лису;
2) крестьянин возвращается;
3) крестьянин перевозит собаку;
4) крестьянин возвращается с лисой;
5) крестьянин перевозит гуся;
6) крестьянин возвращается;
7) крестьянин перевозит лису.
Пример 4. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 1.11 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Рис. 1.11. Дерево игры
САМОЕ ГЛАВНОЕ
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы.
Граф состоит из вершин, связанных линиями — рёбрами или дугами. Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весами вершин (рёбер, дуг).
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Алгоритмы на графах — Часть 0: Базовые понятия
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.

На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| 2 ).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).

На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»







