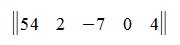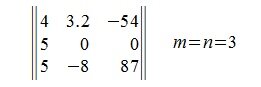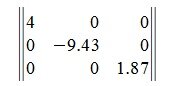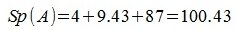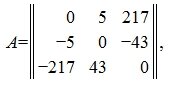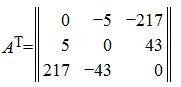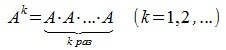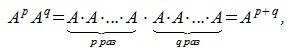Что такое верхняя треугольная матрица
Треугольная матрица
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.
Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:
Любую ненулевую матрицу 
путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.
Любая квадратная матрица, имеющая отличные от нуля главные миноры, представима произведением двух матриц: верхнетреугольной, и нижнетреугольной. Разложение единственно, если фиксированы (заранее оговорены) элементы главной диагонали одной из них.
Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.
Свойства
См. также
Полезное
Смотреть что такое «Треугольная матрица» в других словарях:
треугольная матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] треугольная матрица Квадратная матрица, у которой равны нулю все элементы, расположенные под или над главной диагональю (ср. Диагональная матрица). В первом случае имеем… … Справочник технического переводчика
Треугольная матрица — [triangular matrix] квадратная матрица, у которой равны нулю все элементы, расположенные под или над главной диагональю (ср. Диагональная матрица). В первом случае имеем верхнюю Т.м. во втором нижнюю … Экономико-математический словарь
ТРЕУГОЛЬНАЯ МАТРИЦА — квадратная матрица, у к рой все элементы, расположенные ниже (или выше) главной диагонали, равны нулю. В первом случае матрица наз. верхней треугольной матрицей, во втором нижней треугольной матрицей. Определитель Т. м. равен произведению всех ее … Математическая энциклопедия
Треугольная матрица МОБ — [triangular input output matrix] матрица коэффициентов межотраслевого баланса (МОБ), соответствующая такой производственной системе, в которой любой продукт может затрачиваться в своем собственном производстве и в производстве любого следующего… … Экономико-математический словарь
треугольная матрица МОБ — Матрица коэффициентов межотраслевого баланса (МОБ), соответствующая такой производственной системе, в которой любой продукт может затрачиваться в своем собственном производстве и в производстве любого следующего за ним продукта, но никакой… … Справочник технического переводчика
Верхняя треугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Блочно-треугольная матрица — [partitionned triangular matrix] – матрица, которую можно разбить на подматрицы таким образом, чтобы по одну сторону ее «главной диагонали«, составленной из подматриц, стояли нули. Примерами блочно треугольных матриц могут служить… … Экономико-математический словарь
блочно-треугольная матрица — Матрица, которую можно разбить на подматрицы таким образом, чтобы по одну сторону ее «главной диагонали«, составленной из подматриц, стояли нули. Примерами блочно треугольных матриц могут служить треугольная матрица и блочно диагональная матрица … Справочник технического переводчика
Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь
Верхняя треугольная матрица
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.
Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:
Любую ненулевую матрицу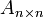 
путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.
Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.
Свойства
См. также
Полезное
Смотреть что такое «Верхняя треугольная матрица» в других словарях:
Треугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица … Википедия
Верхнетреугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Косотреугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Нижнетреугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
LU-разложение — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Проставив сноски, внести более точные указания на источники. Добавить иллюстрации … Википедия
SFLASH — SFLASH асимметричный алгоритм цифровой подписи рекомендованный проектом NESSIE European в 2003 году. SFLASH основан на Matsumoto Imai(MI) схеме, так же называемой C*. Алгоритм принадлежит к семейству многомерных схем с открытым ключом, то… … Википедия
ОРТОГОНАЛИЗАЦИЯ — процесс ортогонализации, алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V. Наиболее известным является… … Математическая энциклопедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
РЕЛАКСАЦИИ МЕТОД — ослабления м е т о д, метод итерационного решения системы линейных алгебраич. уравнений Ах=b, элементарный шаг к рого состоит в изменении только одной компоненты вектора неизвестных, причем номера изменяемых компонент выбираются в нек ром циклич … Математическая энциклопедия
Верхнетреугольная матрица
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.
Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:
Любую ненулевую матрицу 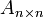путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.
Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.
Свойства
См. также
Полезное
Смотреть что такое «Верхнетреугольная матрица» в других словарях:
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Треугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица … Википедия
Верхняя треугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Косотреугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Нижнетреугольная матрица — Треугольная матрица квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Пример верхнетреугольной матрицы Верхнетреугольная матрица квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.… … Википедия
Квадратная матрица — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Разложение матрицы — Разложение матрицы представление матрицы в виде произведения матриц, обладающих некоторыми определёнными свойствами, например, ортогональностью, симметричностью, диагональностью и потому облегчающих рассмотрение свойств линейного… … Википедия
Список матриц — Структура матрицы Здесь собраны наиболее важные классы матриц, используемые в математике, науке (в целом) и прикладной науке (в частности). Под матрицей понимается прямоугольный массив чисел … Википедия
QR-разложение — У этого термина существуют и другие значения, см. QR. разложение матрицы представление матрицы в виде произведения унитарной (или ортогональной матрицы) и верхнетреугольной матрицы. Определение Матрица размера с комплексными элементами… … Википедия
СОДЕРЖАНИЕ
Описание
Примеры
верхнетреугольная, и эта матрица
Прямая и обратная подстановка
Обратите внимание, что это не требует инвертирования матрицы.
Прямая замена
Матричное уравнение L x = b можно записать в виде системы линейных уравнений
В результате получаются следующие формулы:
Матричное уравнение с верхнетреугольной матрицей U может быть решено аналогичным образом, только в обратном направлении.
Приложения
Характеристики
Детерминант и перманентный треугольной матрицы равен произведению диагональных элементов, так как могут быть проверены прямым вычислением.
Особые формы
Унитреугольная матрица
Строго треугольная матрица
Атомная треугольная матрица
Возможность треугольной формы
Любая комплексная квадратная матрица треугольная. Фактически, матрица A над полем, содержащим все собственные значения A (например, любая матрица над алгебраически замкнутым полем ), подобна треугольной матрице. Это можно доказать с помощью индукции по тому факту, что A имеет собственный вектор, взяв фактор-пространство по собственному вектору и проведя индукцию, чтобы показать, что A стабилизирует флаг и, таким образом, является треугольным по отношению к базису этого флага.
Одновременная треугольная возможность
Алгебры треугольных матриц
Верхнюю треугольность сохраняют многие операции:
Все эти результаты остаются в силе, если верхний треугольник полностью заменен нижним треугольником ; в частности, нижнетреугольные матрицы также образуют алгебру Ли. Однако операции смешивания верхних и нижних треугольных матриц, как правило, не дают треугольных матриц. Например, сумма верхней и нижней треугольных матриц может быть любой матрицей; произведение нижнего треугольника на верхнюю треугольную матрицу также не обязательно треугольное.
Борелевские подгруппы и борелевские подалгебры
Примеры
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
(i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
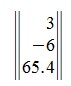
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
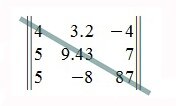
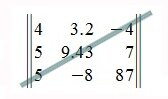
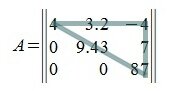
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство: