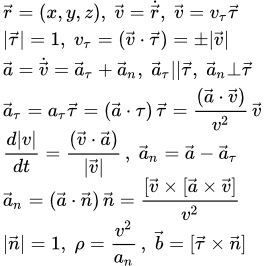Что такое векторный способ
Что такое векторный способ
Движение. Виды движений. Описание движения. Система отсчета.
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
А) Равномерное прямолинейное движение материальной точки.
Б) Равноускоренное прямолинейное движение материальной точки.
В) Движение тела по дуге окружности с постоянной по модулю скоростью.
Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.
1. Векторный способ описания движения
ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.
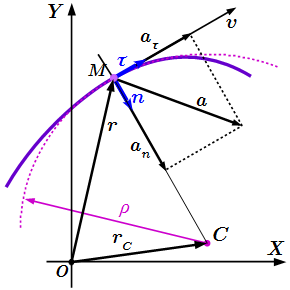
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.
При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.
В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.
2. Координатный способ описания движения
ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.
В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.
Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )
Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: rx = x , ry = y , rz = z .
3. Естественный способ описания движения
ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.
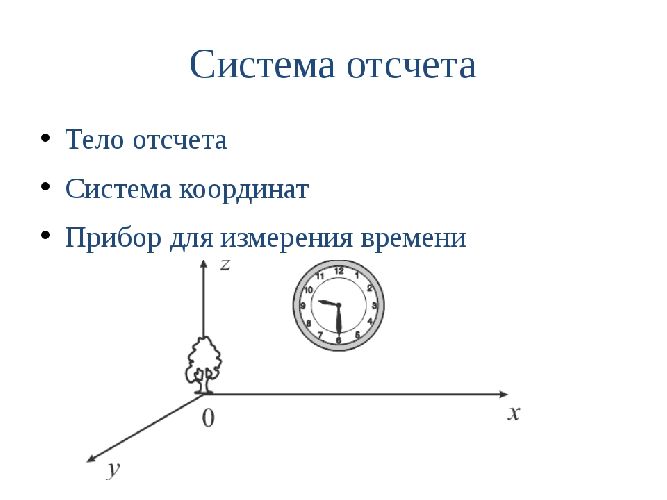
Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.
Способы описания движения. Векторный способ. Координатный способ
По этой ссылке вы найдёте полный курс лекций по математике:
кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси. Рис. 1 Рис. 2 1.
Векторный способ. В этом способе положение материальной точки А задаётся с помощью так называемого радиус-вектора г, который представляет совой вектор, проведённый из точки О, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку А (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени г = r(t).
Геометрическое место концов радиус-вектора г (t) называют траекторией точки А. В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка А после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени At тело (точка А) переместилось из начального положения 1 с радиус-вектором Т\ в конечное положение 2 с радиус-вектором Т\ (рис. 2). Приращение А г радиус-вектора тела в таком случае равно: Вектор Аг, соединяющий начальное и конечное положения тела, называют перемещением тела. Отношение Аг/At называют средней скоростью (средним вектором скорости) vcp тела за время At: Способы описания движения.
Векторный способ. Координатный способ. Естественный (или траекторный) способ Вектор vcp колли неарен и сонаправлен с вектором Аг, так как отличается от последнего лишь скалярным неотрицательным множителем 1 / Аг. Предложенное определение средней скорости справедливо для любых значений At, кроме Д/ = 0. Однако ничто не мешает брать промежуток времени At сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени t или в конкретной точке траектории. С этой целью промежуток времени At устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение Аг. При этом отношение А/ / At стремится к определённому значению, не зависящему от At. Величина, к которой стремится отношение Аг / At при стремлении At к нулю, называется мгновенной скоростью v: Теперь заметим, что чем меньше At, тем ближе направление Аг к направлению касательной к траектории в данной точке.
Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела. В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости v тела (материальной точки). Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения.
Его определяют через отношение приращения вектора скорости Av тела к промежутку времени А/, в течение которого это приращение произошло.
Возможно вам будут полезны данные страницы:
Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (м/с) и метр на секунду в квадрате (м/с2 2. Координатный способ. В этом способе положение материальной точки А на плоскости в произвольный момент времени t определяется двумя координатами хну, которые представляют собой проекции радиус-вектора г тела на оси Ох и Оу соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями V= y(t).
| Если эти функции известны |
то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости v можно спроецировать на оси координат и определить таким образом скорости i\ и v.. изменения координат тела (рис. 4). В самом деле, vx и vy будут равны значениям, к которым стремятся соответственно отношения Ах/А t и Ay/At при стремлении к нулю промежутка времени At. Аналогично с помощью проецирования вектора а определяются ускорения ах и ах тела по направлениям координатных осей.
Само слово «средняя» означает усреднение по времени. Пример 1. Городской троллейбус утром вышел на маршрут, а через 8 часов, проехав в общей сложности 72 км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость vcp и средняя путевая скорость г>ср троллейбуса? Способы описания движения.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Векторный способ описания движения материальной точки – формулы с примерами, краткое определение
Кинематика описывает движение, не рассматривая его причины. Для такого описания может использоваться несколько способов. Кратко рассмотрим векторный способ описания движения материальной точки.
Описание движения
Описание движения — это ответ на вопрос, как менялось положение точки в пространстве со временем. Чтобы получить этот ответ, необходимо выбрать способ сопоставления моментов времени и положения в пространстве, способ измерения времени и способ определения положения точки.
Способом сопоставления может стать таблица или математическая функция. Таблица проще, однако она описывает только определенные моменты времени. Математическая функция описывает любой момент времени, поэтому используется чаще.
Для определения времени и положения в пространстве используется система отсчета.
Рис. 1. Система отсчета в физике.
Моменты времени отмечаются с использованием некоторого эталонного процесса. В прошлом таким процессом было суточное вращение Земли, в настоящее время используется частота излучения возбужденных атомов цезия.
Положение в пространстве может задаваться несколькими способами, одним из которых является векторный.
Радиус-вектор
Как известно из геометрии, вектор — это отрезок на плоскости или в пространстве, для которого можно указать начало и конец. При этом для вектора важны не абсолютные координаты начала и конца в пространстве, а их разница. Положение вектора можно менять, сохраняя ее (параллельный перенос), сам вектор при этом не изменится.
Рис. 2. Радиус-вектор точки.
Векторная функция движения
При описании движения векторным способом задается соответствие между моментами времени и радиус-вектором:
$$overrightarrow r=overrightarrow r(t)$$
Такая запись, как правило, заметно компактнее и проще, чем работа непосредственно с координатами точки. Однако математические действия с векторами требуют проецирования вектора на оси координат, алгебраического сложения длин, взятых с нужным знаком, и затем восстановления результата по проекциям. Поэтому векторный способ описания больше подходит тогда, когда требуется вывод законов и формул. В этом случае векторное уравнение позволяет выделить суть закона или формулы, не загромождая формулировки математическими выкладками.
Поэтому для физических законов векторная форма находит самое широкое применение. Она имеет компактную однострочную форму, при этом описывая движение сразу по всем координатным осям.
Рис. 3. Векторный способ задания движения точки.
Что мы узнали?
В физике широкое применение находит векторный способ описания движения точки. Он имеет такую же точность, как координатный способ, но при этом учитывает сразу все координатные оси и записывается гораздо более компактно. Поэтому такой способ описания движения очень подходит для законов и формул: он позволяет выделить суть закона, не загромождая формулировку.
Векторный способ задания движения точки
Введение
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость и ускорение точки M при векторном способе задания движения
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Нормальное ускорение
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Векторный способ описания движения материальной точки
Всего получено оценок: 68.
Всего получено оценок: 68.
Кинематика описывает движение, не рассматривая его причины. Для такого описания может использоваться несколько способов. Кратко рассмотрим векторный способ описания движения материальной точки.
Описание движения
Описание движения — это ответ на вопрос, как менялось положение точки в пространстве со временем. Чтобы получить этот ответ, необходимо выбрать способ сопоставления моментов времени и положения в пространстве, способ измерения времени и способ определения положения точки.
Способом сопоставления может стать таблица или математическая функция. Таблица проще, однако она описывает только определенные моменты времени. Математическая функция описывает любой момент времени, поэтому используется чаще.
Для определения времени и положения в пространстве используется система отсчета.
Рис. 1. Система отсчета в физике.
Моменты времени отмечаются с использованием некоторого эталонного процесса. В прошлом таким процессом было суточное вращение Земли, в настоящее время используется частота излучения возбужденных атомов цезия.
Положение в пространстве может задаваться несколькими способами, одним из которых является векторный.
Радиус-вектор
Как известно из геометрии, вектор — это отрезок на плоскости или в пространстве, для которого можно указать начало и конец. При этом для вектора важны не абсолютные координаты начала и конца в пространстве, а их разница. Положение вектора можно менять, сохраняя ее (параллельный перенос), сам вектор при этом не изменится.
Векторная функция движения
При описании движения векторным способом задается соответствие между моментами времени и радиус-вектором:
$$\overrightarrow r=\overrightarrow r(t)$$
Такая запись, как правило, заметно компактнее и проще, чем работа непосредственно с координатами точки. Однако математические действия с векторами требуют проецирования вектора на оси координат, алгебраического сложения длин, взятых с нужным знаком, и затем восстановления результата по проекциям. Поэтому векторный способ описания больше подходит тогда, когда требуется вывод законов и формул. В этом случае векторное уравнение позволяет выделить суть закона или формулы, не загромождая формулировки математическими выкладками.
Поэтому для физических законов векторная форма находит самое широкое применение. Она имеет компактную однострочную форму, при этом описывая движение сразу по всем координатным осям.
Что мы узнали?
В физике широкое применение находит векторный способ описания движения точки. Он имеет такую же точность, как координатный способ, но при этом учитывает сразу все координатные оси и записывается гораздо более компактно. Поэтому такой способ описания движения очень подходит для законов и формул: он позволяет выделить суть закона, не загромождая формулировку.