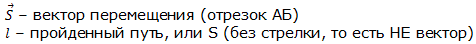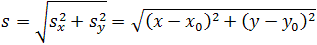Что такое векторное перемещение в физике

Траектория, путь, перемещение. Векторные величины в физике

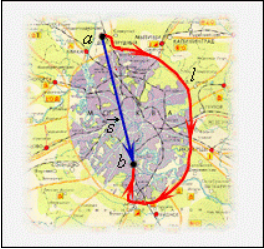
п.1. Траектория и путь

Траектория полета баскетбольного мяча

Траектория полета на Марс и обратно

Пример зависимости траектории от системы отсчета
Жук сел в центр больших башенных часов и пополз по минутной стрелке.
За час, двигаясь с постоянной скоростью, он дополз до конца стрелки.

В системе отсчета, связанной с минутной стрелкой, траектория жука – отрезок прямой.

В системе отсчета, связанной с циферблатом, траектория жука – спираль Архимеда.

Путь также зависит от выбора системы отсчета, как и траектория.
Допустим, что минутная стрелка, по которой ползал жук в нашем примере, имеет длину L=7,5 м. Тогда в системе отсчета, связанной со стрелкой, путь жука s₁=L=7,5 м.
Для спирали Архимеда длина описанной дуги также известна и равна s₁≈2,83L≈21,2 м. Т.е. в системе отсчета, связанной с циферблатом, путь жука почти в 3 раза больше.

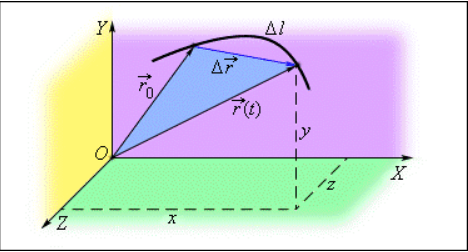
п.2. Перемещение

Пример перемещения в разных системах отсчета

п.3. Понятие вектора и суммы векторов

Примеры векторов на плоскости и их обозначений:

Вектор \(\overrightarrow\) является обратным для вектора \(\overrightarrow\), т.е. \(\overrightarrow=-\overrightarrow\).
При этом оба вектора равны по модулю: \(|\overrightarrow|=|\overrightarrow|\).
Сумма двух взаимно обратных векторов равна нулю: \(\overrightarrow+\overrightarrow=\overrightarrow-\overrightarrow=0\).
С точки зрения физики это можно пояснить так: точка переместилась из A в B, а затем вернулась обратно в A. В итоге перемещение равно 0.

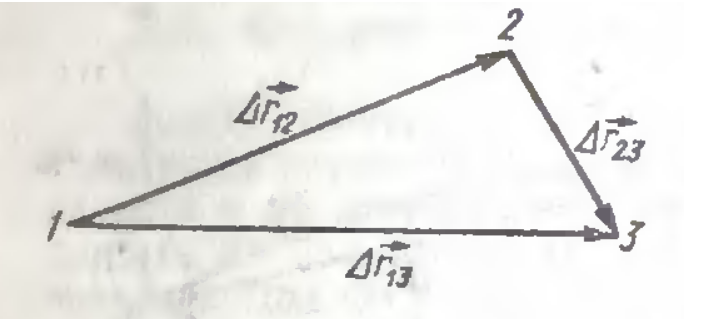
С точки зрения физики правило треугольника можно пояснить так: точка переместилась из A в B, а затем из B в C. В итоге произошло перемещение из A в C, т.е. \(\overrightarrow\).

п.4. Задачи

Задача 1. Пассажир движущегося по прямой круизного лайнера прогуливается по палубе, от правого борта к левому и обратно. Постройте траектории движения пассажира:
а) относительно лайнера;
б) относительно Земли.

а) относительно лайнера;

Траектория – отрезок между бортами, по которому пассажир движется туда и обратно.

б) относительно Земли.

Траектория – кривая (синусоида), которая получается как сумма движений пассажира от одного борта к другому и движения лайнера вперед.

Задача 2. Платформа длиной l движется по дороге, а человек движется по платформе.

Каков путь человека: а) относительно платформы; б) относительно дороги? в) Каков путь переднего колеса платформы относительно дороги?

а) Путь человека относительно платформы равен длине платформы l.
б) Путь человека относительно дороги равен s.
в) Путь переднего колеса платформы относительно дороги (s-l).

Задача 3. Мяч, брошенный вертикально вверх, поднялся на высоту 7 м и упал обратно.
Чему равен: а) его путь; б) перемещение?

а) Путь равен сумме пройденных расстояний вверх и вниз: s=7+7=14 (м)
б) Перемещение равно \(|\overrightarrow|=0\), т.к. мяч упал в исходную точку.

Задача 4. Вертолет пролетел 400 км на север, 200 км на восток и 400 км на юг.
Начертите схему движения и определите путь и перемещение вертолета.

Ответ: s=1100 км; \(|\overrightarrow|=300\ \)км, на восток

Задача 5. В сундуке старого пирата найдена старая карта, на которой точкой отмечен старый дуб. На обратной стороне карты есть надпись, которую удалось расшифровать: «30 шагов на север, 20 шагов на запад, 50 шагов на юг, 50 шагов на восток, 20 шагов на север. Копай!». Начертите схему движения, найдите путь и перемещение от дуба к кладу в шагах и метрах, если в одном шаге 70 см.

Строим прямоугольную систему координат, дуб – в начале отсчета.
Откладываем векторы перемещений и отмечаем координаты на осях:

Получаем, что клад находится в точке F, расположенной в 30 шагах на восток от дуба.
Путь из точки A в точку F равен сумме длин всех отложенных векторов:

s = 30+20+50+50+20=170 (шагов)
s = 170 · 0,7 = 119 (м)

Перемещение из точки A в точку F равно вектору \(\overrightarrow,\ \overrightarrow=\overrightarrow\).
Модуль перемещения равен длине отрезка AF: \begin |\overrightarrow|=AB=30\ \text<(шагов)>\\ |\overrightarrow|=30\cdot 0,7=21\ \text <(м)>\end
Ответ: s=119 м; \(|\overrightarrow|=21\ \)м, на восток

Источник

Траектория, длина пути, вектор перемещения

Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.

Виды движений тела

Существуют несколько видов движений и траекторий твердого тела:

Перемещение тела

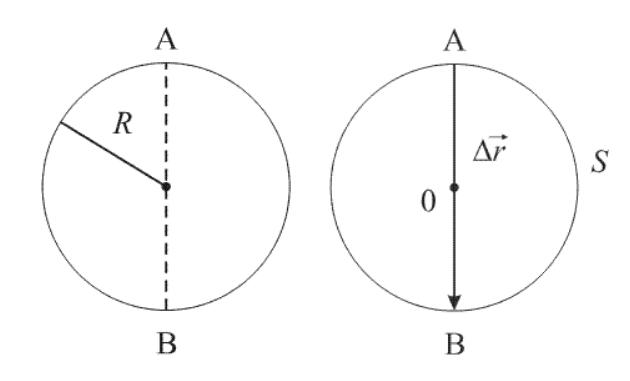
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.

Перемещение принято считать векторной величиной. Этот отрезок имеет направление.

Путь – скалярная величина. Считается числом.

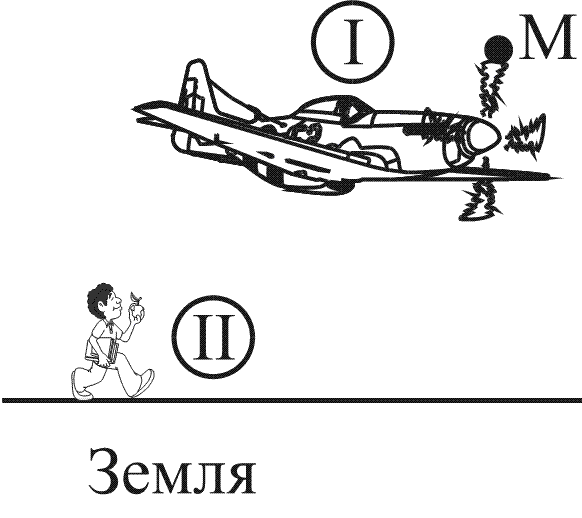
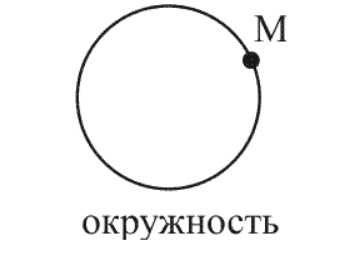
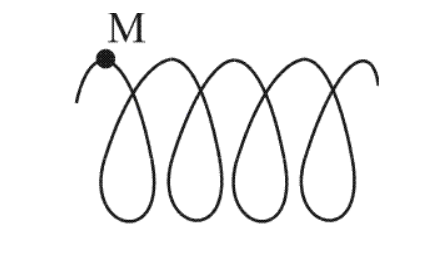
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.

Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:

Подставляем числовые значения и получаем:

Источник

Вектор перемещения

Перемещение в классической механике — направленный отрезок, характеризующий изменение положения материальной точки в пространстве. Обладает свойствами вектора, поэтому является векторной величиной. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).

Перемещением также называют процесс изменения положения.

Можно определить перемещение, как изменение радиус-вектора точки: .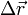

Модуль перемещения совпадает с пройденным путём в том и только в том случае, если при движении направление перемещения не изменяется. При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше.

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго:

.

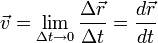
См. также

Ссылки

ПеремещениеКлассическая механикаНаправлениеПо вертикали (Вверх•Вниз)•По горизонтали (Влево•Вправо•Вперёд•Назад)СкоростьМгновенно•Очень быстро•Быстро•Средне•Медленно•Очень медленноНаука:Физика

Полезное

Смотреть что такое «Вектор перемещения» в других словарях:

вектор перемещения — transliacijos vektorius statusas T sritis fizika atitikmenys: angl. translation vector; translational vector vok. Schiebvektor, m; Translationsvektor, m rus. вектор перемещения, m; вектор трансляции, m pranc. vecteur de translation, m … Fizikos terminų žodynas

вектор трансляции — transliacijos vektorius statusas T sritis fizika atitikmenys: angl. translation vector; translational vector vok. Schiebvektor, m; Translationsvektor, m rus. вектор перемещения, m; вектор трансляции, m pranc. vecteur de translation, m … Fizikos terminų žodynas

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

Вектор-строка — Ковариантным вектором (синоним: ковектор) в дифференциальной геометрии и смежных с ней физических концепциях называется вектор кокасательного пространства, то есть 1 форма. Естественным базисом для разложения ковекторов служит дуальный базис.… … Википедия

Вектор-столбец — Контравариантным вектором обычно называют совокупность (столбец) координат вектора в обычном базисе (то есть его контравариантных координат) или 1 формы в том же базисе, не являющемся, правда, для нее естественным. Контравариантный вектор в… … Википедия

предсказание перемещения — Техника межкадрового кодирования, применяемая в кодеках для сжатия сигнала движущегося изображения. В последовательности кадров каждый пиксел текущего кадра перемещен по сравнению с предшествующим кадром. Но соседние пикселы перемещаются… … Справочник технического переводчика

4-вектор — (четыре вектор, четырёхвектор) вектор в четырёхмерном пространстве Минковского. Координаты 4 вектора при переносе или повороте системы отсчёта преобразуются как соответствующие им координаты в пространстве Минковского. В 4 векторе одна… … Википедия

Контравариантный вектор — Контравариантным вектором обычно называют совокупность (столбец) координат вектора в обычном базисе (то есть его контравариантных координат) или 1 формы в том же базисе, не являющемся, правда, для неё естественным. Контравариантный вектор в… … Википедия

Аксиальный вектор — После инверсии, два вектора меняют свой знак, однако их векторное произведение остаётся неизменным. Аксиальный вектор … Википедия

Источник

Траектория

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

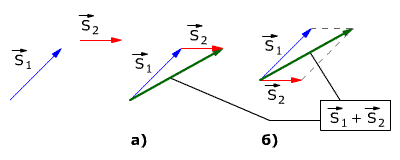
Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

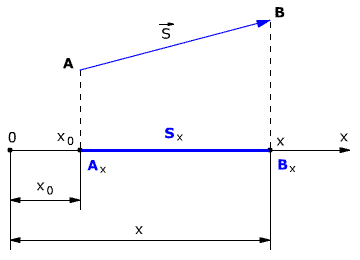
Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 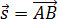(см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

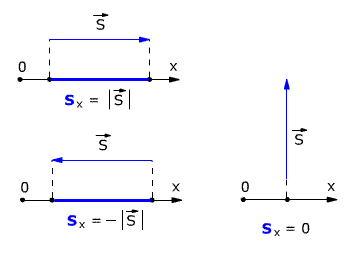
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

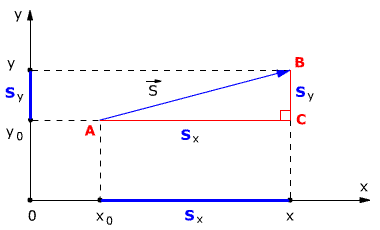
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

По теореме Пифагора

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

Траектория

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 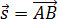(рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

По теореме Пифагора

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник