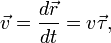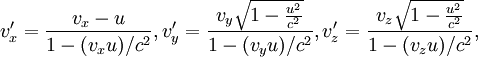Что такое векторная скорость
Скорость
Ско́рость (часто обозначается 
, от англ. velocity или фр. vitesse ) — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.
Содержание
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 
этой точки:
Здесь 
— модуль скорости, 
— направленный вдоль скорости единичный вектор касательной к траектории в точке .
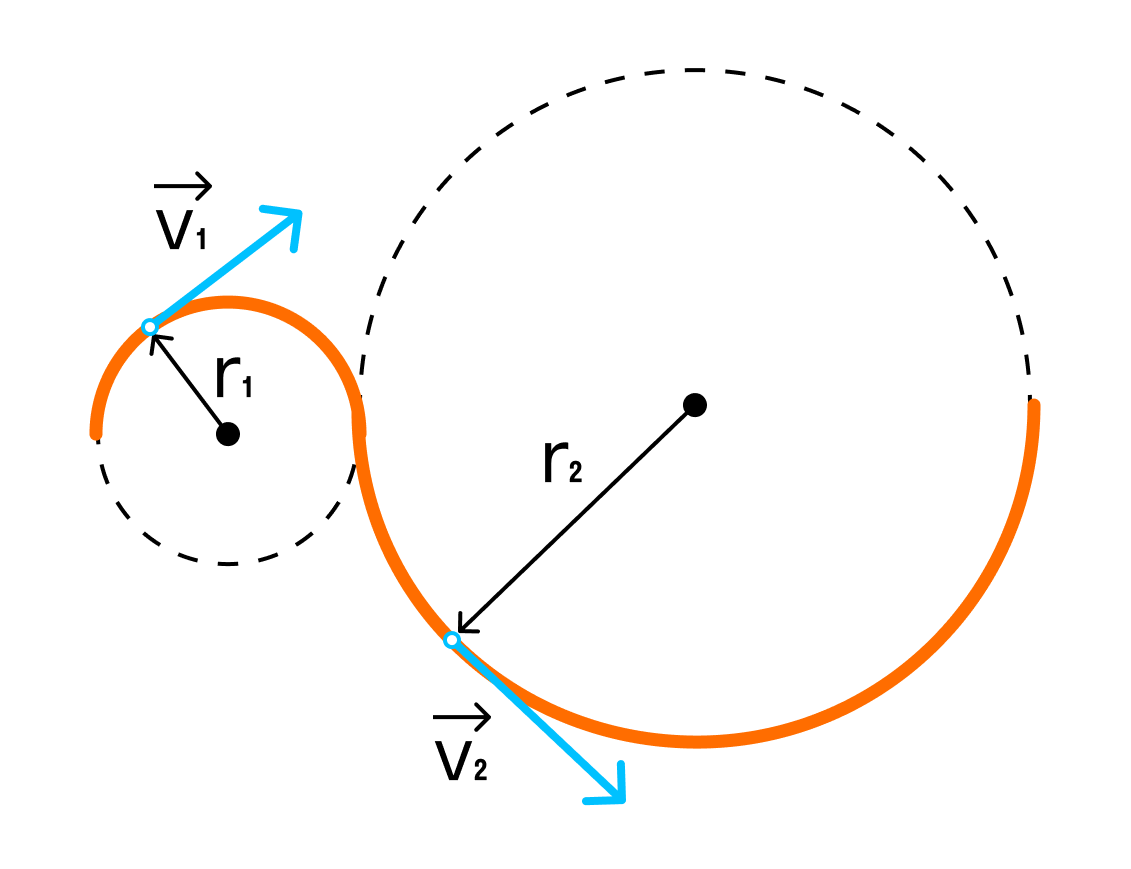
Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю) и тогда:
Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден.
Следует различать координатную и физическую скорости. При введении криволинейных или обобщённых координат положение тел описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями.
Мгновенная и средняя скорость
Следует отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Когда говорят о средней скорости, для различения, скорость согласно выше приведённому определению называют мгновенной скоростью.
Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.
В полярных координатах
Проекции скорости в декартовой системе координат
В то же время 
, поэтому
Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки:
.
Преобразование скорости
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна 
, то скорость тела при переходе в систему отсчёта S’ будет равна 
.
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Единицы измерения скорости
Соотношения между единицами скорости
См. также
Скорости волн  |
|---|
| Групповая скорость | Фазовая скорость | Фронтовая скорость | Сигнальная скорость |
Полезное
Смотреть что такое «Скорость» в других словарях:
СКОРОСТЬ — СКОРОСТЬ, скорости, мн. и, скоростей, жен. 1. только ед. (мн. спец.). Та или иная степень быстроты движения. Поезд двигался с большой скоростью. Автомобиль развил бешеную скорость. Эксплоатационная скорость поезда. Поставить рекорд скорости.… … Толковый словарь Ушакова
СКОРОСТЬ — в механике, одна из осн. кинематич. характеристик движения точки; величина векторная, определяемая равенством: v=dr/dt, где r радиус вектор точки, t время. При равномерном движении С. точки численно равна отношению пройденного пути s к промежутку … Физическая энциклопедия
СКОРОСТЬ — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Современная энциклопедия
Скорость — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Иллюстрированный энциклопедический словарь
СКОРОСТЬ — СКОРОСТЬ, и, мн. и, ей, жен. 1. Степень быстроты движения, распространения, действия. Развить с. Рекорд скорости бега. Двигаться на больших скоростях. С. звука (скорость распространения звуковых волн в среде). С. света (скорость распространения… … Толковый словарь Ожегова
скорость — скорость; мгновенная скорость Скорость точки жидкости, рассматриваемая как векторная функция переменных Эйлера … Политехнический терминологический толковый словарь
СКОРОСТЬ — СКОРОСТЬ, характеристика движения точки (тела), численно равная при равномерном движении отношению пройденного пути к промежутку времени, за которое этот путь пройден. Скорость (физическая) характеризует движение тела в определенном направлении,… … Научно-технический энциклопедический словарь
Скорость — Скорость, лазание на скорость вид скалолазания со следующими специфическими особенностями: большая протяженность большая высота, необходима страховка с веревкой на соревнованиях применяется верхняя страховка относительно несложные движения… … Энциклопедия туриста
Вектор скорости
Ско́рость (часто обозначается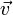 
, от англ. velocity или фр. vitesse ) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).
Содержание
Скорость тела в механике
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора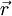 
этой точки:
Здесь v — модуль скорости,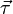 
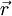
— направленный вдоль скорости единичный вектор касательной к траектории в точке .
Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.
Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.
Мгновенная и средняя скорость
Преобразование скорости
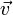
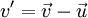
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна 
, то скорость тела в при переходе в систему отсчёта S’ будет равна 
.
Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Единицы измерения скорости
Соотношение между единицами скорости
См. также
Полезное
Смотреть что такое «Вектор скорости» в других словарях:
вектор скорости — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN velocity vector … Справочник технического переводчика
вектор скорости — greičio vektorius statusas T sritis fizika atitikmenys: angl. velocity vector vok. Geschwindigkeitsvektor, m rus. вектор скорости, m pranc. vecteur de vitesse, m; vecteur vitesse, m … Fizikos terminų žodynas
вектор скорости — greičio vektorius statusas T sritis Kūno kultūra ir sportas apibrėžtis Dydis, rodantis greičio statinę vertę (reikšmę) ir taško judėjimo kryptį. atitikmenys: angl. vector of velocity vok. Vektor der Geschwindigkeit, m rus. вектор скорости … Sporto terminų žodynas
вектор скорости ветра — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN wind vectorU … Справочник технического переводчика
вектор скорости вибрации — 3.4 вектор скорости вибрации : Вектор, содержащий шесть составляющих скорости вибрации (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации
вектор скорости вибрации n-го виброизолятора — 3.13 вектор скорости вибрации n го виброизолятора : Вектор скорости вибрации n го виброизолятора (матрица столбец), содержащий шесть составляющих (три линейные и три поворотные), направленных вдоль координатных осей x, y и z. Источник … Словарь-справочник терминов нормативно-технической документации
вектор скорости вибрации в n-й точке — 3.6 вектор скорости вибрации в n й точке : Вектор в n й точке (матрица столбец), содержащий три линейные составляющие скорости вибрации, направленные вдоль координатных осей х, у и z соответственно. Источник … Словарь-справочник терминов нормативно-технической документации
вектор — 01.03.02 вектор [ vector] (1)1): Величина, представляемая значением, направлением, смысловым содержанием и началом. 1)Терминологические статьи 01.03.02 и 01.03.03 относятся к одному понятию. Источник … Словарь-справочник терминов нормативно-технической документации
ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера
Основы механики для чайников. Часть 1: Кинематика
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
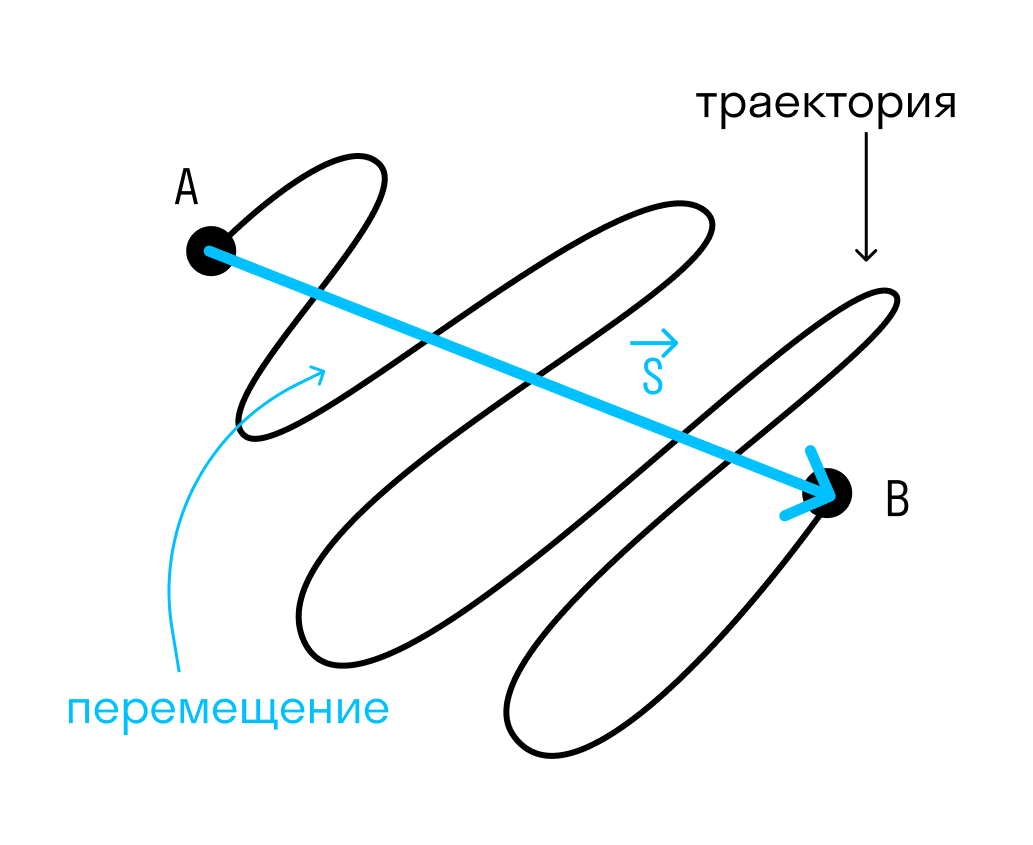
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
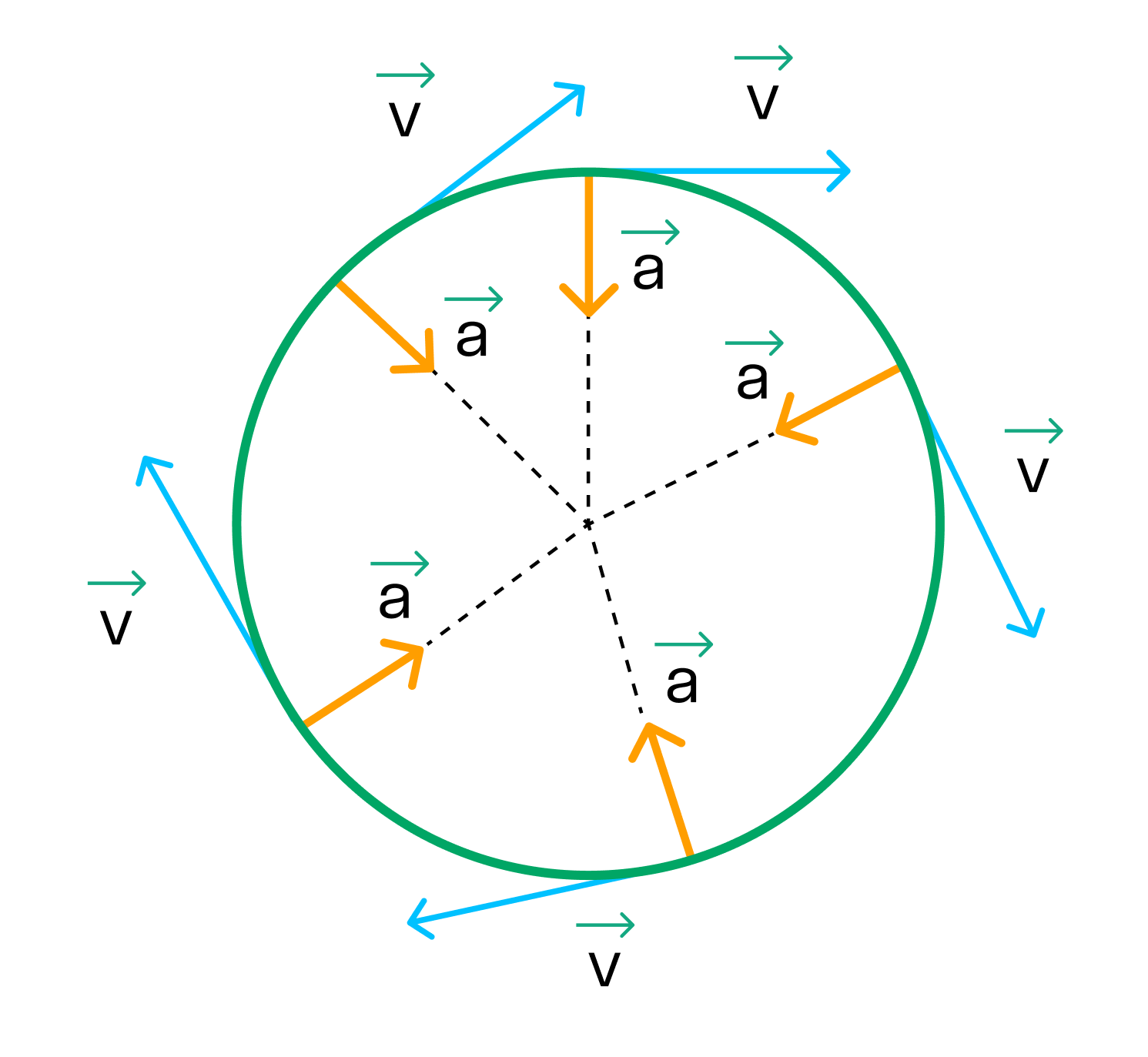
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Кинематика
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
Векторные величины (определяются значением и направлением)
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
→ →
V = S/t
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x0 + vxt
x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
