Что такое вектор нормали плоскости
Нормальный вектор плоскости
Вы будете перенаправлены на Автор24
Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.
Рисунок 1. Векторы в трехмерной системе координат. Автор24 — интернет-биржа студенческих работ
Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.
$Ax + D = 0 \\ By + D = 0 \\ Cz + D = 0$
Готовые работы на аналогичную тему
$\overline
Переписав уравнение через проекции, получим
Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.
Определить плоскость в пространстве можно и другими способами, например, с помощью указания координат трех ее точек, не лежащих на одной прямой, двух неколлинеарных векторов и точки и т.д. Однако форма записи с помощью нормального вектора плоскости и точки наиболее компактна. К ней другие методы задания плоскости можно привести путем алгебраических преобразований.
С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.
Для начала найдем коэффициенты, соответствующие координатам:
Подставим значения в формулу:
После стандартных преобразований получим ответ:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 03 2021
Нормальный вектор плоскости, координаты нормального вектора плоскости.
Хорошее представление о прямой линии начинается с момента, когда вместе с ее образом одновременно возникают образы ее направляющих и нормальных векторов. Аналогично, при упоминании о плоскости в пространстве, она должна представляться вместе со своим нормальным вектором. Почему так? Да потому что во многих случаях удобнее использовать нормальный вектор плоскости, чем саму плоскость.
В этой статье мы сначала дадим определение нормального вектора плоскости, приведем примеры нормальных векторов и необходимые графические иллюстрации. Далее поместим плоскость в прямоугольную систему координат в трехмерном пространстве и научимся определять координаты нормального вектора плоскости по ее уравнению.
Навигация по странице.
Нормальный вектор плоскости – определение, примеры, иллюстрации.
Для хорошего усвоения материала нам потребуется хорошее представление о прямой в пространстве, представление о плоскости и определения из статьи векторы – основные определения.
Дадим определение нормального вектора плоскости.
Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.
Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если 
— нормальный вектор плоскости 
, то вектор 
при некотором ненулевом действительном значении t также является нормальным вектором плоскости (смотрите статью условие коллинеарности векторов).
Также следует заметить, что любой нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, перпендикулярной к этой плоскости.
Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.
Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.
Приведем пример нормального вектора плоскости.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.
Общее уравнение плоскости вида 
определяет в прямоугольной системе координат Oxyz плоскость, нормальным вектором которой является вектор 
. Таким образом, чтобы найти координаты нормального вектора плоскости нам достаточно иметь перед глазами общее уравнение этой плоскости.
Рассмотрим несколько примеров.
Найдите координаты какого-либо нормального вектора плоскости 
.
Плоскость задана уравнением 
. Определите координаты ее направляющих векторов.
Нам дано неполное уравнение плоскости. Чтобы стали видны координаты ее направляющего вектора, перепишем уравнение в виде 
. Таким образом, нормальный вектор этой плоскости имеет координаты 
, а множество всех нормальных векторов запишется как 
.
Уравнение плоскости в отрезках вида 
, как и общее уравнение плоскости, позволяет сразу записать один из нормальных векторов этой плоскости – он имеет координаты 
.
В заключении скажем, что с помощью нормального вектора плоскости могут быть решены различные задачи. Самыми распространенными являются задачи на доказательство параллельности или перпендикулярности плоскостей, задачи на составление уравнения плоскости, а также задачи на нахождение угла между плоскостями и на нахождение угла между прямой и плоскостью.
Нормальный вектор плоскости, координаты нормального вектора плоскости
Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
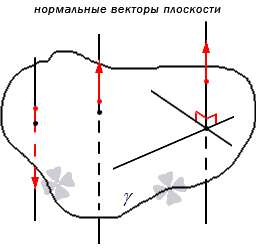
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
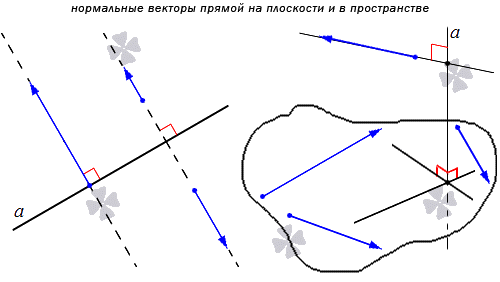
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
Для решения можно выбирать любой удобный способ.
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
Нормальное уравнение плоскости
В данной статье мы рассмотрим нормальное уравнение плоскости. Приведем примеры построения нормального уравнения плоскости по углу наклона нормального вектора плоскости от осей Ox, Oy, Oz и по расстоянию r от начала координат до плоскости. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
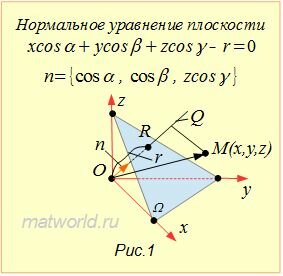
Пусть в пространстве задана декартова прямоугольная система координат. Тогда нормальное уравнение плоскости Ω представляется следующей формулой:
где r− расстояние от начала координат до плоскости Ω, а α,β,γ− это углы между единичным вектором n, ортогональным плоскости Ω и координатными осьями Ox, Oy, Oz, соответственно (Рис.1). (Если r>0, то вектор n направлен в сторону плоскости Ω, если же плоскость проходит через начало координат, то направление вектора n выбирается произвольной).
Выведем формулу (1). Пусть в пространстве задана декартова прямоугольная система координат и плоскость Ω (Рис.1). Проведем через начало координат прямую Q, перпендикулярную плоскости Ω, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором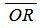 
. (Если точки O и R совпадают, то направление n можно взять произвольным).
 |
Выразим уравнение плоскости Ω через следующие параметры: длину отрезка 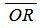и углы наклона α, β, γ между вектором n и осьями Ox, Oy, Oz, соответственно.
Так как вектор n является единичным вектором, то его проекции на Ox, Oy, Oz будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M (x,y, z). Точка M лежит на плоскости Ω тогда и только тогда, когда проекция вектора 
на прямую R равна r, т.е.
Скалярное произведение векторов n и имеет следующий вид:
где 
− обозначен скалярное произведение векторов n и , а | · |− норма (длина) вектора, α−угол между векторами n и .
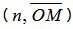
Поскольку n единичный вектор, то (4) можно записать так:
Учитывая, что n=<cosα, cosβ, cosγ>,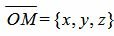 
, мы получим:
Тогда из уравнений (3), (5), (6) следует:
Как было отмечено выше, число r в уравнении (1) показывает расстояние плоскости от начала координат. Поэтому, имея нормальное уравнение плоскости легко определить расстояние плоскости от начала координат. Для проверки, является ли данное уравнение плоскости уравнением в нормальном виде, нужно проверить длину нормального вектора этой плоскости и знак числа r, т.е. если |n|=1 и r>0, то данное уравнение является нормальным (нормированным) уравнением плоскости.
Пример 1. Задано следующее уравнение плоскости:
Определить, является ли уравнение (7) нормальным уравнением плоскости и если да, то определить расстояние данной плоскости от начала координат.
Решение. Нормальный вектор плоскости имеет следующий вид:
 |
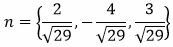Определим длину вектора n:
  |
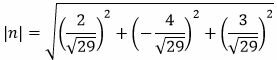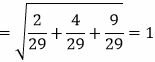Ответ: Длина вектора n равна 1,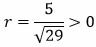 
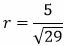
, следовательно уравнение (7) является нормальным уравнением плоскости, а 
− это расстояние плоскости от начала координат.
Приведение общего уравнения плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Утрерждение 2 статьи «Общее уравнение плоскости»), то существует такое число t, что
Возвышая в квадрат первые три равенства в (9) и складывая их, получим:
Упростим выражение и найдем t:
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B, C не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на четвертое равенство в (9). Так как r−это расстояние от начала координат до плоскости, то r≥0. Тогда произведение tD должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку D.
Пример 2. Задано общее уравнение плоскости
Построить нормальное уравнение плоскости (12).
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=6, D=4. Вычислим t из равенства (11):
  . |
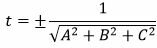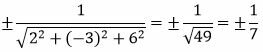Так как D>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 
является расстоянием от начала координат до прямой (12).