Что такое вечная рента

Что такое вечная рента

Определение параметров других рентных платежей

6.7 Вечная рента. Напомним, что под вечной рентой ( perpetuity ) понимается ряд платежей, количество которых не ограничено – теоретически она выплачивается в течение бесконечного числа лет. В практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой абстракции, например, когда предполагается, что срок потока платежей очень большой и конкретно не оговаривается. Примером могут служить некото рые виды облигаций.

Очевидно, что наращенная сумма вечной ренты равна бесконечно большой величине. На первый взгляд представляется бессодержательным и определение современной стоимости та кой ренты. Однако это далеко не так. Современная величина вечной ренты есть конечная величина, которая определяется весьма просто. Выше было показано, что при пределом для коэффициента приведения является . От куда для вечной ренты находим

(6.27)

Таким образом, современная стоимость вечной ренты зависи т только от размера члена ренты и процентной ставки, следует

(6.28)

т.е. член вечной ренты равен проценту от ее капитализирован ной стоимости.

R = 1 получим точное значение: А= 4,999999, а по формуле находим

Для других видов рент получим:

при p > 1, m = 1;

при p = m >1.

Источник

Вечная рента

Вечная рента – это рента с бесконечно большим сроком, а, следовательно, состоящая из бесконечного множества платежей. Вечные ренты используются в страховании, при оценке долгосрочных инвестиций. Оценить можно только современную стоимость вечной ренты. В случае осуществления платежей в конце периода современная стоимость р-срочной вечной ренты будет равна:

(58)

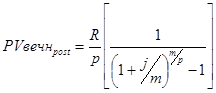
Если платежи осуществляются в начале периода, современная стоимость вечной ренты пренумерандо равна:

(59)

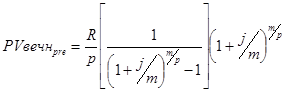
1. Определите сумму необходимую для выкупа вечной ренты, если размеры платежей, которые должны выплачиваться в конце каждого полугодия, равны 500 тыс. руб., а проценты начисляются по номинальной ставке сложных процентов 40% годовых при следующих условиях:

ПЛАН ПОГАШЕНИЯ ДОЛГА

Разработка плана погашения долга заключается в составлении графика периодических платежей должника и определении размеров этих платежей. Эти платежи обычно называют расходы по обслуживанию долга или срочные выплаты (R_t). Расходы по обслуживанию долга включают как текущие процентные платежи (I_t), так и средства, предназначенные для погашения основного долга (C_t).

План погашения долга равными суммами

При составлении плана погашения долга равными суммами подразумевается, что сумма в счет погашения долга (С_t) будет оставаться постоянной величиной на протяжении всего срока и определяется:

(60)

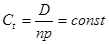
где D – первоначальная сумма долга;

n – срок погашения долга;

p – количество платежей в течение года.

Сумма начисленных за период t процентов (I_t) равна:

(61)

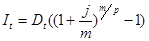
где D_t – остаток долга на период t. В момент первой выплаты D_t = D.

Если оговорено, что выплаты осуществляются в начале периода, а проценты начисляются в конце периода, то в момент первой выплаты проценты еще не начислены, соответственно I₁ = 0.

Cрочная выплата (R_t) за период t:

Остаток основного долга (D_t+1) на период t+1 равен:

1. Долг 50 тыс. руб. необходимо погасить равными суммами в течение 5 лет, взносы осуществляются в конце года. Проценты на долг начисляются по номинальной ставке сложных процентов 20% годовых. Составьте план погашения долга равными суммами.

2. Долг 100 тыс. руб. необходимо погасить в течение 4 лет, осуществляя взносы в начале каждого года. На долг начисляются проценты по номинальной процентной ставке 25% годовых. Составьте план погашения долга равными суммами.

3. Долг 200 тыс. руб. необходимо погасить в течение 3 лет, при этом взносы будут осуществляться в конце каждого полугодия. На долг ежеквартально начисляются проценты по номинальной процентной ставке 20% годовых. Составьте план погашения долга равными суммами.

4. Долг 500 тыс. руб. необходимо погасить в течение 1 года, при этом взносы будут осуществляться в начале каждого квартала. На долг ежемесячно начисляются проценты по номинальной ставке сложных процентов 15% годовых. Составьте план погашения долга равными суммами.

План погашения долга равными срочными выплатами

При составлении плана погашения долга равными срочными выплатами подразумевается, что постоянной составляющей будет являться величина срочной выплаты (R_t) и определяться следующим образом:

— при осуществлении платежей в конце периода:

(64)

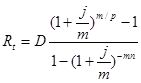
— при осуществлении платежей в начале периода:

(65)

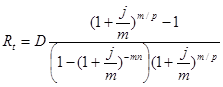
Сумма начисленных за период t процентов (I_t) равна:

(66)

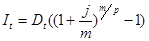
Если оговорено, что выплаты осуществляются в начале периода, а проценты начисляются в конце периода, то в момент первой выплаты проценты еще не начислены, соответственно I₁ = 0.

Cумма в счет погашения основного долга (С_t) за период t:

Остаток основного долга (D_t+1) на период t+1 равен:

1. Составьте план погашения долга равными срочными выплатами, используя условия задач 1 – 4 из п. 9.1.

Источник

Что такое вечная рента

Приведите пример бессрочного аннуитета (вечной ренты). [c.265]

Постоянная вечная рента. Этот вид ренты отличается от предыдущего тем, что постоянный выплаты R производятся вечно, т.е. п = со. Чтобы определить современную величину такой ренты нужно взять предел [c.143]

Вечная рента — см. Бессрочные займы. [c.37]

Материал излагается по уже сложившемуся классическому стандарту. Дается понятие о процентных деньгах, простых и сложных процентах, дисконтировании (учете изменения стоимости денег со временем в связи с возможностью получения процентов), эквивалентности платежей, аннуитетах (сериях регулярных платежей) и вечных рентах. Эти понятия используются для описания элементов практической финансовой деятельности, таких, как оформление векселей и их купля-продажа, амортизация (постоянная выплата) долгов, купля-продажа в рассрочку, образование целевых денежных фондов, расчет инвестиций, оперирование простейшими ценными бумагами-облигациями, определение их рыночной цены, амортизация и обесценивание оборудования, определение цены акций. [c.4]

Глава 7 ВЕЧНАЯ РЕНТА [c.139]

Вечная рента — это аннуитет, платежи которого продолжаются в течение неограниченного срока. Существует много примеров вечных рент возможно, простейшим из них будут платежи процентов от любой суммы денег, инвестированной в производство. Конкретизирующие определения аннуитета, такие, как простой, общий, обыкновенный, отсроченный и т.д., по отношению к вечным рентам имеют тот же смысл, который они имели при описании аннуитетов. Таким образом, обыкновенная простая вечная рента является серией периодических платежей, выплачиваемых в конце последовательных периодов начисления процентов, и должна продолжаться вечно. [c.139]

Нетрудно сразу сообразить, что итоговая сумма вечной ренты не имеет смысла, так как платежи продолжаются неограниченно долго. Однако настоящая стоимость вечной ренты любого типа является конечной суммой, которая может быть быстро найдена, как только будет известна необходимая информация. Для краткости в дальнейшем изложении мы будем опускать в названии вечной ренты слово вечная, понимая всюду под термином рента вечную ренту. [c.139]

Слово капитализация имеет несколько значений. В этой главе оно будет обозначать процесс определения настоящей стоимости серии периодических платежей, которые продолжаются неограниченно долго. Таким образом, капитализировать доход (или расход) при данной норме процента — значит, найти настоящую стоимость вечной ренты, которая будет обеспечивать необходимые платежи. Например, доход в 1 млн руб., полагающийся в конце каждого месяца и капитализированный при трех процентах (т= 12), равен 400 млн руб., так как эта сумма является настоящей стоимостью вечной ренты, которая будет обеспечивать 1 млн руб. в конце каждого месяца, если она инвестирована при 12 = 3 %. [c.146]

Решение. Платежи по 1 млн руб. в конце каждого месяца образуют общую ренту. Если R является платежом эквивалентной простой вечной ренты, тогда [c.147]

Если первоначальная стоимость С является такой же, что и стоимость замены, вычисление можно немного упростить путем рассмотрения первоначальной стоимости, как первого платежа полагающейся вечной ренты. Следующий пример иллюстрирует эту возможность. [c.148]

Привилегированные акции подобны бессрочным облигациям в том, что как те, так и другие являются типами ценных бумаг с фиксированным доходом без дат погашения. Таким образом, цена привилегированных акций Р должна быть равной настоящей стоимости будущих дивидендов F (или постоянных купонов), то есть дивиденды или купоны образуют бессрочный аннуитет (вечную ренту), так что (см. формулу (1) в главе 7) [c.236]

Но хотя при установлении вечных рент или даже при весьма долгосрочных арендах может быть полезно различать между реальной и номинальной ценой, такое различение не имеет практического значения при покупках и продажах, этих наиболее распространенных и обычных сделках в человеческой жизни. [c.106]

Полученное выражение применяется при расчете современной стоимости вечной ренты, о чем пойдет речь в 5.5. [c.108]

Воспользуемся формулой (5.14) для определения взаимосвязи коэффициентов приведения ограниченной и вечной рент [c.108]

В последней записи искомый коэффициент приведения определен как доля коэффициента приведения вечной ренты, зависящая от срока ренты. [c.108]

Не менее просто получаются формулы для кратных бессрочных (вечных) рент. Текущая стоимость единичной /г-кратной обыкновенной бессрочной ренты выражается в виде [c.460]

Стоимость обыкновенной единичной вечной ренты равна 20. Найти стоимость отложенной на 5 лет единичной авансированной вечной ренты. [c.490]

Пример. Годовой фиксированный дивиденд по привилегированной акции равен 60 ден. ед. Найти стоимость этой акции (приведенную стоимость вечной ренты), если дисконтная ставка составляет 20 %. [c.100]

Акции. Поскольку срок действия акции не ограничен, предположив, что дивиденд за каждый год является постоянным и равным Д в абсолютном выражении, можно для определения стоимости акций испОльт зовать модель вечной ренты. В этой модели член ренты R = Д, тогда стоимость акций [c.150]

Когда впервые описывались общие аннуитеты, отмечалось, что их можно анализировать путем замены данной нормы процента на эквивалентную ей норму, согласованную с частотой платежей. Таким образом, общие аннуитеты становились простыми аннуитетами. Однако недостаток такого подхода в том, что новая норма обычно оказывается нетабулируемой и появляются трудности в оценивании функций составных платежей аннуитета. Так как оценивание простой ренты не требует знания функций составных платежей, этот недостаток исчезает. Следовательно, другой способ анализа общих вечных рент заключается в том, что общая вечная рента преобразуется в простую вечную ренту заменой данной нормы процента на [c.144]

По количеству членов различают ренты с конечным числом членов, или ограниченные ренты (их срок заранее оговорен), и бесконечные, или вечные ренты (perpetuity). С вечной рентой встречаются на практике в ряде долгосрочных операций, когда предполагается, что период функционирования анализируемой системы или срок операции весьма продолжителен и не оговаривается конкретными датами. В качестве вечной ренты логично рассматривать и выплаты процентов по бессрочным облигационным займам. [c.96]

Вечная рента. Напомним, что под вечной рентой (perpetuity) понимается ряд платежей, количество которых не ограничено — теоретически она выплачивается в течение бесконечного числа лет. В практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой абстракции, например, когда предполагается, что срок потока платежей очень большой и конкретно не оговаривается. Примером могут служить некоторые виды облигаций (см. гл. 11). [c.122]

Источник

МСФО, Дипифр

Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)

В современном мире, где банковские продукты входят в жизнь любого человека, понимание сути финансовой математики и умение делать простые финансовые вычисления становится необходимым навыком. Но многие учебники и статьи по этой теме написаны сложным языком финансовых терминов и математических формул. Без терминов и формул, конечно, не обойтись. Однако объяснить суть вычислений можно простым языком, понятным любому человеку. Эта статья — продолжение статьи о дисконтировании денежных потоков. В ней речь пойдет об аннуитете (аннуитетных денежных потоках). Вечная рента, формула аннуитета — расчет текущей и будущей стоимости на простых примерах, объяснения для людей, а не для банкиров – об этом вы узнаете, прочитав данную статью.

Что такое аннуитет?

Услышав слово аннуитет, многие подумают о чем-то сверхсложном и недоступном для понимания. На самом деле всё просто, только слово иностранное.

Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Этот термин представляет собой буквенный «перевод» английского слова annuity, что означает «fixed sum paid every year». Люди, владеющие английским языком, вспомнят еще слово «annual», которое в переводе означает «годовой». Оба этих слова происходят от латинского слова annuus – ежегодно. Таким образом, в самом слове аннуитет содержится указание на ежегодную периодичность платежей.

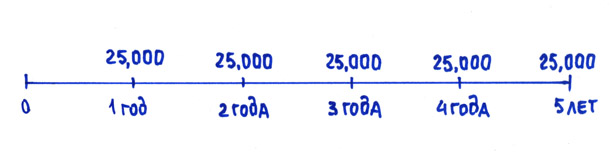
На временной линии (или шкале времени) аннуитетные денежные потоки можно изобразить, например, вот так (Рис. 1):

В настоящее же время аннуитетом называются не только серии одинаковых годовых платежей, но и любые последовательности одинаковых по сумме платежей вне зависимости от их периодичности. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Главным остаётся одно: аннуитет – это несколько одинаковых платежей (денежных потоков) через одинаковые промежутки времени. Например, зарплата. Если ваша зарплата постоянна в течение года, то ежемесячный приток денежных средств в виде зарплаты является аннуитетом с ежемесячным периодом выплаты. Другой пример: если вы покупаете какую-то вещь в рассрочку, то ваши ежемесячные платежи банку тоже будут аннуитетом.

Пренумерандо и постнумерандо

Еще немного терминов. Аннуитеты бывают пренумерандо и постнумерандо. Это красивые и загадочные термины обозначают всего лишь момент платежа: пренумерандо означает платежи в начале каждого временного периода, постнумерандо — в конце его. Эти термины, пришедшие к нам, судя по всему из латыни, используются в учебниках или в официальных бумагах. Я же буду говорить по-русски: денежные потоки с выплатой в конце года или в начале года.

В данной статье рассматриваются примеры расчета простых аннуитетов, в которых период платежа и период начисления процентов равны друг другу. То есть если проценты начисляются, например, за год, то и выплаты будут ежегодными. Или проценты начисляются ежемесячно, и платежи тоже осуществляются ежемесячно. Существуют аннуитеты, в которых эти периоды не совпадают (периоды выплат и периоды начисления процентов), но это более сложные вычисления. Я не буду их затрагивать. Всем, кто хочет разобрать эту тему досконально, лучше обращаться к учебникам по финансовой математике.

Дисконтирование и наращение

Для начала вспомним о том, что такое дисконтирование и наращение. Более подробно об этом рассказано в предыдущей статье. В ней речь шла о дисконтировании и наращении единичного денежного потока, то есть одной денежной суммы. Продисконтировать – это значит рассчитать текущую стоимость будущего денежного потока. То есть, если вам надо накопить определенную сумму к какой-то дате в будущем, то, применив дисконтирование, вы сможете рассчитать, сколько надо положить в банк сегодня.

Наращение – это движение из сегодняшнего дня в завтрашний: расчет будущей стоимости тех денег, которые у вас есть сегодня. Если вы положите деньги на банковский счет, то, зная банковскую ставку, вы сможете рассчитать, сколько денег у вас накопится на счете в любой момент времени в будущем.

Наращение и дисконтирование, конечно, неприменимы, если вы храните деньги дома. Все эти расчеты справедливы только тогда, когда вы можете инвестировать ваши деньги: положить на банковский счет или купить долговые ценные бумаги.

Дисконтирование и наращение применяются не только к одному денежному потоку, но и к последовательности денежных потоков, при этом денежные суммы могут быть любыми по величине. Частным случаем таких множественных денежных потоков и являются аннуитеты.

Формула аннуитета

Аннуитетные денежные потоки тоже можно дисконтировать и наращивать, то есть определять их текущую и будущую стоимости.

Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег. Не зная основных положений финансовой математики, можно прогадать и выбрать заведомо невыгодный для себя вариант. Чем и пользуются более осведомленные участники финансового рынка, а именно банки.

Расчет аннуитета — дисконтирование

ПРИМЕР 1. Возьмем абстрактный пример. Допустим, вам надо выбрать, что лучше:

В сумме 5 * 25,000 = 125,000, что вроде бы лучше, чем 100,000 долларов. Но так ли это? Ведь у денег есть еще и «временная» стоимость. Банковская ставка в данный момент в данной стране, допустим, равна 10%.

Вариант (Б) представляет собой простой вариант аннуитета. Только не все знают, что это именно так называется. Чтобы сравнить эти два варианта между собой (что выгоднее?), надо привести их к одному моменту времени, поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость. Если дисконтированная стоимость аннуитета будет больше, чем 100,000 долларов, значит, второй вариант выгоднее при данной ставке процента.

В предыдущей статье мы научились дисконтировать одиночную сумму. Те же вычисления можно сделать и в этот раз, только придется повторить их 5 раз.

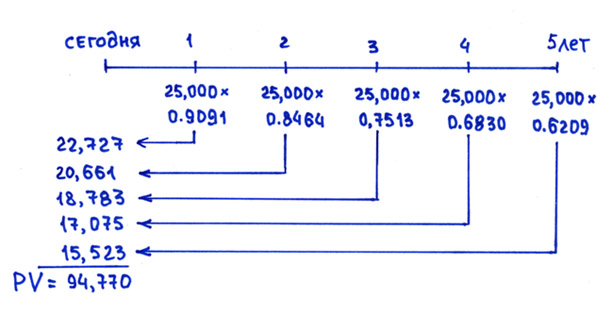
На данной шкале времени кроме платежа в сумме 25,000 нанесены соответствующие каждому периоду коэффициенты дисконтирования. Таблица коэффициентов дисконтирования приведена в предыдущей статье про дисконтирование.

Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая табличка:

Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В целом пять платежей по 25,000 в конце каждого года с учетом дисконтирования стоят 94,770, что несколько меньше, чем 100,000 сегодня. Следовательно, 100,000 сегодня при ставке 10% будет выгоднее, чем предложенный аннуитет 5 лет по 25,000.

Этот пример важен не только, чтобы еще раз продемонстрировать временную стоимость денег. Из таблицы становится ясно, как можно упростить вычисление дисконтированной стоимости аннуитета. Вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз:

25,000*(0,9091+0,8264+0,7513+0,6830+0,6209) что аналогично 25,000*3,7908=94,770

Из этого примера легко вывести математическую формулу расчета дисконтированной стоимости аннуитета.

Сначала вспомним, как выглядит формула дисконтирования:

Коэффициент дисконтирования равен 1/(1+R) n — это 0,9091, 0,8264 и т.д. в нашем примере.

Формула аннуитета (для расчета дисконтированной стоимости аннуитетных денежных потоков)

PV = FV*[1/(1+R) 1 + 1/(1+R) 2 + 1/(1+R) 3 + 1/(1+R) 4 +1/(1+R) 5 ]

И так далее, в зависимости от того, сколько у вас периодов времени.

Выражение в квадратных скобках можно представить математически, но вряд ли это нужно большинству людей. Это называется коэффициент аннуитета, или аннуитетный коэффициент дисконтирования, точное название не столь важно. В примере выше этот коэффициент равен 3,7908.

Гораздо полезнее уметь пользоваться таблицами таких коэффициентов для расчета приведенной (дисконтированной) стоимости аннуитетного денежного потока. Такие таблицы позволяют быстро решать простые задачи на дисконтирование аннуитетов. Пример такой таблицы дисконтирования приведен ниже:

Если кому-то нужна точная формула аннуитета, точнее формула коэффициента дисконтирования аннуитета, то вот она:

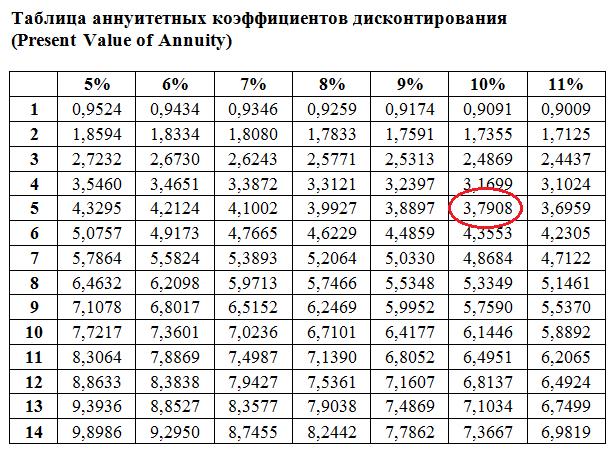
Коэффициент дисконтирования аннуитета: 1/R — 1/(R*(1+R) n )

Дисконтированная стоимость аннуитета: PV= платеж умножить на коэффициент

Расчет аннуитета — наращение

В примере выше мы считали дисконтированную стоимость денежного потока. То есть приводили стоимость денежного потока к текущему моменту времени. Можно решать и обратную задачу – узнать будущую стоимость аннуитета (аннуитетного денежного потока).

ПРИМЕР 2. В нашем первом примере мы можем посчитать будущую стоимость обоих вариантов. Если перевести из области чистой математики в жизненную плоскость, то надо выбрать, что лучше:

Для первого варианта можно воспользоваться таблицей коэффициентов наращения (она есть в предыдущей статье).

Для варианта (Б) ситуация несколько сложнее.

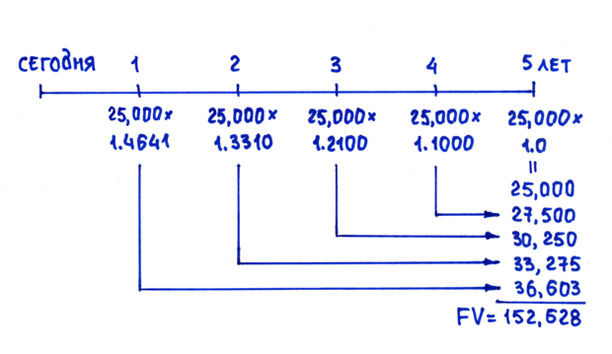
Мы хотим узнать, сколько будет у нас на счете через 5 лет, если мы будем откладывать 25,000 в конце каждого года. То есть мы сделаем последний взнос и сразу же посчитаем, сколько мы накопили. Чтобы не ошибиться, лучше подписать коэффициенты наращения, соответствующие каждому году, на шкалу времени. Первый платеж будет сделан в конце первого года, это значит, что через 5 лет по нему будут наращены проценты только за 4 года. Соответственно, по второму платежу мы получим проценты за 3 года, по третьему – за два года, по четвертому – за один год, и, наконец, положив деньги в пятый раз, проценты по последнему взносу еще нее возникнут (то есть надо будет умножить на 1,10 в нулевой степени!)

25,000*(1,1) 4 +25,000*(1,1) 3 + 25,000*(1,10) 2 + 25,000*(1,10) 1 + 25,000 (1,10) 0 что равно

25,000*1,4641 + 25,000*1,3310 +25,000*1,2100 +25,000*1,1000 + 25,000*1 = 25,000*6,1051 = 152,628

Будущая стоимость аннуитета (вариант Б) равняется $152,628, что существенно меньше, чем $161,050 (вариант А). Это означает, что выгоднее внести на банковский счет 100,000 долларов сегодня, чем делать взносы 25,000 в конце каждого из 5 следующих лет. Данный вывод справедлив для банковской ставки 10% годовых.

Для расчета будущей стоимости аннуитетных денежных потоков тоже имеются таблицы коэффициентов. В данном случае этой таблицей можно пользоваться для расчета аннуитетов с платежами в конце временного интервала (т.е. постнумерандо).

Для любителей математики формула аннуитета для расчета его будущей стоимости выглядит так:

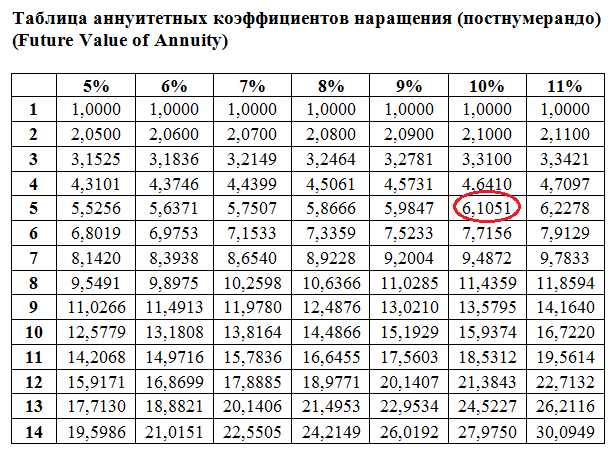
Коэффициент наращения аннуитета: FV = платеж умножить на коэффициент,

где коэффициент равен: [(1+R) n – 1]/R

Это был аннуитет с платежами в конце каждого года (постнумерандо).

ПРИМЕР 3.Можно рассмотреть и другой пример. Сколько мы накопим на счете в банке, если будем вносить по 25,000 в начале каждого года, а не в конце? Это будет так называемый аннуитет пренумерандо, назовем его вариант В. Этот денежный поток можно изобразить на шкале времени таким образом:

Как видно из рисунка, платежи по 25,000 делаются в начале каждого годового периода. Например, вы решили класть на счет в банке по 25,000 каждый год 1 января. Первый платеж принесет нам проценты за 5 лет, второй — за 4 года, третий — за 3 года, четвертый — за 2 год и, наконец, платеж, сделанный в начале пятого года, принесет нам проценты за один год. Коэффициенты наращения я взяла из соответствующей таблицы, которую можно открыть по ссылке.

25,000*1,6105+25,000*1,4641 +25,000*1,3310 + 25,000*1,2100 + 25,000*1,1000 = 25,000* (1,6105+1,4641+1,3310+1,2100+1,1000) = 25,000*6,7156 = 167,890

Таким образом, если начинать вносить 25,000 каждый год в начале годового периода и делать это в течение 5 лет, то через 5 лет сумма на счете будет равна $167,890. Этот вариант В выгодней, чем варианты А и Б, которые были рассмотрены раньше.

Как видно из двух последних примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную или будущую стоимость любых денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.

Как эти расчеты могут пригодиться в жизни?

В примерах выше были разобраны абстрактные примеры аннуитетов. Но с аннуитетными денежными потоками мы встречаемся и в реальной жизни. Например, интересно будет рассчитать, сколько удастся накопить на сберегательном счете, если откладывать каждый месяц часть зарплаты. Подобным же образом можно будет рассчитать, скажем, дисконтированную стоимость всех платежей по автокредиту. Выплаты банку при покупке автомобиля (и не только автомобиля) в кредит представляют собой аннуитет. Его дисконтированная (приведенная к сегодняшнему дню) стоимость — это и будет стоимость приобретаемого автомобиля. Можно точно узнать, сколько вы переплачиваете при покупке машины в кредит в сравнении с вариантом покупки с уплатой полной суммы сразу. А также можно будет сравнить кредитные предложения разных банков. Единственная проблема в таких расчетах – выбрать правильную месячную ставку дисконтирования.

Вечная рента

Вечная рента — это аннуитет, платежи которого продолжаются в течение неограниченного срока. Другими словами – это серия одинаковых платежей, которая продолжается вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.

В викторианскую эпоху все английские аристократы жили на проценты со своего капитала. Чем больший капитал лежал в банке, тем большие средства можно было потратить на жизнь и при этом не работать. Капитал переходил по наследству, и теоретически (если бы не было банкротств банков, войн и инфляции) так могло бы продолжаться вечно.

Будущая стоимость вечной ренты не имеет смысла, так как платежи продолжаются неограниченно долго. Однако текущая стоимость вечной ренты является конечной суммой, которую можно вычислить по формуле:

где R – это банковская ставка %, PV — текущая стоимость

Например, если хочется снимать со счета проценты в сумме 500,000 рублей в год, а годовая банковская ставка составляет 8%, то это значит, что сумма вклада на банковском счете должна быть равна:

500,000/0,08 = 6,250,000 рублей (PV).

В этом случае (если у банка не отберут лицензию или банк не обанкротится сам) можно снимать такие проценты постоянно на протяжении неограниченного периода времени. Единственное, что может нарушить такую идиллическую картину, — это инфляция, благодаря которой деньги обецениваются. Поэтому с течением времени снимаемые проценты будут приносить всё меньше материальных благ.

Философское отступление для тех, кто дочитал до этого места.

Чтобы рента была вечной, нужно сохранять капитал, с которого мы получаем эту ренту. Этот закон действует не только в финансовом мире. Человечество живет за счет природной ренты – оно пользуется ресурсами планеты, которые, к сожалению, исчерпаемы. Если брать от природы слишком много, природная рента иссякнет. Истощение земных ресурсов происходит на наших глазах.

При традиционном рыболовстве рыбу ловили понемногу, но это могло продолжаться вечно. Индустриальные города требуют рыбу определенного сорта и качества, для вылова которой применяется промышленный рыболовный флот. Крупные суда гонятся лишь за прибылью и не уважают океан. В настоящее время 80% мест промысловых районов Европы истощены. По расчетам ученых к 2050 году промышленное рыболовство сойдет на нет. Рыбная «рента» исчерпает себя. Много ли других ресурсов останется у человечества через 35-50 лет?

«Мир достаточно велик, чтобы удовлетворить нужды любого человека, но слишком мал, чтобы удовлетворить человеческую жадность» Махатма Ганди

Планета Земля – это наш единственный дом. Думаем ли мы об этом?

Вы можете почитать другие статьи по данной теме:

Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной, ежедневной, непрерывной) и как рассчитать эффективную ставку по вкладам с капитализацией.

Источник