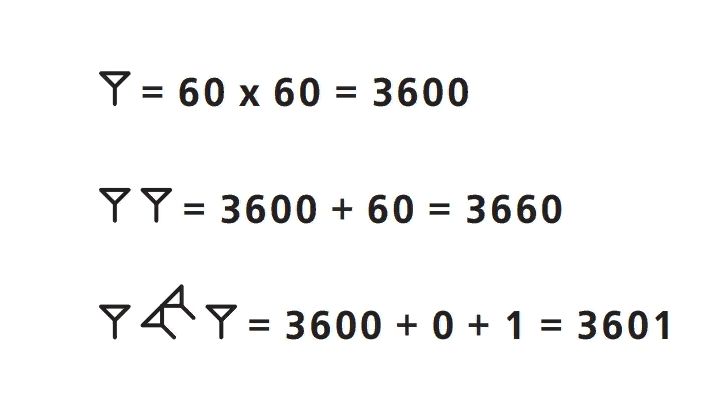Что такое вавилонская система счисления
Вавилонская система счисления
Во сколько вы встали? Под каким углом располагались стрелки часов? Какой ваш знак Зодиака? Некоторые повседневные беседы гораздо древнее, чем мы привыкли думать.
Начнем с 60
Вавилонская система счисления была устроена на базе 10 и 60. Хотя на нее часто ссылаются как на шестидесятеричную, она также использовала 10 в качестве промежуточной точки. Вавилоняне использовали только два символа для записи чисел. Они повторяли символ для единицы (1), пока их не становилось 9, затем использовали другой символ для 10. Они соединяли символы единиц и десятков, пока не добирались до 60, а затем снова использовали символ для 1, сменив его расположение. Это означало, что, комбинируя всего два символа, они могли записать любое число, меняя их положения.
Место для «шестидесятков» использовалось, пока опять не добирались до 59 варианта, затем переходили к следующей позиции; теперь основной символ равнялся 3600.
Секунды и минуты
Деление часа на 60 минут и минуты на 60 секунд пришло из вавилонской системы счисления, хотя вавилоняне не могли так точно измерять время. В круге 360 градусов. Градусы, в свою очередь, делятся на 60 минут, а минуты на 60 секунд. Сейчас, 4000 лет спустя, будет сложно вычеркнуть 60 из нашей системы. Этот неспешный путь, в результате которого эта система прочно внедрилась в новые, вавилоняне не смогли бы вообразить в самых смелых фантазиях. Расширение видимой Вселенной измеряется в гигапарсеках. Определение парсека основано на разделение углов на 360 градусов и подразделениях на 60 минут и 60 секунд.
Почему 60?
Шестьдесят — подходящее число для основания, так как у него много делителей (2, 3, 4, 5, 6, 10, 12, 15, 30). Важный множитель — 12 (60 = 12 х 5), и вавилоняне его тоже широко использовали. То, что начали вавилоняне (а перед ними шумеры), продолжили жители Древнего Египта. Они разбили день на 12 часов — двенадцать в дне и двенадцать в ночи. Часы имели разную протяженность в зависимости от времени года, так как время, когда было светло, разделялось на двенадцать равных частей, и время, когда было темно — на другие (часто отличные) двенадцать равных частей. Первыми, кто решил, что часы должны иметь одинаковую протяженность, были древние греки, но по-настоящему это вошло в употребление только в Средние века с изобретением механических часов. У вавилонян, проживающих рядом с экватором, протяженность часа в течение года радикально не менялась. Возможно, если бы они жили в Финляндии, они бы установили равные часы с самого начала.
Минуты и секунды были введены в 1000 г. н. э. арабским эрудитом Аль-Бируни. Секунду он определил как 1/86 400 среднего солнечного дня. В это время было невозможно точно измерять время, так что минуты и секунды были безразличны большинству людей еще много веков.
Время и пространство
Минуты и секунды используются как для измерения углов в геометрии, так и промежутков времени. Вначале они применялись только для вычисления углов, а их связь со временем появилась из использования сферических приборов для хронометрии.
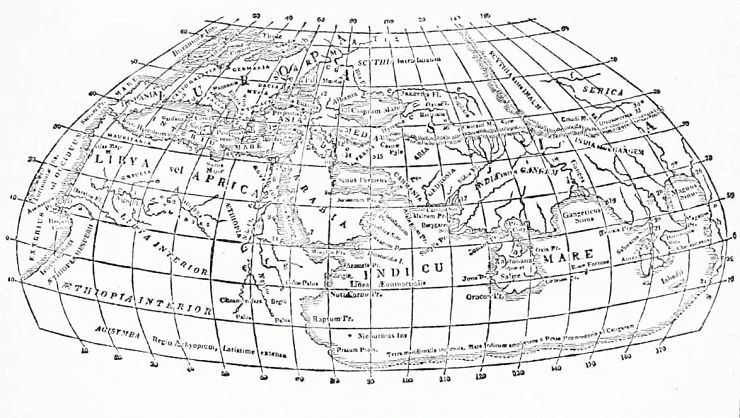
Древнегреческий астроном Эратосфен (ок. 276 — ок. 194 до н. э.) разделил сферу на 60 частей, это была ранняя версия географических широт. Горизонтальные линии проходили через хорошо известные места (хотя на значительно меньшей версии известного ныне мира). Примерно через сто лет Гиппарх добавил систему линий долготы, которые включали 360 градусов и шли с севера на юг, от полюса к полюсу. Еще через 250 лет, около 150 г. н. э., Птолемей разделил каждый из 360 градусов на более мелкие сегменты. Каждый градус был разбит на 60 частей, которые в свою очередь были снова разбиты на 60 сегментов. Термины «минута» и «секунда» произошли от латинского partes minutae primae, или «первая очень маленькая часть», и partes minutae secundae, или «вторая очень маленькая часть.
Половина и четверть часа
В XIV в. циферблат был разделен на часы, но не на минуты. Час делили на четверти и половины, что породило традицию боя часов в эти интервалы. Надежное измерение минут и их повсеместное включение на циферблат пришло в конце XVII в. с изобретением маятника в 1690 г. Поскольку циферблат был круглым, а час уже был разделен на 4 части, решение разбить его на 60 минут было абсолютно оправдано. Это означало, что каждая минута — это 6 градусов, а каждая секунда — 0,1 градуса, хотя понадобится очень большой циферблат, чтобы четко обозначить секунды.
Вавилонская система счисления 🌴: принцип построения и примеры
История вавилонской системы счисления
Даже сейчас историки не знают точно, в результате чего появилась нумерация. Выдвигается много гипотез, однако большую популярность набрали всего две из них.
Версия О. Нейгебауэра
Первое предположение высказал австрийский математик О́тто Эдуа́рд Нейгеба́уэр (1899—1990) — австрийский, позже американский математик и историк науки. Автор глубоких исследований древней и средневековой науки, особенно истории математики.
‘>Отто Нейгебауэр в 1927 году. По его версии исчисление возникло сразу после завоевания древнего Шумера государством, которое называется Аккад. Тогда было введено два денежных номинала, один из которых назывался шекелем, а другой – мина. Историками было установлено, что одна мина была равна шестидесяти шекелям. Спустя некоторое время вавилоняне привыкли к этому представлению и стали использовать её для счета всего остального.
Версия И.Н. Веселевского и другие
Однако эту версию опроверг знаменитый советский математик – Ива́н Никола́евич Весело́вский (1892-1977) — советский механик, математик и историк науки.
Эта версия получила много критики от историков, которые ссылались на то, что в то время нумерацию можно было охарактеризовать как десятичную. Однако в 1985 году французский математик Жор Ифра, в своей работе «Всеобщая история чисел» аргументирует мнение, которое было близко к гипотезе советского ученого.
В докладе говорилось о том, что вавилонская система счисления получилась в результате слияния двух более древних форматов отображения чисел — пятеричного и двенадцатеричного. Это подтверждают и находки археологов, которые показывают, что в то время действительно использовались эти способы представления чисел.
Методы отображения числовых значений
После небольшого экскурса в историю можно перейти к основным определениям, а также рассмотреть, как отображались числовые величины в нумерации древнего Вавилона. Итак
Основные положения в шестидесятеричном исчислении
Вавилонскую систему – можно охарактеризовать, как позиционное счисление по основанию шестьдесят.
Здесь стоит разобрать два слова – «позиционное» и «основание».
Основание – его еще можно охарактеризовать такими словами, как «основа» или «базис». Является количеством знаков, которое использовалось для отображения величин.
Так древние Вавилоняне использовали 60 различных знаков (шестидесятеричное отображение). Их Вы можете увидеть на картинке ниже.
Что касается слова «позиционная», то тут все тоже очень просто. Этот термин говорит о том, что позиция знака (цифры) в числе влияет на его величину. Для примера можно десятичный формат записи, который мы все используем. Так в величинах 5, 50 и 500 цифра пять имеет различный «вес» – в одном случае она обозначает единицы, во втором десятки, ну а в третьем сотни.
Что касается записи, то и она не должна вызывать никаких сложностей. Из изображения выше Вы можете заметить, что для написания знака используются клинышки – одни из них направлены влево, а другие вниз. Именно поэтому этот алфавит называется клинописью. Так клинышки, которые смотрят влево — отображают десятки, а те, что вниз – единицы.
Чтобы разобраться, рассмотрим несколько примеров. Например, 12 в вавилонской системе будет писаться как
А теперь 45
Результаты соответствуют выражениям – 1*10 +2*1=12 и 4*10+5*1=45.
Примечательно, что в этом формате имели представление и большие величины.
Как пример 1972 записывалось вот так
Что равнялось 32*60+52=1972. Аналогия с арабскими цифрами простая – так отсчитав от 0 до 9, мы переходим от разряда единиц к разряду десятков. Также и здесь – посчитав до 60, мы переходим к новому разряду. Получается, что здесь мы считаем не десятками, а значениями, которые кратны 60.
Алгебраические операции и дроби в вавилонской системе
Сложные математические действия, такие как умножение и деление выполнялись с помощью сложных таблиц. Это можно объяснить тем, что использовалось большое количество знаков, и держать числа в уме было очень трудно.
Что касается дробей, то в Вавилоне использовались шестидесятеричные дробные значения (пример 1/60). Используем мы это представление до сих пор в подсчете времени. Так один час равен шестьдесят минут, а минута равняется шестидесяти секундам.
Заключение
Вот и всё, Вы познакомились с вавилонской системой счисления, которая использовалась в древнем Вавилоне. И имеете представление, как её охарактеризовать. Эти знания Вы сможете использовать в своем докладе. Если возникли трудности, то оставляйте вопросы в комментариях к статье.
Вавилонская система исчисления
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
В процессе изучения систем счисления особый интерес представляет так называемая «вавилонская», или шестидесятеричная система счисления, весьма сложная система, существовавшая в Древнем Вавилоне.
Мнения историков по поводу того, как именно возникла эта система счисления, расходятся.
Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое – десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса.
Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60. Отголоски использования этой системы счисления дошли до наших дней. Например: 1 час = 60 минутам, 1° = 60‘.
В целом шестидесятеричная система счисления громоздка.
Системы счисления
Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей.
То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались.
Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.
На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерения или вычислений использовались основания 12 и 60. Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
История появления вавилонской системы счисления
Вавилонская система счисления появилась в Древнем Вавилоне за 2000 лет до н.э. Она очень сильно повлияла на письменность в целом будущего мира.
Вавилонская система (шестидесятеричная) одна из первых известных систем счисления мира, основанная на позиционном принципе. Система счисления Вавилона сыграла огромную роль в развитии математики, астрономии и других точных наук будущего мира, ее следы находят по наши дни.
В наше время мы делим один час на 60 минут, а минуту делим на 60 секунд. Также окружность мы делим на 360 частей. Оказывается теми простыми делениями мы следуем примеру Вавилона!
Для того чтобы определить значения знака, надо было изображение этого числа разбить на разряды справа налево. Чередование групп имеющие одинаковые знаки соответствовало чередованию разрядов. Значение числа определялось по составляющим значениям его цифр, но с тем учетом, что цифры в каждом последующем разряде значили в 60 раз больше тех цифр в предыдущем разряде. В конце числа этот символ обычно не ставился, то есть этот символ не был нулем в нашем понимании.
Таблицу умножения в Вавилоне запомнить было практически невозможно. Вавилоняне пользовались готовыми таблицами умножения при вычислениях. В целом вавилонская система была очень громоздка и неудобна. Эта системы дала очень сильный толчок к развитию будущих систем счисления. Сейчас можно сказать с уверенностью, что если бы не было вавилонской системы счисления, то возможно мы бы сейчас либо пользовались другими системами, либо не могли просто считать.
Особенности вавилонской системы счисления
В Древнем Вавилоне, ок. 1650 до н.э., система счисления была псевдопозиционной или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал ли символ
число 1*(60)2 + 1 или 1*(60)2 + 1*(60), приходилось догадываться из контекста. Однако в период правления селевкидов, ок. 300 до н.э., эта неоднозначность была устранена введением специального символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е. обозначающего пустую позицию в записи числа. Таким образом, из системы счисления была устранена отмеченная выше неоднозначность. Например, символ
означал число 3601, т.е. 1*(60)2 + 0*(60) + 1. В то же время не было найдено ни одной таблички с записью, в которой символ нуля находился бы в конце числа.
Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами позиционной системы счисления с нулем представляло собой огромное достижение, по своему революционному значению для математики сопоставимое разве лишь с более поздней гипотезой Коперника в астрономии.
Символы для обозначения чисел на вавилонских глиняных табличках не столь точны, как символы для обозначения чисел на древнеегипетских папирусах, несмотря на то, что вавилоняне использовали позиционный принцип.
СПИСОК ЛИТЕРАТУРЫ
1. Берман Н.Г. Счет и число. М., 2001.
2. Ван дер Варден Б.Л. Пробуждающаяся наука. М., 1959 Данн-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. СПб.:Питер, 2000.
3. Всевозможные нумерации и системы счисления (http://www.megalink.ru/
5. Юшкевич А.П. История математики, Том 1, М.,1999.
Приложение
Обозначения чисел в Вавилонской системе счисления
Так считали древние. Вавилон
Это продолжение задуманной мной серии про историю вычислений и счета. Первая статья про Египет здесь.
Сейчас я попробую немного рассказать о другой великой цивилизации и культуре прошлого. Вавилонское царство возникло в начале 2-го тысячелетия до нашей эры, оно пришло на смену Шумеру и Аккаду и существовало до завоевания Персами в 539 г. до н.э. Писали в Вавилоне, как все помнят, на глиняных табличках с помощью клинописи, которые очень неплохо сохраняются в отличие от бумаги, папируса, и подобных вещей, поэтому мы знаем достаточно много и про Вавилон, и про его математику. Но, конечно, мы не знаем всего. В отличие от греков вавилоняне не оставили точных алгоритмов и ясных объяснений своих приемов. Теперь мы можем только догадываться как именно вавилоняне действовали в том или ином случае при решении задачи. В этой работе я сосредточусь в основном на вавилонской арифметике, оставив в стороне геометрию, алгебру и астрономию.
Вавилоняне в математике продвинулись намного дальше египтян, насколько нам известно, хотя и не сравнялись с греками, видимо. Они уже умели решать квадратные уравнения, кроме того имели некоторые зачатки числовой алгебры. Одно из их достижений было введение позиционной шестидесятеричной системы счисления без нуля. Это означает, что обращение с числами стало значительно более гибким и простым, чем в Египте. Точно не известно, откуда взялась такая система. Одна из версии говорит, что к ней привело смешение 6-ичной и 10-ичной систем народов Шумера и Аккада. Но существуют и другие мысли на этот счет.
Эта система, к сожалению (может и к счастью, не хотелось бы учить их таблицу умножения) не была освоена другими народами Древнего Мира, и пришлось ждать прихода индийской позиционной системы. Однако, кое-какое отражение вавилонской математики в нашей культуре осталось: деление минуты на шестьдесят секунд и часа на 60 минут — это отзвук древней вавилонской системы счисления.
Цифры и система счисления
На картинке показано, как вавилоняне обозначали 1 и 10. С их помощью изображались все числа от 1 до 59. На картинке ниже показано число 33. Это аналогично римской и другим непозиционным системам записи чисел.
Число 60 обозначалось точно так, как и единица. В начале оно рисовалось крупнее, но позже это различие стерлось. Числа больше 60, но меньше, чем 120 обозначались следующим образом: сначала писалось число 60, потом через пробел остальная часть числа, меньшая 60.
Ниже пример числа 63
Вавилонская система счисления
Вы будете перенаправлены на Автор24
Вавилонская система счисления — это позиционная система счисления с основанием шестьдесят.
Введение
Вавилонская шестидесятеричная система счисления существовала в Древнем Вавилоне. Есть разные мнения по вопросу возникновения этой системы, в частности существуют такие предположения:
В общем, шестидесятеричная система счисления весьма неудобна и громоздка.
Вавилонская системы счисления
Вавилонская система счисления сформировалась в Древнем Вавилоне две тысячи лет до нашей эры. Она оказала сильнейшее влияние на развитие будущей письменности. Шестидесятеричная система счисления является первой известной системой, которая основана на позиционном принципе. Она стимулировала прогресс математических, астрономических и других наук, появившихся позднее.
Доказано, что Вавилонское государство появилось на остатках двух распавшихся империй, Шумера и Аккада. Эти цивилизации оставили после себя большое культурное наследие, которое досталось мудрым вавилонянам. Шумеры оставили им шестеричный числовой код, где имелись в наличии разряды, а аккадцы оставили десятки. Объединение наработок предыдущих поколений, позволило гражданам новой страны создать новую науку, получившую обозначение «математика». Прогресс человеческого общества всё время сопровождался совершенствованием числовой записи, которую нужно было использовать достаточно часто. У различных народностей в разное время применялись разнообразные системы подсчёта. В шестидесятеричной применялись два типа символов. Прямой клин обозначал единицы, лежащий клин служил обозначением десятков. То есть клин в данной системе применяется в качестве цифры. Для обозначения числа шестьдесят применялся такой же прямой клин, как и для единицы. Такой же клин обозначал и все другие числа шестьдесят в разных степенях. Собственно, по этой причине вавилонская система счисления и считается шестидесятеричной. Для определения числового значения конкретного прямого клина, необходимо было написание данного числа разделить на разрядные символы справа налево. Вес числа определялся по сумме его цифровых разрядов, но при учёте правила, что вес цифры в следующем разряде в шестьдесят раз больше предыдущей.
Готовые работы на аналогичную тему
Выучить Вавилонскую таблицу умножения было крайне трудно, вернее фактически невозможно. Поэтому при практических расчётах люди использовали справочные таблицы умножения. В общем шестидесятеричная система достаточно объёмна и применять её для расчётов было не очень удобно. Но она явилась сильнейшим стимулом к появлению в будущем новых систем счисления. Сегодня можно уверенно утверждать, что именно благодаря вавилонской системе мы теперь пользуемся десятичной системой счисления.
Особенности вавилонской системы счисления
Древневавилонская система счисления не была позиционной в полном смысле этого понятия, так как в ней не было аналога сегодняшней десятичной запятой и какого-либо знака (типа ноля), обозначающего отсутствие данного разряда. О конкретном весовом значении символа надо было догадаться из контекста. Но уже во время управления государством Селевкидами (примерно трёхсотые годы до нашей эры), это недоразумение было ликвидировано путём введения особой символики в форме двух клиньев, которые ставились на место отсутствующего разряда в обозначении числа. Но при этом археологи не нашли ни единой записи, где обозначение ноля располагалось бы последним знаком в числе. По этой причине вавилонская система, всё-таки, только относительно позиционная, поскольку символ в крайней правой части числа мог быть обозначением или единицы, или числа, кратного степени шестьдесят. Символика, обозначающая числа на табличках из глины времён древнего Вавилона не такая точная, как на папирусах древнего Египта, невзирая на применение позиционного принципа.
Иногда вавилоняне использовали сокращения при отображении чисел, а иногда применяли новую символику, чтобы обозначить числа сто и тысяча, или пользовались принципами арифметических операций. Преимущество сформированной в Месопотамии системы счисления чётко прослеживается в написании дробей. Тут не нужно было использовать новые символы. Аналогично сегодняшней десятичной позиционной системе, в шестидесятеричной системе имелось ввиду, справа от единиц располагаются числа, которые кратны 1/60, затем 1/602 и так далее.
Для отображения чисел, больших пятьдесят девять древние вавилоняне первыми применили метод, который считается одним из самых больших открытий в числовых системах, это позиционность, то есть зависимость числового веса знака от его расположения в общей структуре числа. Они поняли, что для отображения более старших разрядов возможно использовать уже имеющуюся символику, если она займёт в представлении числа другое местоположение, то есть слева от других знаков. К примеру, знак в виде клина возможно было применять для отображения чисел единица, и шестьдесят, и шестьсот два, и шестьсот три, смотря какое положение он занимал в числовой записи. Аналогично использованию в современных обозначениях единицы в числах 10, и 102 и 103, и в 1111. Когда записывались числа более шестидесяти, символы, которые выступали в новой роли, можно было отличить от уже использованных тем, что они делились согласно «месту», или «позициям», и единицы старших разрядов были расположены слева. При этой методике записи для отображения очень большого числа нет необходимости в применении символики помимо уже используемой.