Что такое вариационные ряды распределения и для чего их строят
Вариационный ряд и методика его составления



Средние величины рассчитываются на основе вариационных рядов.
Вариационный ряд — это однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления.
Цифровое значение, каждого отдельного признака или явления, входящего в вариационный ряд, называется вариантой и обозначается буквой V. Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят названия частот и обозначаются буквой — р. Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой n.
Варианты, расположенные в порядке возрастания или убывания количественной характеристики признака, составляют ранжированный вариационный ряд.
| Вариационный ряд | |||||
| I Виды вариационных рядов | Простой | Сгруппированный | |||
| II Характеристика вариационного ряда | Варианта V | Частота p | Общее число наблюдений n | ||
| III Этапы составления сгруппированного ряда | Определение числа групп | Определение интервала | Определение границ и середины группы | Распределение наблюдений по группам | Графическое изображение |
| IV Практическое применение | Для характеристики типа распределения признака в совокупности | Для вычисления среднего уровня (средней величины) |
Различают два вида вариационных рядов:
— простой вариационный ряд;
— сгруппированный вариационный ряд,
Простым вариационным рядом называется такой ряд, где каждая варианта встречается лишь один раз. Вариационный ряд, где указано сколько раз встречается каждая варианта называется сгруппированным вариационным рядом.
Если исследователь имеет не более 30 наблюдений, то достаточно все значения признака расположить в нарастающем или в убывающем порядке (от минимальной варианты до максимальной или наоборот) и указать частоту каждой варианты. При большом числе наблюдений (более 30) рекомендуется варианты объединить в группы с указанием частоты встречаемости всех вариант, входящих в данную группу.
Основные требования к составлению вариационного ряда:
1. Расположить все варианты по порядку
2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой единицы
3. Определить количество групп
4. Определить интервал между группами
5. Определить начало, середину и конец группы
6. Распределить данные наблюдений по группам
7. Графические изобразить вариационный ряд
Методику построения сгруппированного вариационного ряда рассмотрим на следующем примере:
Даны данные о частоте пульса (число ударов в минуту) у 54 студентов перед экзаменом: 60, 70, 70, 68, 70, 72, 64, 66, 66, 70, 76, 76, 80, 64, 6.2, 78, 78, 76, 70, 68, 64, 62, 70, 68, 72, 70, 72, 72, 70, 70, 76, 76, 76 74, 74, 74, 80, 80, 66, 72, 76, 76, 74, 74, 74, 72, 78, 78, 76, 74, 76, 76, 80, 78.
1. Строим вариационный ряд, последовательно располагая варианты в порядке возрастания: 60, 62, 62, 64, 64, 64, 66, 66, 66, 68, 68, 68, 70, 70, 70, 70, 70, 70, 70, 70, 70, 72, 72, 72, 72, 72, 72,74, 74, 74, 74, 74, 74, 74,76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 78, 78, 78, 78, 78, 80, 80, 80, 80.
2. Распределение студентов в зависимости от частоты пульса перед экзаменом
| частота пульса (V) |
| число студентов (p) |
Всего студентов n =54
3. Определение количества групп.
Количество групп в вариационном ряду находим в специально разработанной таблице.
| Число вариант (n) | 31–45 | 46–101 | 101–200 | 201–500 |
| Число групп (р) | 6–7 | 8–10 | 11–12 | 13–17 |
В нашем примере число наблюдений — 54, поэтому в вариационном ряду следует иметь 8 групп.
3. Определение величины интервала (i) между группами. Интервал между группами определяют по формуле:
| i= | Vmax–Vmin | = | 80–60 | = | =2,5 |
| r (число групп) |
Полученный интервал 2,5 рекомендуется округлять до целого числа — 3.
6. Разбиваем весь ряд на группы используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда
| частота пульса (V) | середина группы вариант | число студентов |
| 60–62 | ||
| 63–65 | ||
| 66–68 | ||
| 69–71 | ||
| 72–74 | ||
| 75–77 | ||
| 78–80 | ||
| n = 54 |
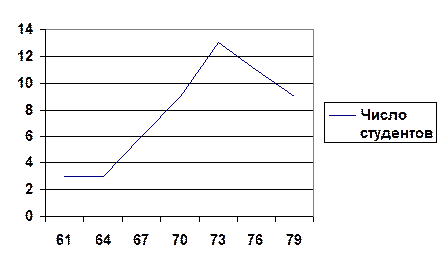
7. Строим графическое изображение вариационного ряда (по серединам групп)
Распределение студентов по частоте пульса перед экзаменом
Полученный ряд распределения (вариационный ряд) и графическое его изображение делают статистические данные обозримыми, доступными для анализа и дальнейшего изучения.
Сводка и группировка статистических данных
3.3. Ряды распределения: виды, правила построения, графическое изображение
Ряды распределения делятся на атрибутивные и вариационные, в зависимости от признака, положенного в основу группировки. Если признак качественный, то ряд распределения называется атрибутивным. Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности (см. табл. 3.1).
Если признак, по которому строится ряд распределения, количественный, то ряд называется вариационным.
Вариационные ряды бывают дискретными и интервальными. У дискретных рядов (табл. 3.7) варианты выражены конкретными числами, чаще всего целыми.
| Время работы в компании, полных лет (варианты) | Число работающих | |
|---|---|---|
| Человек (частоты) | в % к итогу (частости) | |
| до года | 15 | 11,6 |
| 1 | 17 | 13,2 |
| 2 | 19 | 14,7 |
| 3 | 26 | 20,2 |
| 4 | 10 | 7,8 |
| 5 | 18 | 13,9 |
| 6 | 24 | 18,6 |
| Итого | 129 | 100,0 |
Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда. При непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения.
3.3.1. Построение дискретных вариационных рядов
Рассмотрим методику построения дискретных вариационных рядов на примере.
Пример 3.2. Имеются следующие данные о количественном составе 60 семей:
| 2 3 3 1 4 2 3 3 1 5 2 4 3 2 2 1 2 3 4 5 |
| 2 2 1 3 4 3 3 3 6 6 3 3 6 1 3 4 3 4 4 5 |
| 3 3 2 2 1 3 2 5 5 2 4 3 6 1 2 2 3 1 3 4 |
Для того чтобы получить представление о распределении семей по числу их членов, следует построить вариационный ряд. Поскольку признак принимает ограниченное число целых значений строим дискретный вариационный ряд. Для этого сначала рекомендуется выписать все значения признака (число членов в семье) в порядке возрастания (т.е. провести ранжирование статистических данных):
| 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 |
| 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
| 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 |
| Число членов семьи (х) | Число семей (y) |
|---|---|
| 1 | 8 |
| 2 | 14 |
| 3 | 20 |
| 4 | 9 |
| 5 | 5 |
| 6 | 4 |
| Итого | 60 |
3.3.2. Построение интервальных вариационных рядов
Покажем методику построения интервальных вариационных рядов распределения на следующем примере.
Пример 3.3. В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):
| 14,7 | 19,0 | 24,5 | 20,8 | 12,3 | 24,6 | 17,0 | 14,2 | 19,7 | 18,8 |
| 18,1 | 20,5 | 21,0 | 20,7 | 20,4 | 14,7 | 25,1 | 22,7 | 19,0 | 19,6 |
| 19,0 | 18,9 | 17,4 | 20,0 | 13,8 | 25,6 | 13,0 | 19,0 | 18,7 | 21,1 |
| 13,3 | 20,7 | 15,2 | 19,9 | 21,9 | 16,0 | 16,9 | 15,3 | 21,4 | 20,4 |
| 12,8 | 20,8 | 14,3 | 18,0 | 15,1 | 23,8 | 18,5 | 14,4 | 14,4 | 21,0 |
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения.
Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса
Для нашего примера получим: n = 1 + 3,322lgN = 1 + 3,322lg50 = 6,6 » 7.
Для нашего примера
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0.
Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0-14,0; 14,0-16,0; 16,0-18,0; 18,0-20,0; 20,0-22,0; 22,0-24,0; 24,0-26,0.
Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18-25, 26-33, 34-41, 42-49, 50-57, 58-65, 66 и более.
Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.д. записать: до 14,0; 24,0 и выше.
| Ставка банка % (варианты) | |||
|---|---|---|---|
| 12,3 | 17,0 | 19,9 | 23,8 |
| 12,8 | 17,4 | 20,0 | 24,5 |
| 13,0 | 18,0 | 20,0 | 24,6 |
| 13,3 | 18,1 | 20,4 | 25,1 |
| 13,8 | 18,5 | 20,4 | 25,6 |
| 14,2 | 18,7 | 20,5 | |
| 14,3 | 18,8 | 20,7 | |
| 14,4 | 18,9 | 20,7 | |
| 14,7 | 19,0 | 20,8 | |
| 14,7 | 19,0 | 21,0 | |
| 15,1 | 19,0 | 21,0 | |
| 15,2 | 19,0 | 21,1 | |
| 15,3 | 19,0 | 21,4 | |
| 16,0 | 19,6 | 21,9 | |
| 16,9 | 19,7 | 22,7 | |
При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу.
Результаты группировки, полученные в нашем примере, оформим в таблице.
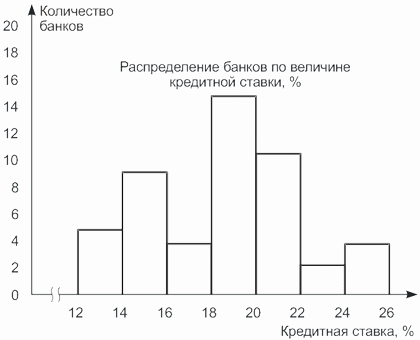
| Краткая ставка, % | Количество банков, ед. (частоты) | Накопленные частоты |
|---|---|---|
| 12,0-14,0 | 5 | 5 |
| 14,0-16,0 | 9 | 14 |
| 16,0-18,0 | 4 | 18 |
| 18,0-20,0 | 15 | 33 |
| 20,0-22,0 | 11 | 44 |
| 22,0-24,0 | 2 | 46 |
| 24,0-26,0 | 4 | 50 |
| Итого | 50 | — |
В процессе группировки данных при построении вариационных рядов иногда используются неравные интервалы. Это относится к тем случаям, когда значения признака подчиняются правилу арифметической или геометрической прогрессии или когда применение формулы Стерджесса приводит к появлению «пустых» интервальных групп, не содержащих ни одной единицы наблюдения. Тогда границы интервалов задаются произвольно самим исследователем исходя из здравого смысла и целей обследования либо по формулам. Так, для данных, изменяющихся в арифметической прогрессии, величина интервалов вычисляется следующим образом:
Порядок расчетов границ неравных интервалов для данных, изменяющихся приблизительно в арифметической прогрессии, показан в табл. 3.15.
Для показателей, приблизительно изменяющихся в геометрической прогрессии, величину интервалов можно вычислить по формуле
Для графического изображения интервального ряда используют гистограмму, имеющую вид многоступенчатой фигуры, состоящей из прямоугольников. По оси абсцисс откладывают значения границ интервалов. Сами интервалы будут являться основаниями прямоугольников. Высота прямоугольников соответствует частоте или частости интервалов, которые откладываются по оси ординат.
По данным таблицы, приведенной в примере 3.3, построим гистограмму (рис. 3.2).
При неравных интервалах у гистограммы распределения высотами прямоугольников будут являться показатели плотности распределения, рассчитываемые как частное от деления частоты интервала на его величину.
Зависимость между значениями признака и накопленными частотами показывают особые графики, называемые кумулятой и огивой распределения.
В случае интервального ряда при построении кумуляты по оси абсцисс отмечают границы интервальных групп, накопленные частоты по оси ординат относят к верхним границам интервалов.
По данным таблицы, приведенной в примере 3.3, построим кумуляту распределения для интервального ряда (рис. 3.2).
Если у кумулятивной кривой поменять местами ось абсцисс с осью ординат, получим график, называемый огивой распределения (рис. 3.4).
Вариационные ряды
| Главная > Учебные материалы > Математика: Вариационные ряды | ||
 | ||
 | ||
| 1.Вариационный ряд. 2.Числовые характеристики вариационного ряда. |
1.Вариационный ряд.
Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1
По данным таблицы построим полигон распределения частот (рис.1)
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2
По данным таблицы построим гистограмму распределения частот (рис.2)
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
2.Числовые характеристики вариационного ряда.
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.
Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.
Пример.
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.
Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).


Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам: