Что такое валидация модели машинного обучения
Валидация моделей машинного обучения
Расширяем понятие валидации
Что не так с валидацией как вычислением одной точечной статистической метрики на отложенной выборке данных?
Аргумент против № 1: одна метрика не может учесть все аспекты качества модели. Качество модели измеряется не только предсказательной способностью, но и, например, стабильностью во времени.
Аргумент против № 2: количественные оценки не всегда согласуются с бизнес-метриками и поэтому вводятся дополнительные. Например, мы можем разработать модель с хорошей интегральной оценкой, но при попытке интерпретации модели в разрезе отдельных факторов может выясниться, что фактор, который по бизнес-логике при увеличении значения должен снижать прогнозный показатель, в разработанной модели, наоборот, его повышает.
Аргумент против № 3: точечная оценка может варьировать в зависимости от состава валидационной выборки, особенно это касается не сбалансированных выборок (с соотношением классов 1:50 или более значимым перекосом). Поэтому стоит дополнительно делать интервальные оценки.
Аргумент против № 4: актуальные данные могут отличаться от исторических, на которых была построена модель, поэтому валидацию стоит делать и на актуальном срезе данных.
Аргумент против № 5: реальные проекты обычно представляют собой набор неоднородных (по сложности и перечню используемых технологий) скриптов, в которых могут быть неточности или неучтенные варианты поведения. Поэтому для корректной работы всего проекта необходимо проводить дополнительную проверку реализации модели, подготавливаемой к развертыванию, причем стоит учитывать не только зависимости между скриптами в проекте, но и порядок их запуска: при несоблюдении порядка они могут отработать без ошибок, но сформировать абсолютно не верный результат.
Валидация и жизненный цикл модели
Профилирование (аудит витрины) осуществляется на этапе подготовки данных. Здесь проверяется соответствие собранных данных поставленной задаче, а также с помощью простых метрик (например, число пропусков в данных, диапазон значений в разрезе отдельных атрибутов) определяется качество витрины.
Когда модель построена, выполняется первичная валидация, чтобы доказать работоспособность и оценить целесообразность внедрения разработанной модели.
Тут может появиться вопрос, чем валидация отличается от мониторинга. Если коротко, то мониторинг — более легковесный процесс, проводимый с большей частотой.
Методика валидации
Все используемые при валидации тесты можно разделить на две группы: количественные и качественные.
Рассмотрим детальнее список тестов для моделей бинарной классификации на примере модели прогноза вероятности дефолта (PD-модели) по кредитному договору (подробнее о PD-моделях см. [1]).
Количественная оценка
К группе относятся расчеты метрик и статистические тесты, которые оценивают качество модели на разных этапах и разных уровнях (перечисляем не все, возможны и другие).
1. Дискриминационная способность модели
После разработки модели первый вопрос, который интересует бизнес-заказчика: а насколько хорошо модель справляется со своей задачей? Если мы построили PD-модель, то этот вопрос звучит так: насколько хорошо модель отделяет клиентов, которые уйдут в дефолт, от тех, кто в дефолт не уйдет, и насколько лучше эта модель, чем случайное угадывание?
где: – число перестановок для валидируемой модели,
– для случайной модели.
Однако, как видно из такой интерпретации, рост коэффициента Джини не всегда означает повышение пользы модели для бизнеса, поскольку не подразумевает изменения в ранжировании в сегменте пользователей, который интересен с точки зрения бизнеса. Ведь при подсчете перестановок не учитываются позиции элементов: на рисунке ниже отображены две возможные модели, которые улучшают базовую на одну перестановку: до порога отсечки и после. Обе модели одинаково улучшат значение метрики Джини, но с точки зрения бизнес-постановки задачи первая модель лучше, так как улучшает ранжирование после порога, среди клиентов, которым будет выдан кредит. Поэтому наравне с Джини нужны другие метрики — о них дальше.
О расчете коэффициента Джини для небинарных целевых событий см. в статье из цикла про риск-моделирование ([3]).
Если выборки не сбалансированы, то используется интервальная оценка с помощью техники бутстрэп. На основе исходной выборки генерируется B (
1000 и более) подвыборок, для каждой из которых рассчитывается коэффициент Джини. Затем проверяется, что заданный заранее перцентиль полученного распределения не пересекает фиксированный порог (например, если 2.5% перцентиль распределения коэффициентов Джини меньше 30%, то по тесту может быть выставлена оценка в виде красного сигнала).
Однако формирование подвыборок с помощью бутстрэпа – вычислительно сложная задача, которая может занять длительное время. С целью ее ускорения используется пуассоновский бутстрэп.
Извлечение с повторением элементов выборки размера n с фиксированной вероятностью можно заменить на сэмплирование с помощью биномиального распределения
частот появления каждого элемента выборки. При условии достаточно большого размера выборки выполняется следующий переход от биномиального распределения к пуассоновскому [4]:
2. Оценка стабильности
Мы разработали модель, проверили ее дискриминационную способность, задеплоили, но спустя несколько месяцев показатели нашей модели ухудшились. После выяснения причин оказалось, что для обучения были отобраны нерепрезентативные данные. Вернемся назад во времени, попробуем предотвратить такую ситуацию и добавим еще один блок в отчет о валидации: стабильность.
где: — доля наблюдений с i-м значением фактора;
— количество наблюдений, соответствующих i-му значению фактора;
— общее количество наблюдений в выборке (
— валидационная выборка,
— выборка для разработки). (Если вы хотите почитать, в каких случаях еще используется PSI, см. например, статью про моделирование компоненты LGD из цикла про риск-моделирование [3].)
Один из способов интерпретации PSI – через дивергенцию Кульбака–Лейблера [5], меру удаленности двух распределений P и Q:
3. Калибровка
Когда мы убедились в стабильности модели, надо проверить, что уверенность модели в сформированных прогнозах соответствует моделируемым значениям целевого события. Для этого применяется калибровка. Здесь мы кратко остановимся на том, как она работает, подробности будут описаны в статье, которая выйдет чуть позже (stay tuned).
Модель считается хорошо откалиброванной, если фактический уровень целевого события (доля наблюдений с фактическим целевым событием = 1) близок к средней прогнозируемой моделью вероятности. Для оценки качества калибровки модели можно проверять попадание наблюдаемого уровня целевого события в доверительный интервал предсказанных моделью вероятностей целевого события: в целом по модели или в рамках бакетов предсказанной вероятности.
Для проверки концентрации используется индекс Херфиндаля–Хиршмана как в целом по выборке, так и в разрезе отдельных сегментов.
Мы перечислили тесты, применимые к моделям в разных доменных областях. Но могут быть метрики, которые отражают специфику конкретного продукта. Например, при моделировании операционных рисков может быть установлено дополнительное ограничение, связанное с пропускной способностью подразделения, проводящего расследования по признанным моделью подозрительными наблюдениям. После того как модель присвоила скоры всем пользователям, топ 1% или 5% пользователей по скору передается для проверки такому подразделению, другие пользователи не будут проверяться. Поэтому необходимо, чтобы максимальное число клиентов с y_true=1 попали в топ 1% или топ 5%.
Также для отдельных моделей могут быть предусмотрены специфические тесты. Например, для LGD-моделей Loss Shortfall.
Качественные тесты
Не все аспекты качества модели можно оценить количественно, поэтому вместе с ними при валидации применяются качественные тесты. Что можно проверять с их помощью?
1. Качество документации модели. Для обеспечения воспроизводимости модели необходима хорошая документация.
Заказчик может дополнительно запросить интерпретацию модели: если это регрессионная модель, то коэффициенты факторов; если decision tree/decision list, то набор правил; если более сложные модели, то отчет интерпретаторов SHAP/LIME.
Эта информация поможет пройти приемку модели, поскольку наглядно показывает, что все важные фичи, на которых модель делает выводы, подкреплены бизнес-логикой.
Model performance predictor (MPP)
В определенных задачах бывает необходимо прогнозировать события, которые произойдут спустя месяцы. Например, клиент не выполнит свои обязательства по кредитному договору в течение года. Из-за этого лага возникает проблема: как понять, что модель стала хуже работать, до того как мы сможем увидеть это, до получения фактических значений целевого события?
Для решения такой проблемы наряду с основной строится дополнительная модель — Model Performance Predictor (MPP) [6].
Схема обучения MPP-модели
Заключение
Бинарное целевое событие:
| Тест | Блок | Виды тестирования по уровню «модель/фактор» | Дополнительные уровни тестирования |
| Джини индекс: абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Предсказательная способность | На уровне модели | По всей выборке / на уровне сегментов |
| IV | Предсказательная способность | На уровне факторов | По всей выборке / на уровне сегментов |
| Тест хи-квадрат | Калибровка | На уровне модели | По всей выборке |
| Биномиальный тест | Калибровка | На уровне модели | По всей выборке |
| Джини индекс: изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| PSI | Стабильность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Стабильность | На уровне факторов | По всей выборке / на уровне сегментов |
| Индекс Херфиндаля–Хиршмана | Концентрация | На уровне модели | По всей выборке / на уровне сегментов |
| VIF | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Парная корреляция | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Значимость факторов (p-value) | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Тест | Блок | Виды тестирования по уровню «модель/фактор» | Дополнительные уровни тестирования |
| Джини индекс (Loss Capture Ratio): абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Корреляция Спирмена: абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| MAE | Калибровка | На уровне модели | По всей выборке |
| Тест Манна–Уитни | Калибровка | На уровне модели | По всей выборке |
| Джини индекс (Loss Capture Ratio): изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| Корреляция Спирмена: изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| PSI | Стабильность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Стабильность | На уровне факторов | По всей выборке / на уровне сегментов |
| VIF | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Парная корреляция | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Значимость факторов (p-value) | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
Материал подготовили: Илья Могильников (EienKotowaru), Александр Бородин (abv_gbc)
Валидация моделей машинного обучения
На связи команда Advanced Analytics GlowByte и сегодня мы разберем валидацию моделей.
Иногда термин «валидация» ассоциируется с вычислением одной точечной статистической метрики (например, ROC AUC) на отложенной выборке данных. Однако такой подход может привести к ряду ошибок.
В статье разберем, о каких ошибках идет речь, подробнее рассмотрим процесс валидации и дадим ответы на вопросы:
Расширяем понятие валидации
Что не так с валидацией как вычислением одной точечной статистической метрики на отложенной выборке данных?
Аргумент против № 1: одна метрика не может учесть все аспекты качества модели. Качество модели измеряется не только предсказательной способностью, но и, например, стабильностью во времени.
Аргумент против № 2: количественные оценки не всегда согласуются с бизнес-метриками и поэтому вводятся дополнительные. Например, мы можем разработать модель с хорошей интегральной оценкой, но при попытке интерпретации модели в разрезе отдельных факторов может выясниться, что фактор, который по бизнес-логике при увеличении значения должен снижать прогнозный показатель, в разработанной модели, наоборот, его повышает.
Аргумент против № 3: точечная оценка может варьировать в зависимости от состава валидационной выборки, особенно это касается не сбалансированных выборок (с соотношением классов 1:50 или более значимым перекосом). Поэтому стоит дополнительно делать интервальные оценки.
Аргумент против № 4: актуальные данные могут отличаться от исторических, на которых была построена модель, поэтому валидацию стоит делать и на актуальном срезе данных.
Аргумент против № 5: реальные проекты обычно представляют собой набор неоднородных (по сложности и перечню используемых технологий) скриптов, в которых могут быть неточности или неучтенные варианты поведения. Поэтому для корректной работы всего проекта необходимо проводить дополнительную проверку реализации модели, подготавливаемой к развертыванию, причем стоит учитывать не только зависимости между скриптами в проекте, но и порядок их запуска: при несоблюдении порядка они могут отработать без ошибок, но сформировать абсолютно неверный результат.
Валидация и жизненный цикл модели
Валидация — комплексный процесс, который осуществляется на протяжении всего жизненного цикла модели. Ее можно декомпозировать на составные части в соответствии с этапами жизненного цикла. На схеме ниже обозначено:
Профилирование (аудит витрины) осуществляется на этапе подготовки данных. Здесь проверяется соответствие собранных данных поставленной задаче, а также с помощью простых метрик (например, число пропусков в данных, диапазон значений в разрезе отдельных атрибутов) определяется качество витрины.
Когда модель построена, выполняется первичная валидация, чтобы доказать работоспособность и оценить целесообразность внедрения разработанной модели.
На этапе внедрения проводится два вида проверок.
Тут может появиться вопрос, чем валидация отличается от мониторинга. Если коротко, то мониторинг — более легковесный процесс, проводимый с большей частотой.
Методика валидации
Все используемые при валидации тесты можно разделить на две группы: количественные и качественные.
В качестве артефакта по результатам валидации предоставляется отчет:
Рассмотрим детальнее список тестов для моделей бинарной классификации на примере модели прогноза вероятности дефолта (PD-модели) по кредитному договору (подробнее о PD-моделях см. [1]).
Количественная оценка
К группе относятся расчеты метрик и статистические тесты, которые оценивают качество модели на разных этапах и разных уровнях (перечисляем не все, возможны и другие).
1. Дискриминационная способность модели
После разработки модели первый вопрос, который интересует бизнес-заказчика: а насколько хорошо модель справляется со своей задачей? Если мы построили PD-модель, то этот вопрос звучит так: насколько хорошо модель отделяет клиентов, которые уйдут в дефолт, от тех, кто в дефолт не уйдет, и насколько лучше эта модель, чем случайное угадывание?
Чтобы ответить на это вопрос, проводим тесты:
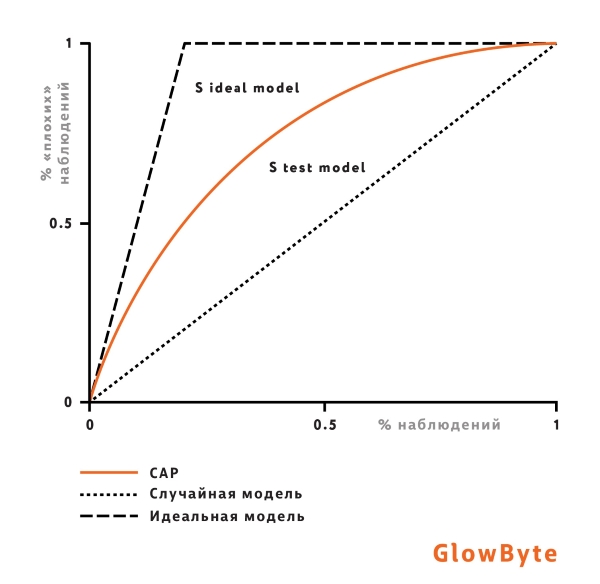
В случае бинарного целевого события коэффициент Джини рассчитывается как отношение площадей двух фигур:
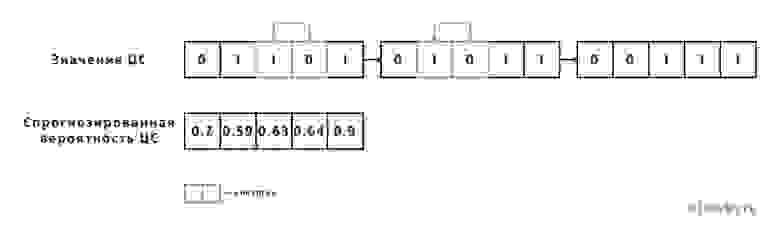
Альтернативный способ определения метрики — пузырьковая сортировка (подробнее см. [2]). Пусть имеется список значений целевого события, порядок в котором совпадает с порядком значений вероятности, прогнозируемых моделью. Тогда показатель Swaps будет обозначать количество перестановок соседних элементов для приведения списка целевых событий к отсортированному виду без инверсий.
На примере ниже число таких перестановок Swaps = 2.
где: – число перестановок для валидируемой модели,
– для случайной модели.
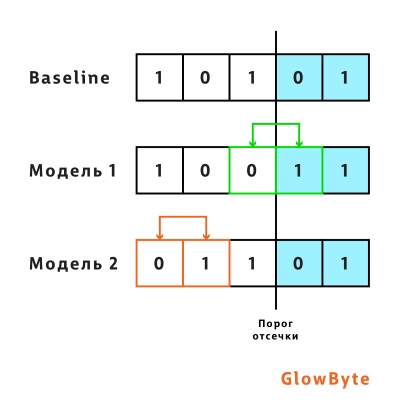
Однако, как видно из такой интерпретации, рост коэффициента Джини не всегда означает повышение пользы модели для бизнеса, поскольку не подразумевает изменения в ранжировании в сегменте пользователей, который интересен с точки зрения бизнеса. Ведь при подсчете перестановок не учитываются позиции элементов. Например, в кредитном скоринге перестановки до порога отсечки по PD с точки зрения бизнеса важнее перестановок после порога отсечки, так как клиенты с высокой вероятностью дефолта в дальнейшем рассмотрении не участвуют. Поэтому наравне с Джини нужны другие метрики — о них дальше.
О расчете коэффициента Джини для небинарных целевых событий см. в статье из цикла про риск-моделирование ([3]).
Если выборки не сбалансированы, то используется интервальная оценка с помощью техники бутстрэп. На основе исходной выборки генерируется B (
1000 и более) подвыборок, для каждой из которых рассчитывается коэффициент Джини. Затем проверяется, что заданный заранее перцентиль полученного распределения не пересекает фиксированный порог (например, если 2.5% перцентиль распределения коэффициентов Джини на уровне одного из факторов модели меньше 3%, то по тесту может быть выставлена оценка в виде красного сигнала).
Однако формирование подвыборок с помощью бутстрэпа – вычислительно сложная задача, которая может занять длительное время. С целью ее ускорения используется пуассоновский бутстрэп.
Извлечение с повторением элементов выборки размера n с фиксированной вероятностью можно заменить на сэмплирование с помощью биномиального распределения
частот появления каждого элемента выборки. При условии достаточно большого размера выборки выполняется следующий переход от биномиального распределения к пуассоновскому [4]:
2. Оценка стабильности
Мы разработали модель, проверили ее дискриминационную способность, задеплоили, но спустя несколько месяцев показатели нашей модели ухудшились. После выяснения причин оказалось, что для обучения были отобраны нерепрезентативные данные. Вернемся назад во времени, попробуем предотвратить такую ситуацию и добавим еще один блок в отчет о валидации: стабильность.
где: — доля наблюдений с i-м значением фактора;
— количество наблюдений, соответствующих i-му значению фактора;
— общее количество наблюдений в выборке (
— валидационная выборка,
— выборка для разработки). (Если вы хотите почитать, в каких случаях еще используется PSI, см. например, статью про моделирование компоненты LGD из цикла про риск-моделирование [3].)
Один из способов интерпретации PSI – через дивергенцию Кульбака–Лейблера [5], меру удаленности двух распределений P и Q:
Мера несимметрична () и из двух срезов данных мы не можем выбрать априорное распределение, с которым будет проводиться сравнение, поэтому для симметричности оценки можно использовать сумму двух мер от P до Q и от Q до P:
Когда мы убедились в стабильности модели, надо проверить, что уверенность модели в сформированных прогнозах соответствует моделируемым значениям целевого события. Для этого применяется калибровка. Здесь мы кратко остановимся на том, как она работает, подробности будут описаны в статье, которая выйдет чуть позже (stay tuned).
Модель считается хорошо откалиброванной, если фактический уровень целевого события (доля наблюдений с фактическим целевым событием = 1) близок к средней прогнозируемой моделью вероятности. Для оценки качества калибровки модели можно проверять попадание наблюдаемого уровня целевого события в доверительный интервал предсказанных моделью вероятностей целевого события: в целом по модели или в рамках бакетов предсказанной вероятности.
Примеры тестов и метрик:
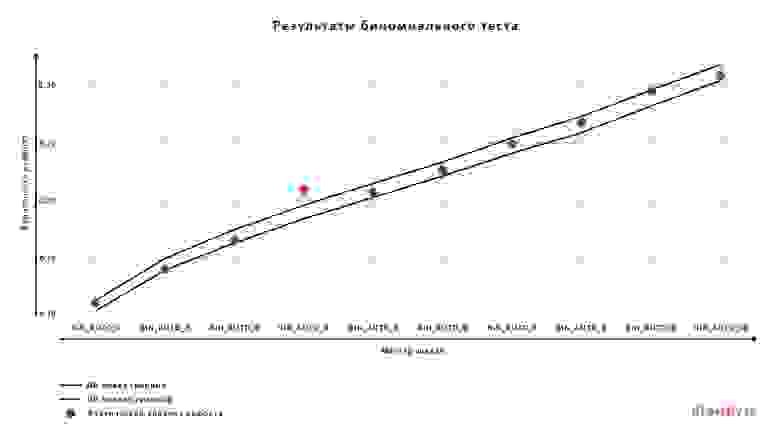
Для проведения биномиального теста диапазон всех вероятностей целевого события разбивается на бакеты по принятой в финансовой организации шкале (мастер-шкале) или по перцентилям. Для каждого бакета рассчитывается доверительный интервал по предсказаниям модели и определяется, попадает ли фактический уровень дефолта в доверительный интервал.
Для формирования итогового решения о стратегии взаимодействия с клиентом может возникнуть необходимость определять разряд по заранее заданной шкале на основе значения вероятности дефолта, спрогнозированного моделью. В таком случае стоит проверить, что в распределении наблюдений по разрядам рейтинговой шкалы отсутствует перекос. Иными словами, чтобы предотвратить попадание большинства всех наблюдений в один-два разряда из всего набора.
Для проверки концентрации используется индекс Херфиндаля–Хиршмана как в целом по выборке, так и в разрезе отдельных сегментов.
Рассчитывается по формуле:
Подводя итог этого раздела, приведем пример пороговых значений метрик валидации моделей бинарной классификации и соответствующие им риск-зоны. В таблице для каждой метрики указаны пороговые значения риск-зон.
Мы перечислили тесты, применимые к моделям в разных доменных областях. Но могут быть метрики, которые отражают специфику конкретного продукта. Например, при моделировании операционных рисков может быть установлено дополнительное ограничение, связанное с пропускной способностью подразделения, проводящего расследования по признанным моделью подозрительными наблюдениям. После того как модель присвоила скоры всем пользователям, топ 1% или 5% пользователей по скору передается для проверки такому подразделению, другие пользователи не будут проверяться. Поэтому необходимо, чтобы максимальное число клиентов с y_true=1 попали в топ 1% или топ 5%.
Также для отдельных моделей могут быть предусмотрены специфические тесты. Например, для LGD-моделей Loss Shortfall.
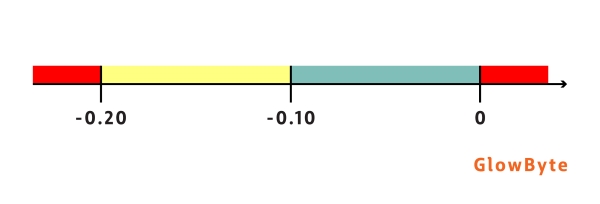
Loss Shortfall – метрика, указывающая, насколько потери от фактического дефолта оказались ниже, чем было предсказано моделью (методика расчета описана в [3]). По шкале выставления оценки для метрики Loss Shortfall видно (см. рисунок ниже), что оценка риска в данном случае производится консервативно, модель считается хорошей только в тех случаях, когда предсказанные потери выше, чем наблюдаемые.
Качественные тесты
Не все аспекты качества модели можно оценить количественно, поэтому вместе с ними при валидации применяются качественные тесты. Что можно проверять с их помощью?
1. Качество документации модели. Для обеспечения воспроизводимости модели необходима хорошая документация.
Оценить качество документации можно, определив, насколько хорошо задокументированы:
2. Дополнительно можно проверить качество использованных при разработке данных:
Заказчик может дополнительно запросить интерпретацию модели: если это регрессионная модель, то коэффициенты факторов; если decision tree/decision list, то набор правил; если более сложные модели, то отчет интерпретаторов SHAP/LIME.
Эта информация поможет пройти приемку модели, поскольку наглядно показывает, что все важные фичи, на которых модель делает выводы, подкреплены бизнес-логикой.
Model performance predictor (MPP)
В определенных задачах бывает необходимо прогнозировать события, которые произойдут спустя месяцы. Например, клиент не выполнит свои обязательства по кредитному договору в течение года. Из-за этого лага возникает проблема: как понять, что модель стала хуже работать, до того как мы сможем увидеть это, до получения фактических значений целевого события?
Для решения такой проблемы наряду с основной строится дополнительная модель — Model Performance Predictor (MPP) [6].
Схема обучения MPP-модели
Для разработки MPP-модели используется тестовая выборка основной модели. Шаги по построению MPP-модели.
Заключение
В завершение сформулируем принципы, которые гарантируют, что валидация модели будет эффективна:
Бинарное целевое событие:
| Тест | Блок | Виды тестирования по уровню «модель/фактор» | Дополнительные уровни тестирования |
| Джини индекс: абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Предсказательная способность | На уровне модели | По всей выборке / на уровне сегментов |
| IV | Предсказательная способность | На уровне факторов | По всей выборке / на уровне сегментов |
| Тест хи-квадрат | Калибровка | На уровне модели | По всей выборке |
| Биномиальный тест | Калибровка | На уровне модели | По всей выборке |
| Джини индекс: изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| PSI | Стабильность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Стабильность | На уровне факторов | По всей выборке / на уровне сегментов |
| Индекс Херфиндаля–Хиршмана | Концентрация | На уровне модели | По всей выборке / на уровне сегментов |
| VIF | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Парная корреляция | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Значимость факторов (p-value) | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Тест | Блок | Виды тестирования по уровню «модель/фактор» | Дополнительные уровни тестирования |
| Джини индекс (Loss Capture Ratio): абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Корреляция Спирмена: абсолютное значение | Предсказательная способность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| MAE | Калибровка | На уровне модели | По всей выборке |
| Тест Манна–Уитни | Калибровка | На уровне модели | По всей выборке |
| Джини индекс (Loss Capture Ratio): изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| Корреляция Спирмена: изменение | Стабильность | На уровне модели | Абсолютное / относительное изменение относительно предыдущего среза |
| PSI | Стабильность | На уровне модели / факторов | По всей выборке / на уровне сегментов |
| Тест Колмогорова–Смирнова | Стабильность | На уровне факторов | По всей выборке / на уровне сегментов |
| VIF | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Парная корреляция | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
| Значимость факторов (p-value) | Дополнительно | На уровне факторов для линейных моделей | По всей выборке |
Материал подготовили: Илья Могильников (EienKotowaru), Александр Бородин (abv_gbc)