Что такое в примере проверка
Математика
Чтобы убедиться, что какое-нибудь арифметическое действие сделано без ошибки, его проверяют.
Проверкой называют совокупность арифметических приемов с целью убедиться, что данное арифметическое действие исполнено верно. Проверка также состоит из арифметических действий, выполненных в другом порядке.
Самый простой способ убедиться, что действие выполнено верно, состоит, конечно, в том, чтобы повторить его снова. Однако, замечено, что уверенность наша увеличивается, если мы убедимся другим путем в верности какого-нибудь результата, поэтому проверяют арифметические действия иначе.
Проверка основана на главных свойствах самих арифметических действий и на зависимости, существующей между данными и искомыми числами.
Основываясь на главных свойствах самих действий, мы можем каждое действие проверять тем же действием, только выполненным в другом порядке. Таким образом, сложение проверяется сложением, вычитание — вычитанием и т. д.
Проверка арифметических действий теми же действиями
Проверка сложения
Сумма не изменяется от перемены порядка слагаемых, следовательно, чтобы проверить сложение, нужно сложить слагаемые в другом порядке; если получится та же самая сумма, сложение сделано верно.
Обычно при проверке складываются слагаемые в обратном порядке, то есть снизу вверх.
Проверка вычитания
Вычитаемое равно уменьшаемому без разности, следовательно, чтобы проверить вычитание, нужно из уменьшаемого вычесть разность; если в остатке получится вычитаемое, вычитание сделано верно.
Проверка умножения
Произведение не изменяется от перемены порядка множителей, следовательно, чтобы проверить умножение, нужно переменить порядок множителей и снова выполнить умножение; если получим то же произведение, умножение выполнено верно.
Проверка деления
При делении нацело делитель равен делимому, разделенному на частное, следовательно, чтобы проверить деление, в случае деления нацело, нужно делимое разделить на частное; если в частном получится делитель, деление сделано верно.
Математика. 2 класс
Конспект урока
Математика, 2 класс. Урок №27
Проверка сложения. Проверка вычитания.
Перечень вопросов, рассматриваемых в теме:
— Что такое обратные математические действия?
— Как проверить сложение?
— Как проверить вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).
Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Обратные действия – действия, приводящие к прежнему, исходному состоянию.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
Теоретический материал для самостоятельного изучения
Используя числа 7, 5, 12 составим все возможные равенства.
Назовём компоненты и результат действия сложения.
Слагаемое + слагаемое = сумма
Назовём компоненты и результат действия вычитания.
Уменьшаемое – вычитаемое = разность
Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.
Как проверить, верно ли выполнено сложение. Воспользуемся знанием того, как связаны слагаемые и сумма. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Это позволяет сложение проверить вычитанием.
Например, надо проверить, верно ли вычислили сумму чисел 28 и 5. Для этого из суммы 33 вычтем одно из слагаемых. Например, 5. Должно получиться другое слагаемое. Получилось 28. Значит, сумма чисел 28 и 5 найдена правильно. Можно вычесть из суммы другое слагаемое.
Сумма чисел 36 и 9 найдена неверно, т.к. после вычитания из суммы 47 слагаемого 9, другое слагаемое, 36 не получается.
Вычислим ещё раз сумму чисел 36 и 9 и проверим результат.
36 – первое слагаемое
Сформулируем правило проверки сложения: «Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно».
Как проверить вычитание? Воспользуемся знанием того, как связаны между собой уменьшаемое, вычитаемое, разность. Если к разности прибавить вычитаемое, то получится уменьшаемое. Значит, вычитание можно проверить сложением.
Вычислим разность чисел 48 и 30. Она равна 18. Проверим вычитание сложением. К разности 18 прибавим вычитаемое 30, получим 48. Это уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Значит, вычитание можно проверить и вычитанием. Рассмотрим это на примере.
Из уменьшаемого 48 вычтем разность 18, получим 30, т.е. вычитаемое. Значит, разность чисел 48 и 30 вычислена верно.
Сформулируем правила проверки вычитания: «Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно», или «Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно».
Вывод: Сложение и вычитание – это обратные действия. Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно. Для того, чтобы выполнить проверку вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.
1. Найдите значение первого выражения в каждой рамке, а затем выполни проверку полученного результата двумя способами.
Мир статистических гипотез
В современном мире мы обладаем все большим и большим объемом данных о событиях, происходящих вокруг. Зачастую у нас появляются вопросы, на которые хотелось бы быстро ответить на основе имеющейся информации, для этого как нельзя лучше подходит процесс, связанный с проверкой статистических гипотез. Однако, многие считают, что это занятие подразумевает под собой большое число вычислений и в принципе довольно сложно для понимания. На самом деле, алгоритм проверки гипотез достаточно прост, а для осуществления расчетов с каждым годом появляется все больше и больше готовых инструментальных средств, не требующих от человека глубоких познаний в области. Далее я попытаюсь показать, что мало того, что процесс проверки гипотез может быть полезным, так и осуществляется достаточно быстро и без серьезных усилий.
Статистические гипотезы и области их применения
Проверка статистических гипотез является важнейшим классом задач математической статистики. С помощью данного инструмента можно подтвердить или отвергнуть предположение о свойствах случайной величины путем применения методов статистического анализа для элементов выборки. Если в предыдущем предложении какие-либо термины являются не совсем понятными, ниже можно найти пояснение на простом языке.
Для проверки статистических гипотез зачастую применяются статистические тесты, о которых будет рассказано далее.
Алгоритм проверки статистической гипотезы
В обобщенном виде алгоритм выглядит таким образом:
Формулировка основной (H0) и альтернативной (H1) гипотез
Выбор уровня значимости
Выбор статистического критерия
Определения правила принятия решения
Итоговое принятие решения на основе исходной выборки данных
Данные шаги являются унифицированными и схему можно использовать почти во всех случаях. Далее подробнее рассмотрим пример работы данного алгоритма на конкретных данных.
Пример проверки статистической гипотезы
Итак, как вы, наверное, догадались по вышеприведенным примерам, будем проверять гипотезу о том, что имеется существенное различие между числом созданных европейских AI-стартапов в 2019-м и 2020-м годах. Пример достаточно простой, чтобы было проще разобраться в ходе работы алгоритма.
Проверка гипотезы о законе распределения
Для данных 2019-го года проверим нормальность распределения.
H0: случайная величина распределена нормально
H1: случайная величина не распределена нормально
Пусть уровень значимости alpha = 0.05 (как и в 95-ти процентах статистических тестов). Определение уровня значимости достойно отдельного поста, так что не будем заострять на нем внимание.
Будет использован критерий Шапиро-Уилка.
,
,
,
;
Можно сравнить статистику W с критическим значением Wкрит. Критическое значение чаще всего приведено в готовых таблицах (по строкам/столбцам там отмечен объем выборки и уровень значимости, а на пересечении как раз-таки и лежит Wкрит.). Если W>Wкрит., то не отвергаем H0 и наоборот. Но это не очень удобно, поэтому чаще используется второй способ.
Разнообразие статистических критериев
Как мы увидели на примере, важным шагом в проверке статистической гипотезы является выбор критерия. В примере выше я использовала лишь два статистических критерия, но по факту их гораздо больше, так сказать, на все случаи жизни. Данные критерии важно знать и четко нужно осознавать, когда и какой можно применить. Многие из них направлены на сравнение центров распределений случайных величин, например, сравнение средних, медиан, равенство параметра распределения какому-либо числу и т. д. В основном они делятся на параметрические (знаем закон распределения случайной величины) и непараметрические.
Для вашего удобства внизу (рис. 3) приведена таблица с основными, с моей точки зрения, критериями сравнения центров распределения и их классификацией. Надеюсь, она будет вам полезна, ее можно дополнять и расширять по вашему желанию.
Как сделать проверку примера столбиком?
Буквенные выражения
Три весёлых поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф приглашают нас с вами, ребята, в гости. Посмотрите, какие дома они построили!
Как вы думаете, можно ли вставить в окошки карточки с цифрами? Почему?
В домике Ниф-Нифа в открытом окошке может быть карточка с цифрой 5? Какое выражение можно записать?
А какое выражение запишем, если в доме Нуф-Нуфа в окошке будет цифра 2?
Можно ли в окошке Наф-Нафа увидеть цифру 1? А цифру 3?
С цифрой 1 запишем выражение: 1 – 1.
А вот цифра 3 не подходит, потому что из 1 нельзя вычесть 3.
Запишите получившиеся выражения и найдите их значения.
Мы записали числовые выражения, ведь они содержат только числа.
Ребята, как вы думаете, можно ли в окошко вставить карточку с буквой?
В математике принято использовать латинские буквы. Может быть, вы уже знаете некоторые из них? Давайте, правильно назовем латинские буквы.
В окошки домиков поросят подставим карточки с буквами: x, y, d.
Запишем выражения: x + 4, 6 + y, 1 – d.
У нас получились буквенные выражения.
Найдём значение следующих буквенных выражений: 8 + а, d – 6, x + 5, y – 1.
Для этого вместо буквы подставим число: а = 12, d = 9, x = 14, y = 20.
Найдите значение выражения: k + 20, если k = 3, k = 5, k = 9.
Видео
Деление дробей в столбик
Разделим 5220 на 36
| — | 5 | 2 | 2 | 3 | 6 |
| 3 | 6 | 1 | 4 | 5 | 36 × 1 = 36 |
| — | 1 | 6 | 2 | 52 — 36 = 16 | |
| 1 | 4 | 4 | 36 × 4 = 144 | ||
| — | 1 | 8 | 162 — 144 = 18 | ||
| 1 | 8 | 36 × 5 = 180 | |||
| 180 — 180 = 0 |
Выделим первое полное делимое 52 Делим 52 на 36. Получится 1 с остатком Под чертой в ответе пишем цифру 1. Проверяем умножением 36х1=36. Вычитаем и сравниваем, разница должна быть меньше делителя. 52-36=16, 16 72 – 30 60 – 20
Различные способы проверки сложения
После того, как пример на сложение решён, его решение можно проверить разными способами. Сложение можно проверить тремя способами: сложением и вычитанием.
Проверка данных в EXCEL
history 26 октября 2012 г.
При вводе большого количества информации в ячейки таблицы легко допустить ошибку. В EXCEL существует инструмент для проверки введенных данных сразу после нажатия клавиши ENTER – Проверка данных.
Инструмент Проверка данных ( Данные/ Работа с данными/ Проверка данных ) не был бы столь популярным, если бы его функциональность ограничивалась бы только собственно проверкой. Ниже кратко перечислены основные приемы работы с этим инструментом.
A. Проверка введенных значений
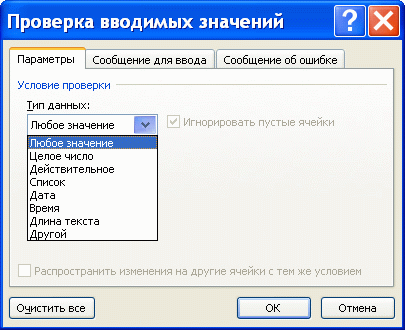
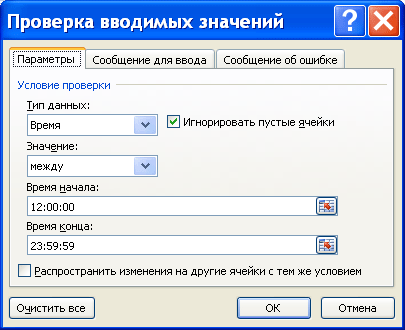
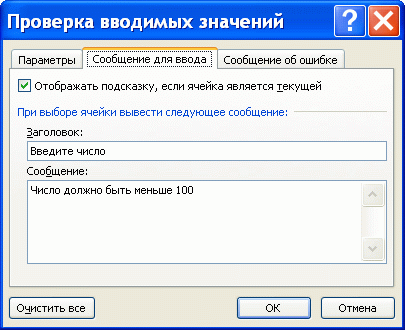
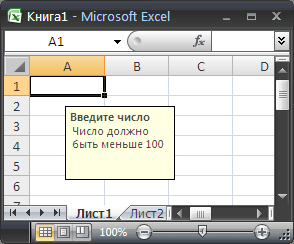
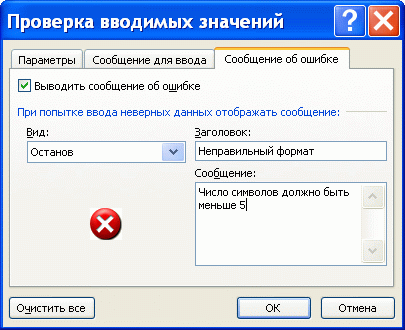
Как видно на рисунке снизу, условия проверки вводимого значения можно настроить очень гибко.
Можно разрешить ввод значений в ячейку только определенного типа, выбрав необходимое условие из выпадающего (раскрывающегося) списка:
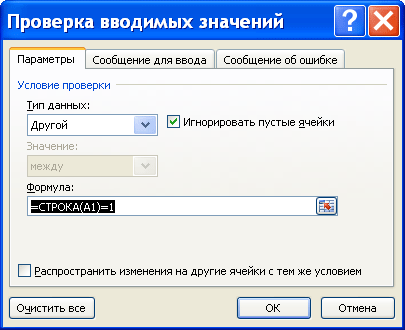
При выбранном типе Другой, в поле Формула нужно ввести формулу для расчета логического значения. Если оно принимает значение ИСТИНА, то такое значение разрешено вводить в ячейку, если ЛОЖЬ, то ваше значение ввести не получится. В качестве аргумента формулы нужно использовать ссылку на саму ячейку, к которой применяется Проверка данных или ссылку на зависящую от нее ячейку. Например,