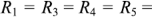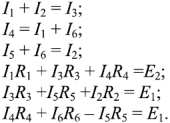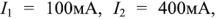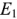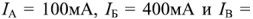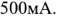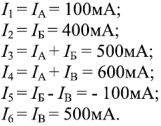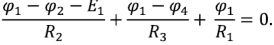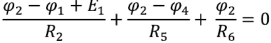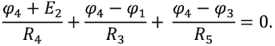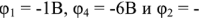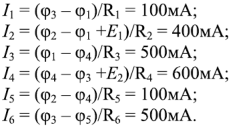Что такое uab в электротехнике

Метод двух узлов

Содержание:

Расчет сложных электрических цепей методом двух узлов

Метод двух узлов применяется в тех случаях, если схема имеет два узла и ряд параллельных ветвей между ними. Для нахождения неизвестных токов составляют уравнения по закону Ома:

где — ток -й ветви;

— ЭДС -й ветви;

— узловое напряжение;

— сопротивление -й ветви;

— проводимость -й ветви, .

ЭДС и напряжение берутся со знаком «+», если их направления совпадают с направлением тока рассматриваемой ветви.

Величина находится по формуле

В этой формуле берется со знаком плюс «+», если ее направление противоположно направлению , и со знаком минус «-», если их направления совпадают.

Пример задачи с решением 1.

Составить необходимые уравнения для определения значений токов в ветвях схемы (рисунок 2.2), используя метод двух узлов.

По закону Ома токи в ветвях:

где

Напряжение между двумя узлами

Рассмотрим применение различных методов на задачах 1 и 2.

Возможно вам будут полезны данные страницы:

Пример задачи с решением 2.

В электрической цепи включены два источника переменного напряжения: (рисунок 4.1). Задачу решить методом контурных токов, методом непосредственного применения законов Кирхгофа и методом узлового напряжения. Осуществить моделирование работы схемы в среде Multisim.

Определить токи в ветвях, если ;

Метод контурных токов.

Определим значение реактивных сопротивлений элементов:

Рассчитаем полные сопротивления отдельных ветвей в комплексной форме:

Тогда исходная схема для решения методом контурных токов преобразуется к виду, представленному на рисунке 4.2.

Определим значения ЭДС источников в комплексной форме:

Система уравнений для определения контурных токов

где

Таким образом,

Находим значение контурных токов:

где

Найти решение системы уравнений в комплексной форме можно, воспользовавшись Калькулятором (рисунок 4.3).

Модель электрической цепи в среде Multisim приведена на рисунке 4.4. Действующие значения токов соответствуют расчётным.

Комплексные мощности источников ЭДС:

Здесь

Комплексные мощности нагрузки

Небольшие расхождения в полученных значениях мощностей объясняются округлением величин при расчете.

Метод непосредственного применения законов Кирхгофа.

Преобразуем заданные комплексные величины из алгебраической формы в показательную:

Записываем уравнение по первому закону Кирхгофа для узла а:

Записываем уравнения по второму закону Кирхгофа:

Объединив уравнения (4.1)-(4.3), получим

В уравнения (4.4) и (4.5) подставляем значения заданных величин:

Решаем уравнения (4.6) и (4.7), используя определители:

Метод узлового напряжения (метод двух узлов).

Размечаем схему применительно к методу узлового напряжения (рисунок 4.5).

Находим комплексные проводимости полных сопротивлений ветвей:

Рассчитываем комплексное межузловое напряжение:

Определяем токи в ветвях:

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Методы расчета сложных электрических цепей

Методы расчета сложных электрических цепей

Сложной электрической цепью называют разветвленную цепь с несколькими источниками электрической энергии. Применение методов эквивалентных преобразований в таких цепях, как правило, не эффективно, так как не позволяют упростить ее до одноконтурной цепи или цепи с двумя узлами. Для расчета таких цепей используют более общие методы.

Метод непосредственного применения законов Кирхгофа

Метод заключается в составлении системы уравнений с применением первого и второго законов Кирхгофа для заданной электрической цени, решение которой позволяет определить токи всех ветвей цепию.

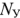
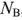
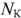
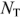
Реализация этою метода, как и любого другого метода расчета сложной электрической цени, начинается с предварительного анализа ее схемы с целью определения числа узлов , числа ветвей , числа независимых контуров , числа ветвей с источниками токов, выяснения возможности упрощения схемы.

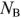
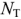
Прежде всего определяют число неизвестных токов, которое равно — . Для каждой ветви задают положительное направление тока.

Далее по первому закону Кирхгофа составляют 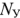— 1 независимых уравнений.

Затем по второму закону составляют 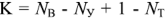уравнений. При этом выбирают независимые контуры, не содержащие источников тока.

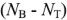
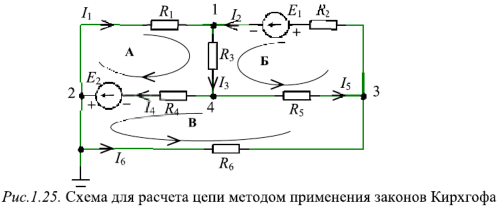
Общее число составленных по первому и второму законам Кирхгофа должно быть равно числу неизвестных токов.

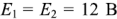
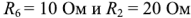
Рассмотрим применение законов Кирхгофа для определения токов в ветвях цепи, схема которой приведена на рис. 1.25. Пусть ЭДС идеальных источников напряжения , сопротивления . Требуется определить все токи схемы с помощью метода непосредственного применения законов Кирхгофа.

Схема содержит 6 ветвей с неизвестными токами и четыре узла. Па схеме узлы обозначены арабскими цифрами, показаны принятые направления токов и направления обхода контуров А, Б и В.

Составим систему из 6 уравнений. Уравнения по первому закону Кирхгофа запишем для узлов 1, 2, 3, уравнения по второму закону Кирхгофа запишем для контуров А, Б, В:

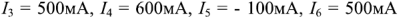
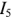
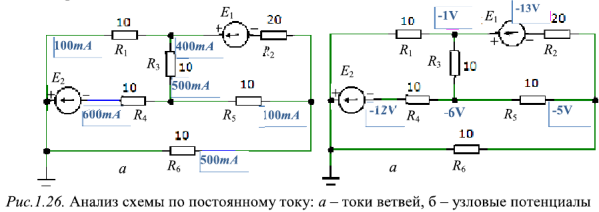
Решив эту систему уравнений, получим . Отрицательное значение тока , указывает на то, что выбранное при составлении уравнений направление этого тока не соответствует действительности. Правильное направление — от узла 3 к узлу 4.

Для проверки вычислений с помощью программы схемотехнического моделирования Micro Сар выполнен анализ по постоянному току схемы, изображенной на рис. 1.25. Изображенные на рис. 1.26,а значения токов ветвей (в мА) подтверждают правильность выполненных расчетов. Изображенные на рис. 1.26,б узловые потенциалы схемы (в В) позволяют определить направление токов ветвей.

Метод контурных токов

Метод контурных токов наиболее часто применяется на практике для расчета сложных цепей, так как он позволяет находить все неизвестные величины при числе уравнений, меньшем числа неизвестных величин.

По этому методу в каждом независимом контуре схемы вместо действительных токов в ветвях вводят условный контурный ток. Действительный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току. Действительный ток в любой ветви, принадлежащей нескольким контурам равен алгебраической сумме контурных токов, проходящих через эту ветвь.

Падение напряжения при прохождении тока смежного контура в элементе принимают положительным, если направление тока в смежном контуре совпадает с направлением обхода, Если направление тока смежного контура не совпадает с направлением обхода, падение напряжения считают отрицательным. Значение ЭДС берется со знаком плюс, если направление обхода контура совпадает с положительным направлением ЭДС, и со знаком минус — если не совпадает.

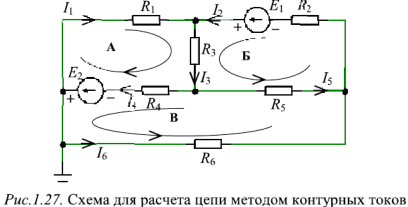
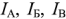
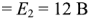
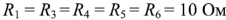
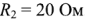
Метод контурных токов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.27. Схема имеет три независимых контура: А, Б, В. Через сопротивления каждого контура проходит свой контурный ток . Направления обхода каждого контура совпадает с направлением контурного тока этого контура. ЭДС идеальных источников напряжения , сопротивления и .

Уравнения, составленные по второму закону Кирхгофа, для контуров А, Б и В:

Подставив в эту систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим

Действительные токи ветвей схемы:

Полученные значения полностью совпадают с результатами ранее проделанного расчета этой же цени по методу непосредственного применения Законов Кирхгофа.

Метод узловых потенциалов

Потенциал любой точки электрической цепи определяется напряжением между данной точкой и точкой цепи с потенциалом равным нулю.

Метод узловых потенциалов заключается в том, что вначале полагают равным нулю потенциал некоторого базисного узла и для оставшихся ( 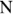-1) узлов составляют уравнения по первому закону Кирхгофа: алгебраическая сумма токов всех ветвей, подключенных к рассматриваемому узлу равна нулю. При этом токи ветвей, соединяющих узлы, определяются с помощью обобщенного закона Ома. Решив полученную систему уравнений, определяют потенциалы узлов.

Далее, применив обобщенный закон Ома для ветвей, определяют искомые токи.

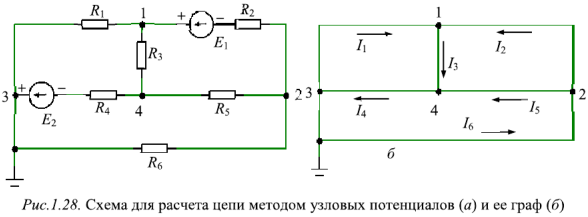
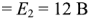
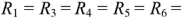
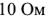
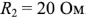
Метод узловых потенциалов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.28 (я). В этой схеме ЭДС идеальных источников напряжения , сопротивления и .

Схема имеет четыре узла. Примем потенциал узла 3 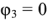. Составляем уравнения по методу узловых потенциалов. Сумма токов узла 1 приравнивается нулю. Ток каждой ветви, подключенной к узлу 1, записывается в соответствии с обобщенным законом Ома

Аналогично для узла 2

Подставив в полученную систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим 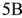. Полученные результаты совпадают с данными (рис. 1.26,6^, полученными при выполнении с помощью программы Micro-Сар анализа по постоянному току схемы, изображенной на рис. 1.28,а.

Применив обобщенный закон Ома для каждой ветви схемы, получим искомые токи:

Полученные значения токов совпадают с результатами расчета этой цепи методом непосредственного применения законов Кирхофа и методом контурных токов.

Направления найденных токов указаны на графе цепи на рис. 1.28,6. Графом цепи называют такое изображение схемы электрической цепи, в котором все ветви заменены линиями, источники напряжения закорочены, а источники тока разомкнуты. Все ветви и все узлы сохраняются.

Метод узловых потенциалов имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа.

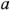
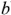
Метод двух узлов является частным вариантом метод узловых потенциалов. Он применяется в тех случаях, когда анализируемая схема содержит только два узла (для определенности узлы и ) и большое число параллельных ветвей, содержащих и не содержащих источники ЭДС. Согласно методу двух узлов межузловое напряжение

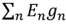
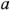
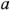
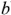
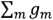
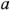
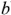
где — алгебраическая сумма произведений ЭДС ветвей (ЭДС считаются положительными, если они направлены к узлу , и отрицательными, если от узла к узлу ) на проводимости этих ветвей; — сумма проводимости всех ветвей, соединяющих узлы и .

Эта теория взята со страницы помощи с заданиями по электротехнике:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Метод двух узлов. Решение задач

Одним из распространенных методов расчета электрических цепей является метод двух узлов. Этот метод применяется в случае, когда в цепи всего два узла.

Алгоритм действий таков:

1 – Примем потенциал узла 2 равным нулю φ₂=0. Тогда напряжение U₁₂ будет направлено из точки с большим потенциалом, к точке с меньшим.

где g₁,g₂,g₃ проводимости ветвей Знак ЭДС определяется её направлением, если к узлу, то положительное, если от узла – отрицательное.

3 – Определим напряжение U₁₂ между узлами

Для общего случая формула напряжения выглядит следующим образом

4 – Найдем токи в ветвях. Причем если направление ЭДС совпадает с направление напряжения, то берем напряжение со знаком плюс. В противном случае со знаком минус.

Как всегда, лучше всего проверить задачу с помощью баланса мощностей. Напомним, что мощность источников ЭДС должна быть равна мощности приемников.

Таким образом, задача решена методом двух узлов. Спасибо за внимание!

Источник