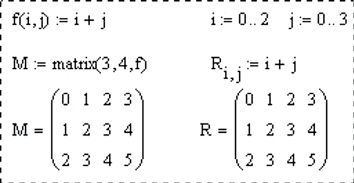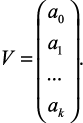Что такое re в маткаде
Что такое re в маткаде
Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
Возвращается.
 x=v.
x=v.Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Научная электронная библиотека
Левинсон Л М, Габдрахманова К Ф, Зиганшин С С,
1.5. Некоторые стандартные функции MathCAD
Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:
M – квадратная матрица;
V – вектор (матрица из одного столбца);
A – произвольная матрица;
S – симметричная матрица;
G – произвольная матрица или число;
X – вектор или число;
Z – комплексная матрица или число;
z – комплексное число;
прочие символы – скалярные величины.
Экспоненциальные и логарифмические функции
exp(X) – экспонента от X;
ln(X) – натуральный логарифм от X;
log(X) – десятичный логарифм от X;
log(X,b) – логарифм от X по основанию b.
Гиперболические и тригонометрические (прямые и обратные) функции
sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;
sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;
asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.
Функции для работы с комплексными числами
Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;
arg(z) – аргумент комплексного числа z (в радианах).
length(V) – возвращает число элементов вектора V;
cols(A) – возвращает число столбцов матрицы A;
rows(A) – возвращает число строк матрицы A;
matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;
identity(n) – единичная матрица n×n;
tr(M) – след матрицы M (сумма элементов главной диагонали);
rank(A) – ранг матрицы M;
norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;
eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;
eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;
cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;
lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.
Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.
Элементы статистического анализа данных
gmean(G1,G2,G3…) – среднее геометрическое аргументов;
mean(G1,G2,G3…) – среднее арифметическое аргументов;
stdev(G1,G2,G3…) – среднеквадратичное отклонение.
fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;
cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;
wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.
Аппроксимация, интерполяция и экстраполяция
Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.
Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).
Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).
Применяются следующие функции MathCAD:
interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;
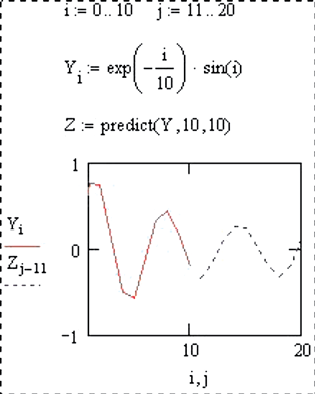
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.
Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.
Примеры интерполяции и экстраполяции:
1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.
1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.
Решения показаны на рис. 19.
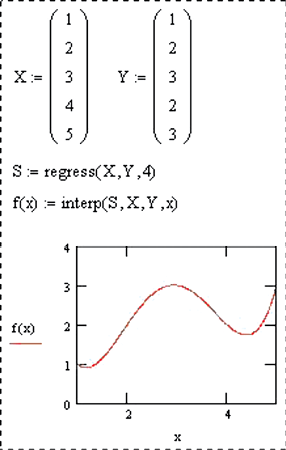
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач
Нахождение корней полинома
max(G1,G2,…) – максимальное значение среди аргументов;
min(G1,G2,…) – минимальное значение среди аргументов;
if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;
sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.
На рис. 20 показан пример применения функции if.
Встроенные операторы и функции Mathcad
Таблица ПЗ.1. Арифметические операторы
Вычитание или отрицание (унарная операция)
Матричное умножение, умножение на скаляр
Скобки (изменение приоритета)
Возведение в степень n
Возведение матрицы в степень n
Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.
Таблица П3.2. Вычислительные операторы
Вычисление n-й производной
Сумма ранжированной переменной
Произведение ранжированной переменной
Таблица ПЗ.З. Встроенные функции по алфавиту
Обратная тригонометрическая или гиперболическая функция *
Функция Эйри первого рода
х,у — координаты точки
Угол между точкой и осью ОХ
file— строковое представление пути к файлу
Дозапись данных в существующий текстовый файл
z — аргумент функции
Аргумент комплексного числа
х,у — координаты точки
Угол, отсчитываемый от оси ОХ до точки (х,у)
А,В,С. — векторы или матрицы
Слияние матриц слева направо
n — порядок х — аргумент
Мнимая и действительная части функции Бесселя —Кельвина
Функция Эйри второго рода
х,у — векторы данных
и — вектор значений сшивок В-сплайнов
n — порядок полиномов
Вектор коэффициентов В-сплайна
Bulstoer (y0, t0, t1, M, D)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера
bulstoer (y0, t0, t1, acc, D, k, s)
Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)
Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)
zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий
хО — левая граница xl — правая граница xf — внутренняя точка
D(x,y) — векторная функция, задающая систему ОДУ
Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке
Наименьшее целое, не меньшее х
Вектор прямого комплексного преобразования Фурье (в разных нормировках)
А — квадратная, определенная матрица
А — матрица или вектор
Объединение строковых переменных
А — квадратная матрица
Числа обусловленности в разных нормах (Ы, L2, Евклидова, »)
А — матрица i — индекс столбца
Сортировка строк матрицы по элементам 1-го столбца
CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)
tO.tl — пределы! sO.sl — пределы s
tgr, sgr — число точек сетки по t и s
fmap— функция преобразования координат
Cre-ateSpace(F[, t0, t1, tgr, fmap])
F(t) — векторная функция из трех элементов
tgr — число точек сетки по t
fmap— функция преобразования координат
Комплексный знак числа
х,у — векторы данных
Вектор коэффициентов кубического сплайна
r,6,z— цилиндрические координаты
Преобразование цилиндрических координат в прямоугольные
х— значение случайной величины
par — список параметров распределения *
Плотность вероятности со статистикой распределения *
Диагональная матрица, на диагонали которой находятся элементы вектора
А — квадратная матрица
Собственные значения матрицы
А — квадратная матрица
А. — собственное значение
Собственный вектор матрицы, соответствующий заданному собственному значению
А — квадратная матрица
Собственные векторы матрицы
Обратная функция ошибок
Возвращает строку S как сообщение об ошибке
Экспонента в степени z
x,y — векторы данных
g — вектор начальных значений а,Ь,с
Вектор прямого преобразования Фурье (в разных нормировках)
Функция Бесселя второго рода нулевого, первого и m-го порядка
n — порядок х — аргумент
Сферическая функция Бесселя второго рода
Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.
Что такое re в маткаде
Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.
Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 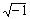
Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.
При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.
Специальные операции над комплексными числами
В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:
Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.
Рисунок 2: Комплексные числа в Mathcad.
При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.
Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.
Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.
Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Что такое re в маткаде
Mathcad содержит функции для выполнения быстрого дискретного преобразования Фурье (БПФ) и его обращения. В Mathcad PLUS имеется также одномерное дискретное волновое преобразование и его обращение. Все эти функции имеют векторные аргументы. При определении вектора v для нахождения волнового преобразования или преобразования Фурье убедитесь, что первый элемент вектора имеет нулевой индекс: v0. Если элемент v0 не определен, Mathcad автоматически устанавливает его равным 0. Это может привести к искажению результата.
Введение в дискретное преобразование Фурье
В Mathcad входят два типа функций для дискретного преобразования Фурье: fft/ifft и cfft/icfft . Эти функции дискретны: они берут в качестве аргументов и возвращают векторы и матрицы. Они не могут быть использованы с другими функциями.
Используйте функции cfft и icfft во всех других случаях.
Первое условие необходимо, потому что функции fft/ifft используют тот факт, что для вещественных данных вторая половина преобразования Фурье является комплексно сопряженной с первой. Mathcad отбрасывает вторую половину вектора-результата. Это сохраняет и время и память при вычислениях.
Пара функций cfft/icfft не использует симметрию в преобразовании. По этой причине необходимо использовать их для комплексных данных. Так как вещественные числа — подмножество комплексных чисел, можно также использовать пару cfft/icfft для вещественных чисел.
Второе условие требуется, потому что пара функций fft/ifft использует высоко эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргумента, используемого с fft, должен иметь 2 m элементов. В функциях сfft/icfft использован алгоритм, который допускает в качестве аргументов как матрицы, так и векторы произвольного размера. Когда эта пара функций используется с матрицей в качестве аргумента, вычисляется двумерное преобразование Фурье.
Обратите внимание, что, если использована функция fft для прямого преобразования, необходимо использовать функцию ifft для обратного. Аналогично, если для прямого преобразования использована cfft, то для обратного необходимо использовать icfft.
Различные формулировки определения преобразования Фурье используют различные нормировочные коэффициенты и соглашения о знаке перед мнимой единицей в показателе экспоненты прямого и обратного преобразований. Функции fft, ifft, cfft и icfft используют 1/ 
Преобразование Фурье в вещественной области
Для вещественнозначных векторов с 2 m элементами можно применять пару функций fft/ifft. В алгоритме вычисления этих функций используются преимущества симметрии, существующей только для вещественных данных. Это позволяет сохранить и время, и память, необходимые для вычислений.
Элементы вектора, возвращаемого fft, вычисляются по формуле
В этой формуле n — число элементов в v, i — мнимая единица.
| ifft (v) | Возвращает обратное дискретное преобразование Фурье; результат — вещественнозначный. |
Аргумент v — вектор, подобный созданному функцией fft. Чтобы вычислить результат, Mathcad сначала создает новый вектор w, комплексно сопряженный v, и присоединяет его к вектору v. Затем Mathcad вычисляет вектор d, чьи элементы вычисляются по формуле:
Это та же самая формула, что и для fft, кроме знака минус в функции exp. Функции fft и ifft — точные обращения. Для всх вещественнозначных v справедливо ifft(fft(v))=v.
Преобразование Фурье в комплексной области
Комплексное преобразование Фурье требует следующих функций:
| cfft (A) | Возвращает дискретное преобразование Фурье комплекснозначных вектора или матрицы. Возвращаемый массив имеет тот же самый размер, что и массив, используемый как аргумент. |
| icfft (A) | Возвращается обращение дискретного преобразования Фурье вектора или матрицы данных. Функция icfft — обратная к функции cfft. Подобно cfft, эта функция возвращает массив того же самого размера, что и аргумент. |
Рисунок 3: Использование быстрых преобразований Фурье в Mathcad.
Пара преобразований cfft/icfft может работать с массивами любого размера. Однако они работают значительно быстрее, когда число строк и столбцов может быть представлено в виде произведения большого количества меньших сомножителей. Например, векторы с длиной 2 m относятся к этому классу, так же как и векторы, имеющие длины, подобные 100 или 120. С другой стороны, вектор, чья длина — большое простое число, замедлит вычисление преобразования Фурье.
Функции cfft и icfft — обратные друг к другу. То есть icfft(cfft(v))=v. Рисунок 3 показывает примеры использования преобразования Фурье в Mathcad.
Когда в качестве аргумента cfft используется матрица, результат есть двумерное преобразование Фурье исходной матрицы.
Альтернативные формы преобразования Фурье
Определения преобразования Фурье, обсужденные выше, не являются единственно возможными. Например, следующие определения для дискретного преобразования Фурье и его обращения можно найти в книге Ronald Bracewells, The Fourier Transform and Its Applications (McGraw-Hill, 1986):
Функции FFT, IFFT, CFFT и ICFFT используются аналогично функциям, обсужденным в предыдущем разделе.
Волновое преобразование
A Mathcad PLUS включены две функции волновых преобразований: для выполнения прямого одномерного дискретного волнового преобразования и его обращения. Преобразование выполняется с использованием четырехкоэффициентного волнового базиса Даубечи.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter