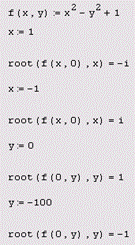Что такое mathcad и для чего он предназначен
Обзор Mathcad. Лучший помощник в вычислениях.
Дорогие друзья. Мы уже вели с вами беседу об опасностях, подстерегающих начинающего математика, физика и инженера. Как бы ни была интересна сама суть науки, для того, чтобы описать эту самую суть, применяется математический аппарат. И вот этот самый аппарат, со своими громоздкими выкладками, приближениями, углами тета фи и кси зачастую уничтожает в студентах всякий интерес к описываемому вопросу. В этой статье мы не будем говорить о том, как подогреть этот интерес, нет. Поговорим о том, как избежать громоздких математических выкладок.
Сразу оговоримся, мы не агитируем за то, чтобы не учиться считать вручную, как раз наоборот. Еще Михаил Васильевич Ломоносов говорил: математику уже затем учить надо, что она ум в порядок приводит. И он был совершенно прав. Кто сомневается – попробуйте!
Тем не менее, современные объемы информации таковы, что зачастую считать вручную бывает просто физически невозможно. Как быть?
Известно как! Ведь мы уже проводили обзор МАTLAB, скажете Вы. Да, все верно, но помимо матлаба, существуют и другие средства. Для общего развития, их полезно знать. Пакеты Mathcad, Maple, Mathematica, Maxima и еще множество других.
Одно из них – пакет Mathсad. Настолько простая и удобная программа, что мы просто не можем обойти ее стороной.
Изначально Mathсad создавался для решения задач не теоретической, а прикладной математики. Т.е. задач, не требующих глубокого внедрения в математическую суть проблемы, а использующих математику лишь как средство решения. Начиная с 14-й версии, в Mathсad используется символьное ядро MuPAD. При этом, в отличие от более мощной программы Maple, символьное ядро Mathсad искусственно ограничено. Тем не менее, 300 доступных функций обеспечивают возможность для решения большого количества задач инженерного характера. В помощь статья как сделать презентацию в powerpoint.
Еще одно выгодное отличие Mathсad – это интерфейс. Ввод данных является графическим, а не текстовым. Что это значит? Это значит, что Вы не набираете формулы каким-то замудренным методом, а записываете их в рабочее поле в совершенно обычном, привычном книжном виде. Используя для этого или клавиатуру, или перетаскивая значки с панелей инструментов Mathсad.
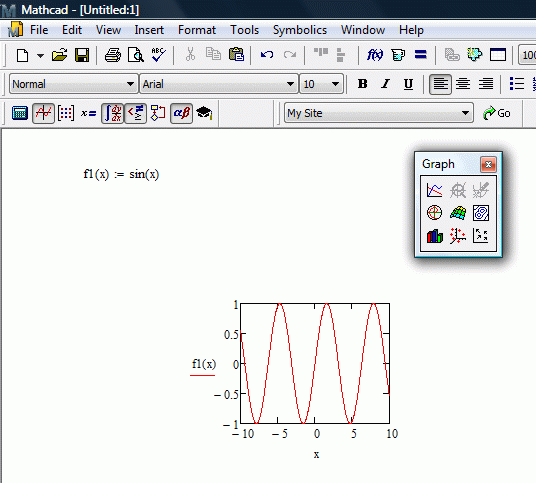
Для примера, расскажем ниже, как задать функцию в маткаде, а затем построить график функции. Пусть это будет простая функция – с простыми функциями все всегда понятнее. Скажем, f(x)=sinx
затем открываем панель Graph, нажимаем X-Y Plot, и выбираем нужный нам вид графика. Оси для удобства можно подписывать самостоятельно, также график можно растягивать и сжимать.
Рассмотрим ниже некоторые возможности маткада на примерах, в контексте самых популярных и часто используемых его функций. Надеемся, данная информация будет полезна начинающим пользователям.
Например, есть общая задача: нужно решить уравнение. Какие способы и встроенные функции предлагает для этого Mathcad? Идем по порядку.
1) Функция root (англ. Root – корень). Данная функция используется для нахождения корней уравнения с одним неизвестным. Запись в Mathcad выглядит следующим образом:
Здесь x – переменная, варьируя значение которой программа будет искать точки пересечения графика y=f(x) с осью абсцисс.
2) Функция find (англ. Find – искать, найти). Известно, что с помощью Mathcad можно решать не только уравнения, но также и уравнения с несколькими переменными, а также системы уравнений, число которых может достигать аж 50-ти. Именно в таких случаях помогает данная функция. При решении системы перед самими уравнениями слудует написать слово given, указывающее программе, что далее соедует система уравнений. Связка given-find возвращает значения переменных, обращающих уравнение в верное тождество. Для случая систем уравнений возвращается в виде вектора. Записывается в виде
А теперь, как это выглядит в рабочем поле маткада, с произвольными значениями
3) Функция minerr. Если функция find позволяет найти только точные значения, то при помощи оператора minerr Вы сможете найти приближенные значения корней уравнения и системы уравнений с равным количеством уравнений и неизвестных. Записывается так:
Minerr(x1, x2, …)
4) На случай решения систем линейных алгебраических уравнений (СЛАУ), когда необходимы операции над матрицами, Mathcad имеет встроенную функцию
Например, представим, что нам нужно решить линейную систему уравнений вида
В матричном виде данная система запишется следующим образом
B- столбец свободных членов.
Именно матрица коэффициентов и столбец свободных членов являются аргументами функции lsolve(A, B), возвращающей вектор-столбец решений СЛАУ.
Надеемся, что данная статья будет полезна начинающим пользователям Mathcad, а также тем, кто только собирается взяться за его освоение. Можно с уверенностью сказать одно: из всех подобных программ, Mathcad обладает явными преимуществами. Простота интерфейса в сочетании с широким набором возможностей делают эту программу популярной как среди зеленых студентов, так и среди состоявшихся ученых мужей мирового масштаба.
Напоследок, несколько слов о системных требованиях. Как уже говорилось, программа многофункциональна, но по мощности уступает своим аналогам. А значит, маткад будет уверенно чувствовать себя на потрепанном стареньком лэптопе. Для успешной установки Вам понадобится:
— 32-х или 64-х битный процессор с тактовой частотой 400 МГц (рекомендовано 700 МГц)
— 256 МБ ОЗУ (рекомендовано 512 Мб)
— 1,75 Гб свободного пространства на диске
— Видеокарта SVGA или выше, монитор, поддерживающий разрешение 1024×768 и выше
Удачи в учебе! И помните, ничего сверхсложного в решении, казалось бы, громоздких задач, нет. Немного усердия, немного практики, и дело пойдет на лад. В принципе, не бывает нерешаемых задач, нужен только верный подход. А если Вам нужна консультация, по любому вопросу смело обращайтесь к нашим специалистам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Mathcad Express — бесплатный математический редактор, про который мало кто знает
Прежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.
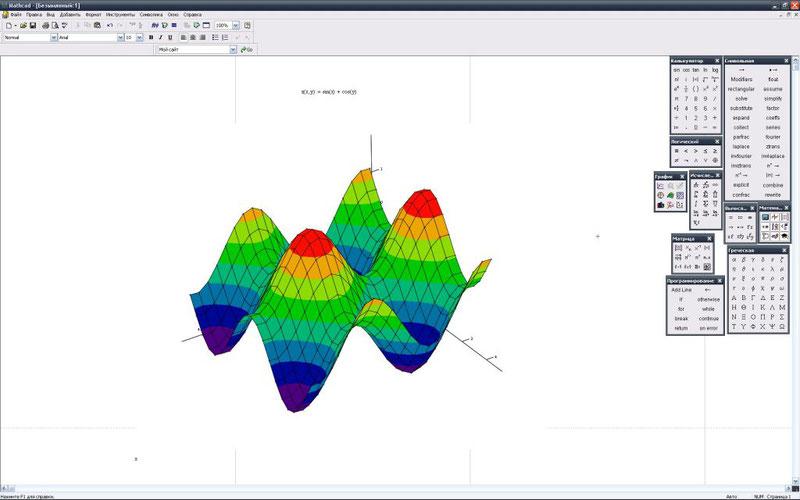
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков. На протяжении последних лет Mathcad стал очень популярным, и его, на мой взгляд, по праву можно считать математическим пакетом №1 в мире.
Сначала несколько фактов о Mathcad, конечно, известных большинству читателей, т.к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века. В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime. Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
Сразу скажу, что русскоязычный дистрибутив, полнофункциональную 30-дневную версию Mathcad Prime вы можете скачать с сайта русского реселлера РТС. Если вы уже собрались попробовать ее в работе, мой совет – не торопитесь в Мастере установки согласиться с включением тестового 30-дневного периода. Дело в том, что Mathcad Prime, наряду с мощной полнофункциональной версией (окно которой вы видите сверху) имеет бесплатную ограниченную версию, которая называется Mathcad Express. Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными. Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Формулы можно вводить в документы либо с клавиатуры (если подходящие символы на ней есть), либо при помощи меню Математика. Давайте ради примера посчитаем интеграл от функции cos(x). Для этого выбираем символ интеграла, а потом — в соответствующие местозаполнители вводим (с клавиатуры) пределы интегрирования и подынтегральную функцию cos(x). Остается нажать клавишу «равно», чтобы сразу получить ответ.
Надо хорошо себе представлять, что происходит, когда мы вводим знак равенства. А именно, запускается соответствующий численный алгоритм вычисления интеграла: интервал интегрирования разбивается на некоторое число отрезков, в определенных точках которых вычисляется массив значений подынтегральной функции, который потом пересчитывается в соответствующую аппроксимацию интегральной суммы. Таким образом, большая часть расчетов скрыта и происходит «за кадром», а на экран выводится лишь конечный результат.
Ключевые инструменты Mathcad – это операторы и функции. Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
Давайте теперь определим пользовательскую функцию f(t), которая будет зависеть от переменной t. Будем использовать предназначенный для этого в Mathcad оператор присваивания (двоеточие со знаком равно).
Мы определили функцию f(t), как наш интеграл от cos(x) с переменным верхним пределом t. После того, как мы определили функцию f(t), можно посчитать ее значения в точках (для чего достаточно ввести аргумент и нажать клавишу «равно», чтобы вывести в документ ответ). Для ввода константы, например π, используется или меню Символы, или меню Константы.
В качестве аргумента можно использовать не только скалярную, но и векторную переменную. Определить ее можно так:
Тогда и результатом вычисления функции будет соответствующий вектор.
Наконец, одна из важных возможностей Mathcad Express – это возможность построения в документе графиков. Давайте выделим место в документе и вставим в это место XY-график (т.е. декартов график) нашей функции f(x).
Обозначаем на оси абсцисс имя переменной z (чтобы не путать с уже использованными ранее x и t), а на оси ординат – имя функции f(z), функцию, которую, как вы помните, мы определили, как интеграл от косинуса, равный конечно, sin(z). В итоге, получаем график этой функции.
Скажу еще, что в Mathcad Express (возможно, по недосмотру разработчика) остаются доступными матричные операции. Поэтому Mathcad Express — довольно мощный инструмент для решения задач линейной алгебры.
Переходя по документу вверх и вниз, мы можем просматривать свои расчеты, а управлять ими можно при помощи меню Расчет. По умолчанию, включена опция автоматического расчета (по мере ввода формул в документ, эти формулы сразу рассчитываются). Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.
Давайте я на этом остановлюсь, полагая, что задача знакомства читателя с Mathcad Express решена, и в следующих статьях блога, когда речь пойдет, собственно, о математике, я смогу использовать расчеты в Mathcad, не углубляясь в его интерфейс.
В заключение, адресую заинтересовавшегося читателя к своему видеокурсу по математическому анализу, который в формате МООС прошел на портале ИНТУИТ в 2014 году. Все лабораторные работы выполнены в Mathcad Prime и скачать их можно здесь. Все эти материалы на сайте Nerepetitor.ru бесплатные, регистрация не требуется.
Назначение и основные возможности программного пакета MathCAD.
Назначение и основные возможности программного пакета MathCAD.
Основные возможности
Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
Решение дифференциальных уравнений, в том числе и численными методами
Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
Использование греческого алфавита как в уравнениях, так и в тексте
Выполнение вычислений в символьном режиме
Выполнение операций с векторами и матрицами
Символьное решение систем уравнений
Поиск корней многочленов и функций
Проведение статистических расчётов и работа с распределением вероятностей
Поиск собственных чисел и векторов
Вычисления с единицами измерения
Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
Из чего состоит библиотека встроенных функций.
Мощная библиотека встроенных функций позволяет решать широкий круг инженерных и математических задач:
Типы данных.
Массивы в Mathcad
Действия с матрицами.
Построение графика функции.
16. Решение уравнения с одним неизвестным: root(f(х),х); root(f(х),х,а,b).
Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.
· f(x) — скалярная функция, определяющая уравнение f(x)=0;
· х — имя скалярной переменной, относительно которой решается уравнение;
· а, b — границы интервала, внутри которого происходит поиск корня.
Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.
Листинг 5.13. Два варианта уравнения методом секущих 
В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были «хорошими», т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.
Листинг 5.14. Пример уравнения, которое удается решить только методом секущих 
Рис. 5.5. Модельная функция f (х) (продолжение листинга 5.14)
Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки «This variable or function is not defined above», в данном случае говорящей о том, что другая переменная ранее не определена.
ПРИМЕЧАНИЕ
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.
Листинг 5.15. Поиск корней уравнения, зависящего от двух переменных 
Наложение связей.
Наложение связей в опорных узлах
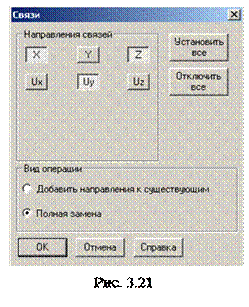
Для выполнения этой операции во вкладке Назначение инструментальной панели с помощью кнопки Установка связей в узлах 
вызываем диалоговое окно Связи. В режиме Полная замена активизируем кнопки X, Z, UY(рис. 3.21) и нажимаем кнопку OK. Выделяем курсором на схеме узлы: 1, 2 и нажимаем кнопку Подтверждение 
инструментальной панели, которая обеспечивает жесткое защемление опорных узлов 1 и 2 рамы в плоскости XоZ. Подобную операцию повторяем для шарнирно-неподвижного узла 3 (активизацией кнопок X, Z). Визуальный контроль правильности постановки опорных связей выполняем нажатием кнопки Связи 
на панели Фильтры отображения.
Задание нагрузок.
Функции задания нагрузок содержатся в разделе Загружения инструментальной панели.
Режим задания нагрузок включает функции, обеспечивающие автоматическое формирование собственного веса конструкции, задание динамических и статических нагрузок различного вида на узлы и элементы схемы, сохранение назначенных нагрузок в виде схем загружений или групп нагрузок. Зададим нагрузки на учебную расчетную схему в виде двух загружений:
Загружение 1 – описывает постоянную нагрузку на перекрытиях и покрытиях и собственный вес колонн, которые задаются как равномерно распределенная нагрузка на ригели – 4.36 т/м, и равномерно распределенная нагрузка на колонны – 0.66 т/м. Нагрузки задаются по направлению оси Z общей системы координат;
Для задания этих нагрузок воспользуемся следующими кнопками инструментальной панели:
Для ввода нагрузок необходимо выполнить следующие операции:
Для записи загружения надо нажать кнопку в инструментальной панели. В диалоговом окне Сохранить загружение ввести имя загружения и нажать кнопку ОК. Ввод имени не является обязательным, но эта информация позволяет лучше ориентироваться при анализе исходных данных и результатов расчета. Номер загружению будет присваивается автоматически (с согласия пользователя), о чем сообщается в специальном окне.
Перед тем, как ввести следующее загружение, воспользуйтесь операцией – очистка текущего загружения. При ее выполнении происходит очистка схемы от нагрузок текущего загружения. После этого можно готовить новое загружение. Если при записи загружения ему присвоить номер ранее созданного, то оно будет записано вместо него.
Раздел Деформации.
В этом режиме предусмотрено выполнение следующих функций отображения результатов:
– вывод деформированной схемы на фоне исходной;
– вывод деформированной схемы;
– вывод значений перемещений по заданному направлению в узлах расчетной схемы;
– цветовое отображение значений перемещений по заданному направлению в узлах расчетной схемы;
– отображение исходного состояния схемы;
– отображение на проекциях деформированной схемы на фоне исходной;
– вывод изополей перемещений для пластинчатых элементов;
– вывод изополей и изолиний перемещений для пластинчатых элементов;
– вывод изолиний перемещений для пластинчатых элементов;
– установка параметров цветовой шкалы;
– отображение приведенных узловых масс;
– формирование видеоклипов перемещений для статических и динамических загружений;
– анимация перемещений для статических и
После линейного расчета открываем в дереве проекта раздел Результаты, а в нем подраздел «Графический анализ». В открывшемся окне открываем инструментальную панель Деформации и нажимаем кнопку «Совместное отображение исходной и деформированной схемы». Рядом с исходной схемой появится картина деформированной схемы (без указания численных значений перемещений узлов).
Кнопки Параметры вывода.
Для назначения правил формирования и оформления результатов используется кнопка Параметры вывода, после нажатия которой появляется диалоговое окно Состав выходных таблиц.
Из этого окна осуществляется доступ к следующим функциям назначения параметров:
• список узлов или элементов, для которых выводятся результаты;
• параметры настройки генератора таблиц;
• выходные единицы измерения. Параметры настройки задаются в диалоговых окнах, вызов которых выполняется нажатием соответствующих кнопок.
В окне Параметры вывода, которое вызывается после нажатия одноименной кнопки, можно назначить количество строк на странице и ширину таблиц, точность вывода перемещений и усилий, выбрать тип таблицы, определить формат выходного файла, ориентацию страниц, размер шрифта и др.
Используя соответствующую маску вывода, можно настроить программу на печать только определенных видов силовых факторов или перемещений.
Назначение и основные возможности программного пакета MathCAD.
Основные возможности
Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
Решение дифференциальных уравнений, в том числе и численными методами
Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
Использование греческого алфавита как в уравнениях, так и в тексте
Выполнение вычислений в символьном режиме
Выполнение операций с векторами и матрицами
Символьное решение систем уравнений
Поиск корней многочленов и функций
Проведение статистических расчётов и работа с распределением вероятностей
Поиск собственных чисел и векторов
Вычисления с единицами измерения
Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.