Что такое группа алгебра

Группа (алгебра)

Гру́ппа — в абстрактной алгебре непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Ветвь математики, занимающаяся группами, называется теорией групп.

Всем знакомые вещественные числа наделены сложением — операцией, обладающей некоторым набором свойств. Похожими свойствами обладают и многие другие из объектов, которые изучает математика, — например, множество вращений плоскости вокруг начала координат. Теория групп занимается изучением взаимосвязей между этими свойствами в общем виде. Структура группы включается в различные другие алгебраические структуры, такие как поля, векторные пространства или группы Ли. Кроме того, группы являются важными инструментами в изучении симметрии во всех её проявлениях.

Содержание

Определения

Комментарии

Связанные определения

Примеры

Стандартные обозначения

Мультипликативная запись

Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:

Аддитивная запись

В коммутативной группе определяющяя операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:

Простейшие свойства

Получение новых групп из уже известных

Обобщения

См. также

Популярная литература

Научная литература

Ссылки

Полезное

Смотреть что такое «Группа (алгебра)» в других словарях:

Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия

ГРУППА — множество, на к ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло… … Физическая энциклопедия

Группа Ли — Группа (математика) Теория групп … Википедия

Группа Шрёдингера — Группа Шрёдингера это группа симметрии свободного уравнения Шрёдингера. Содержание 1 Алгебра Шрёдингера 2 Роль группы Шрёдингера в математической физике … Википедия

Группа Гейзенберга — группа, состоящая из квадратных матриц вида где элементы a, b, c принадлежат какому либо коммутативному кольцу с единицей. В качестве такого кольца R чаще всего берется: кольцо вещественных чисел так называемая непрерывная группа Гейзенберга,… … Википедия

Алгебра Темперли — Алгебра Темперли Либа, в статистической механике алгебра, при помощи которой строятся некоторые трансфер матрицы. Открыты Невиллом Темперли и Эллиотом Либом. Также алгебра применяется в теории интегрируемых моделей, имеет отношение… … Википедия

АЛГЕБРА МЕР — алгебра М(G).комплексных регулярных борелевских мер на локально компактной абелевой группе G, имеющих ограниченную вариацию, с обычными линейными операциями и сверткой в качестве умножения (см. Гармонический анализ абстрактный). Свертка полностью … Математическая энциклопедия

АЛГЕБРА С ДЕЛЕНИЕМ — алгебра Анад полем F, для любых элементов и bк рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные… … Математическая энциклопедия

ГРУППА СУСЛОВИЕМ КОНЕЧНОСТИ — группа, элементы или подгруппы к рой удовлетворяют тому или иному условию конечности. Под условием конечности в теории групп понимается любое такое свойство, присущее всем конечным группам, что существуют бесконечные группы, к рые им не обладают … Математическая энциклопедия

Источник

Группы, кольца, поля в математике

Группа: определение и примеры групп

Множество с алгебраической операцией называется группой, если выполняются следующие условия:

1) операция в ассоциативна: ;

2) в существует нейтральный элемент ;

Решение. Действительно, операция умножения определена на указанном множестве, так как

Кольцо

1) относительно операции сложения множество — коммутативная группа, т.е.

а) операция сложения коммутативна: ;

б) операция сложения ассоциативна: ;

в) существует нулевой элемент ;

г) для каждого элемента существует противоположный ему элемент ;

2) операция умножения в множестве ассоциативна:

3) операции сложения и умножения связаны законами дистрибутивности:

Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.

Если операция коммутативна, то дистрибутивность слева операции относительно операции влечет дистрибутивность справа, так как

Решение. В самом деле, для любых положительных действительных чисел справедливы равенства

Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность слева относительно умножения опровергается примером

Пример В.7. Доказать, что множество чисел вида, где и — целые числа, является кольцом:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:

Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.

Поле: определение и примеры полей

1) — коммутативное кольцо с единицей ;

Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.

Пример В.8. На множестве трех целых чисел определим две операции:

1) «сложение по модулю 3» — остаток от деления суммы на 3 (обозначим через );

2) «умножение по модулю 3» — остаток от деления произведения на 3 (обозначим через ).

Доказать, что множество является полем относительно введенных операций.

– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:

– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:

Рассматриваемые в примере операции «сложения по модулю 3» и «умножения по модулю 3» можно представить в виде

Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция «сложения по модулю 3» коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства следует, что

Коммутативность доказана. Заметим, впрочем, что коммутативность «сложения по модулю 3» видна непосредственно по таблице (см. рис.В.2): слагаемые и в таблице можно поменять местами, при этом таблица не изменится.

Из равенства следует, что

Ассоциативность «сложения по модулю 3» доказана.

Итак, множество относительно операции «сложения по модулю 3» является коммутативной группой.

Операция «умножение по модулю 3» ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:

Следовательно, операция «умножения по модулю 3» дистрибутивна слева относительно операции «сложения по модулю 3». Дистрибутивность справа можно не проверять, так как обе операции коммутативны.

Единичным элементом служит число 1 (что видно по таблице «умножения по модулю 3»). Следовательно, — коммутативное кольцо с единицей.

Пример В.9. Доказать, что множество чисел вида, где и — рациональные числа, является полем:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:

Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.

Источник

Группа (математика)

Существуют математические объекты не являющиеся числами, но над ними мы имеем возможность совершать алгебраические действия. Свойства этих действий напоминают свойства действий над числами. Это делает необходимой сформулировать более общие понятия.

Определение 1. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов этого множества третий элемент − результат действия. Предполагается, что действие ассоциативно, т.е.

где ○− знак действия.

Если операция коммутативна, т.е.

Рассмотрим примеры групп:

1. Множество всех целых чисел относительно сложения.

Действительно, операция сложения ассоциативна (a+b)+c=a+(b+c). Нейтральным элементом является 0 (a+0=0+a=a). Наконец, обратным для элемента а является −a ( a+(−a)=(−a)+a=0).

2. Множество положительных рациональных чисел относительно умножения.

Покажем, что это множество удовлетворяет всем трем пунктам определения 2. Ассоциативность очевидна ( (ab)c=a(bc) ). Нейтральным элементом является 1 ( a·1=1·a=a ).И, наконец, обратным элементом для a является ().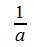

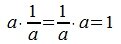
3. Множество квадратных матриц относительно сложения.

Ассоциативность сложения очевидно следует из правил сложения матриц (a+b)+c=a+(b+c). Нейтральным элементом является нулевая матрица, а обратным (противоположным) элементом является нулевая матрица.

Все вышеизложенные примеры групп являются также коммутативными. Приведем пример некоммутативной группы.

4. Множество квадратных невырожденных матриц относительно умножения.

Действительно. Ассоциативность умножения матриц сохраняется. Нейтральным элементом является единичная матрица. Единичная матрица является невырожденной, умножение невырожденных матриц будет невырожденным, следовательно всегда существует обратная матрица. При множестве матриц порядка n≥2 мы имеем дело с некоммутативной группой т.к. умножение матриц в общем случае некоммутативна ab≠ba.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Некоторые алгебраические структуры

Существует два подхода к изложению основ теории групп в учебном курсе высшей алгебры. Первый — чисто формальный, «сверху-вниз»: этот объект, его обобщения и обеспечивающая их терминология излагаются в начале курса, а впоследствии на формально введенном языке формулируются результаты из конкретных разделов алгебры. Я придерживаюсь противоположного подхода: теория групп — это «надстройка над несколькими блоками фундамента», и построение курса алгебры надо начинать именно с закладки отдельных блоков — изложением конкретных разделов (целые числа, полиномы, матрицы). И только потом устанавливать связи между ними, «перебрасывать мостики» и «навешивать узоры». Не собираясь обосновывать здесь правильность выбранной методологии (см. ☞ Правила пользования настоящим ресурсом ), я сейчас просто проясняю причину по которой, например, в разделе ПОЛИНОМ говорится о «полиноме над множеством», а не о «полиноме над полем».

А в завершение этого комментария привожу ☞ ЦИТАТУ.

Бинарная операция

Пример. Приведем несколько случаев некоммутативности:

Определение группы

Пример. На множестве четных чисел не существует нейтрального элемента относительно умножения.

Примеры групп

Аддитивная группа целых чисел

Является ли это множество полугруппой?

Классы вычетов

Корни из единицы

Образует ли множество матриц

Монотонные функции

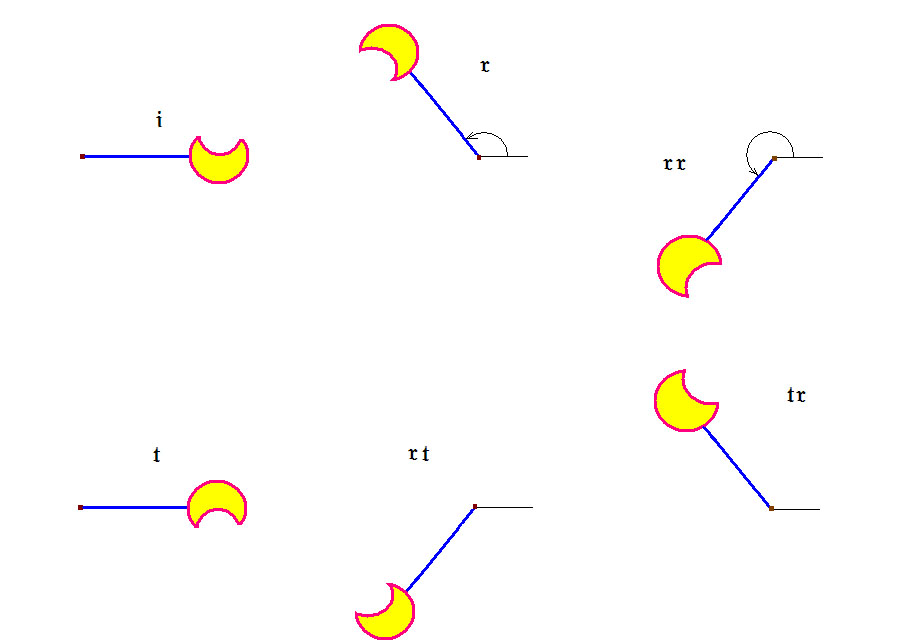
Отображения плоских фигур

Перестановки

Образующие элементы группы

Простейший случай — это группа с одной образующей.

Доказать, что циклическая группа всегда абелева.

Разумеется, подгруппа может порождаться и не одним образующим.

Доказательство ☞ ЗДЕСЬ.

Порядок любого элемента конечной группы является делителем порядка группы.

Образует ли группу относительно умножения множество матриц

Факторгруппа

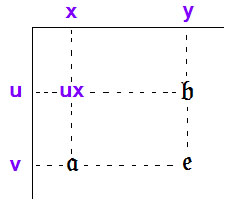
Таблица умножения

Какая информация необходима для полного задания группы как математического объекта?

Для абелевой группы таблица умножения будет симметричной относительно главной диагонали, т.е. диагонали, идущей из левого верхнего в правый нижний угол таблицы.

Перечислим теперь некоторые свойства таблицы умножения.

Остальные свойства будем нумеровать

2. Каждая строка таблицы образована какой-то перестановкой элементов нулевой строки (и аналогичное утверждение справедливо относительно столбцов).

Для второго множества из теоремы доказательство аналогично. ♦

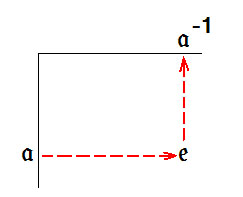
4. Аксиома об обратном элементе переформулируется следующим образом: если в таблице сложилась конфигурация

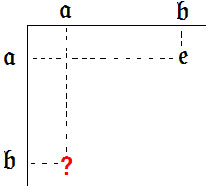
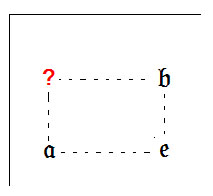
5. Рассмотрим следующую конфигурацию, сложившуюся в таблице умножения:

Доказательство. Пусть конфигурация соответствует следующему расположению элементов группы в нулевых строке и столбце:

Изоморфизм групп

Может ли группа быть изоморфна собственной подгруппе?

Доказать, что любые две циклические группы одинакового порядка (конечного или бесконечного) изоморфны.

Кольцо

В предыдущих пунктах мы анализировали множества с точки зрения одной определенной бинарной операции. Однако, часть рассмотренных примеров составляли множества, в которых были определены и другие операции.

Идеал

В этом обозначении случилась коллизия с обозначением циклической группы; однако альтернативные варианты, принятые в литературе, приводят к другим коллизиям.

В отличие от линейных пространств, на базисные элементы не накладывается ограничений типа линейной независимости.

Поле из полиномов

Алгебра

Источник

Алгебра

А́лгебра (от араб. الجبر ‎‎, «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.

Алгебраическая система — упорядоченная пара множеств . Первое множество () — элементы какой либо природы (числа, понятия, буквы). Второе множество () — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.

Содержание

История

Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.

За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]

В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.

Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.

Классификация

Алгебру можно грубо разделить на следующие категории:

В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:

Элементарная алгебра

Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:

Источник