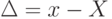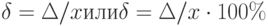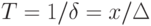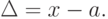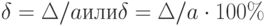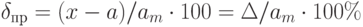Что такое грубые систематические и случайные погрешности измерений
Что такое грубые, случайные и систематические погрешности



Гурбыми называются ошибки превосходящие по абсолютной величине некоторые устновленные для данных условий измерений, предел они происходят в большинстве случаев в результате промахов и просчетов исполнителя. Такие ошибки обнаруживают повторными измерениями а результаты содержащие их бракуют и заменяют новыми.
Случайные ошибки это ошибки размер и влияние которых на каждый отдельный результат измерения остается неизвестным. Величину и знак случайно ошибки заранее установить нельзя. Однако теоретические исследования и многолетний опыт измерений показывают, что случайные ошибки подчинены определенным вероятностным закономерностям, изучение которых дает возможность получить наиболее надежный результат. Свойства случайных ошибок: 1 при определенных условиях измерения случайные ошибки по абсолютной величине не могут превышать известного предела называемого предельной ошибкой. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые ошибки. 2. Положительные и отрицательные случайные ошибки примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических ошибок. 3 Чем больше абсолютная величина ошибок тем реже она встречается в ряже измерений. 4 Среднее арифметическое из случайных ошибок измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании числа измерение стремится к 0.
Систематическими называют ошибки которые по знаку или величина однообразно повторяются многократных измерений.
Равноточные и неравноточные измерения.
Неравноточными называют такие измерения которые выполнены соответственно с разными квадратическими ошибками за счет разного количества приемов, использования приборов различной точности, разных условии и тп.
Погрешности измерений и их классификация
Все измерения сопровождаются погрешностями. Различают грубые, систематические и случайные погрешности.
Грубые погрешности измерений, к которым относятся просчеты, при повторных измерениях обнаруживаются и их из результатов измерений исключают.
Систематические погрешности измерений действуют на результаты измерения по определенному закону, изменяя результат на одну и ту же величину. Для того чтобы выявить, а затем исключить или учесть систематическую погрешность необходимо сделать исследование и юстировку инструментов.
Случайные погрешности измерений неизбежны в процессе измерений и не могут быть исключены из результатов измерений.
Изучение свойств этих ошибок позволяет разработать методы для оценки точности результатов измерений и определить вероятнейшие значения измеренных величин. Решением этих вопросов занимается теория ошибок геодезических измерений, в основу которой положены основные свойства случайных ошибок.
Свойства случайных погрешностей
1. Для данных условий измерений погрешности не могут превышать по абсолютной величине известного предела.
2. Малые по абсолютной величине погрешности встречаются чаще, чем большие.
3. Одинаковые по абсолютной величине и разные по знакам погрешности возможны одинаково.
4. Среднее арифметическое из случайных погрешностей измерений величины стремиться к нулю при неограниченном числе измерений.
Принцип арифметической средины.
Среднее арифметическое или арифметическая средина равноточных измерений одной и той же величины стремится к истинному значению при неограниченном возрастании числа измерений.
Пусть l1; l2; … ln – результаты равноточных измерений, истинное значение которых Х. Тогда истинные погрешности получаем как разности:
На основании четвертого свойства случайных погрешностей при увеличении числа измерений [?]/n стремиться к нулю. Таким образом, среднее арифметическое Х0= [l]/n стремиться к истинному значению измеряемой величины Х.
Средняя квадратическая погрешность. Предельная и относительная погрешность.
Средняя квадратическая погрешность арифметической средины.
Арифметическая средина является наиболее надежным результатом из многократных измерений. Ее точность характеризуется ошибкой, величина которой должна быть меньше заданной величины, чем количество измерений. Средняя квадратическая погрешность арифметической средины определяется по формуле:
Оценка точности по вероятнейшей погрешности.
В большинстве случаев истинное значение измеряемой величины не известно, поэтому для вычисления средней квадратической ошибки используют отклонения результатов измерений от их среднего арифметического. Эти отклонения называют вероятнейшими погрешностями. Для вычисления средней квадратической погрешности по вероятнейшим вычисляют разности между каждым результатом измерения и арифметической срединой Х0, эти разности возводят в квадрат и получают среднюю квадратическую погрешность по формуле Бесселя:
[l] – nХ0 = [V], Суммарное уравнение,
Среднюю квадратическую погрешность арифметической средины по вероятнейшим ошибкам определяют по формуле:
Среднюю квадратичную ошибку результата по разностям двойных измерений вычисляют по формуле:
Измерения могут быть равноточные и неравноточные. Неравноточные измерения-это измерения одной и той же величины, которые выполняют разными приборами или исполнителями. По разным технологиям или в различных условиях. Неравноточные измерения имеют разный вес, тогда как равноточные измерения имеют одинаковый вес, т.е.степень доверия к результату. Весом Р называют отношение целого числа С к квадрату средней квадратической погрешности Р = С/m2.
Из полученных неравноточных измерений, зная их вес, получают общую арифметическую средину или весовое среднее L0 по формуле:
Пример 1. Линия измерена два раза и получили первый раз среднее арифметическое l1 = 212,45 с весом Р = 2.
Вторично эту же линию измеряли четыре раза и нашли среднее арифметическое l2 = 212,38 с весом Р = 4, тогда
Погрешности измерений и их классификация – статья на сайте “студент-строитель.ру”
Посмотрите также:
Нивелирование поверхности Производится с целью получения более точного плана с изображением рельефа местности в равнинных районах.
Тахеометрическая съемка В основе лежит метод пространственного определения точек местности одним наведением зрительной трубы на рейку, установленную на точке (рис.
Геодезические сети Геодезические сети представляют собой совокупность точек местности, положения которых заслеплено и определено на земной поверхности с высокой точностью.
Систематические, случайные, грубые, промахи
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
ПОНЯТИЕ ИЗМЕРЕНИЯ, ПОГРЕШНОСТИ И ТОЧНОСТИ
ОСНОВЫ МЕТРОЛОГИИ
Лекция 6.
Чтобы иметь представление о физической величине с количественной точки зрения, необходимо выразить её числом, т.е. измерить.
Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величины.
По способу получения числового значения искомой величины (иначе, по характеру уравнения измерения) измерения делят на прямые, косвенные, совокупные и совместные. Такая классификация важна с точки зрения обработки экспериментальных данных и расчета погрешностей.
При прямом измерении искомое значение измеряемой величины находят непосредственно их опытных данных, то есть прямо по шкале прибора (иногда показания прибора умножают на некоторый коэффициент, вводят соответствующие поправки и так далее).
При этом простота и сложность процесса измерений во внимание не принимаются. Существенным признаком прямых измерений является то, что результат выражается в тех же единицах, что и измеряемая величина.
При косвенных измерениях искомое значение измеряемой величины находят на основании известной зависимости между этой величиной и величинами, которые находят в результате прямых, а иногда и косвенных, совместных или совокупных измерений.
Например, нахождение плотности твердого тела как отношения массы тела к его объему, причем, масса и объем измеряются непосредственно нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения: измерение расхода жидкости по перепаду давления в сужающем устройстве.
Таким образом, косвенное измерение всегда связано с расчетом (однако измерение поправки не превращает прямое измерение в косвенное).
Прибегать к косвенным измерениям приходится тогда, когда искомую величину невозможно или сложно измерить непосредственно путем прямого измерения.
Погрешности классифицируются по ряду признаков.
По способу выражения погрешности разделяются на абсолютные, относительные и приведенные.
Точность измерений по ДСТУ 2681-94 определяется как качество измерений, отражающее близость полученного измеренного значения к истинному значению измеряемой величины. Количественно точность характеризуется числом, равным обратному значению относительной погрешности, выраженной в долях измеряемой величины:
При γ = 0,001 точность измерений равна 1000. В метрологии и при практических измерениях точность, как правило, количественно не оценивается, а характеризуется косвенно, с помощью погрешности измерения.
Иногда диапазон измерений прибора охватывает и нулевое значение. Поскольку значение относительной погрешности зависит от текущего значения Х, то при Х = 0 относительная погрешность стремится к бесконечности. Поэтому в измерительной технике было введено понятие приведенной погрешности.Она равна отношению абсолютной погрешности к некоторому нормированному значению Хн.



где Хн может быть диапазон измерения, длина шкалы или др.
По характеру изменения погрешности могут быть:
Примером второго типа систематических погрешностей является большинство дополнительных погрешностей, являющихся величин (температура, напряжение и т.п.)
Основное свойство систематических погрешностей состоит в том, что они могут быть почти полностью устранены введением соответствующих поправок.
Для изучения систематических погрешностей очень важно знать причины их возникновения и закономерности их проявления.
В зависимости от причин возникновения систематические погрешности делятся на несколько групп:
1. Инструментальные погрешности, зависящие от самих измерительных средств, и вызваны их несовершенством.
2. Погрешности, возникающие в результате неправильной установки прибора.
3. Погрешности, вызываемые условиями эксплуатации: отклонение температуры от нормальной, влиянием магнитных и электрических полей, повышенным или пониженным атмосферным давлением и др.
4. Методические погрешности, возникающие из-за несовершенства метода измерения, применение неточных эмпирических формул и зависимостей.
5. Субъективные (личные) погрешности, зависящие от индивидуальных свойств наблюдателя (разные наблюдатели могут по-разному отсчитывать показания стрелочных приборов).
Особенностью систематических погрешностей является то, что их присутствие чрезвычайно трудно обнаружить, так как внешне они себя никак не проявляют и поэтому долгое время могут оставаться незамеченными. Единственный способ их обнаружения состоит в проверке нуля прибора и проверки чувствительности путем повторной аттестации прибора по образцовым приборам.
Случайными называются погрешности, неопределенные по своей величине или не достаточно изученные, в появлении значений которых не удалось установить какой-либо закономерности. Они определяются сложной совокупностью причин, которые трудно поддаются анализу. Случайные погрешности легко обнаруживаются при повторных измерениях в виде некоторого разброса результатов. Для совокупности случайных погрешностей можно указать вероятность появления их различных значений.
В подавляющем большинстве случаев процесс появления случайных погрешностей есть стационарный случайный процесс. Поэтому случайные погрешности характеризуются законом распределения их вероятностей или указанием параметров этого закона. Поскольку большинство составляющих погрешности реальных приборов появляются именно как случайные, то их вероятностное описание является основным научным методом теории погрешностей.
Грубые погрешности существенно превышают погрешности, оправданные условиями измерения, свойствами примененных средств измерений, методом измерений и квалификацией экспериментатора. Такие погрешности могут возникнуть, например, при резком изменении в сети питания (если оно, в принципе, оказывает влияние на результат измерения). Грубые погрешности обнаруживаются статистическими методами и обычно исключаются из рассмотрения.
Причинами возникновения инструментальных погрешностей могут быть: низкое качество изготовления узлов прибора (инструмента), например, трение в опорах подвижной системы, зазоры в сочленениях деталей, неточность изготовления, сборки и регулировки деталей механизмов, а также изменение с температурой модуля упругости материалов чувствительных элементов, электрических и монтажных сопротивлений, линейных размеров деталей приборов (так называемые инструментальные погрешности).
Однако есть погрешности, которые останутся даже в том случае, если элементы прибора будут идеальными. Так, например, выходной сигнал мостовой неуравновешенной схемы зависит от изменения напряжения питания. Если вместо неуравновешенной системы применить уравновешенную с нулевым отсчетом, то есть заменить один метод измерения другим, тогда указанной методической погрешности не будет.
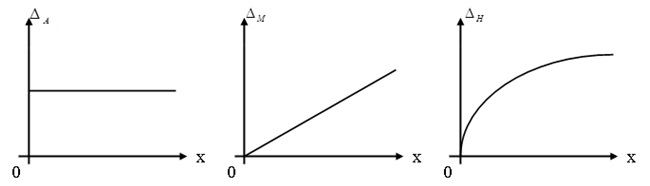
При анализе погрешностей большое значение имеет разделение погрешностей по их зависимости от значений Х измеряемой величины. Если абсолютная погрешность измерения дельта-ноль при всех значениях измеряемой величины Х постоянна, то такая погрешность называется аддитивной (в переводе с латинского «получаемая путем сложения») или погрешность нуля. Если она является систематической, то есть имеет один и тот же знак (положительная или отрицательная), то она может быть скорректирована путем нулевого положения указателя.
Если абсолютная погрешность измерения пропорциональна текущему значению измеряемой величины Х (может быть систематической и случайной), то такая погрешность называется мультипликативной погрешностью чувствительности.
Причинами таких погрешностей могут быть: изменение коэффициента усиления усилителя, коэффициента деления делителя и другие.
Погрешности, не зависящие от скорости, называются статическими. Погрешности, возникающие при возрастании скорости, называются динамическими. Последние здесь не рассматриваются.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Элементы теории погрешностей
Понятие погрешности
При любой степени совершенства и точности измерительной аппаратуры, рационально спланированной методике измерений, тщательности выполнения измерительных операций результат измерений отличается от истинного значения физической величины.
Иначе говоря, при всяком измерении неизбежны обусловленные разнообразными причинами отклонения результата измерения ( x ) от истинного значения измеряемой величины (X). Эти отклонения называют погрешностями измерений.
Это соотношение служит исходным для теоретического анализа погрешностей. На практике же из-за невозможности определить истинное значение вместо него берут действительное значение измеряемой величины, например, среднеарифметическое результатов наблюдений при измерениях с многократными наблюдениями.
Истинным называется значение ФВ (физической величины), идеальным образом характеризующее свойство данного объекта, как в количественном, так и качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить её в виде числовых значений.
Действительным называется значение ФВ, найденное экспериментально и настолько близкое к истинному, что в поставленной измерительной задаче оно может быть использовано вместо него.
Погрешность измерений иногда удобно характеризовать ее относительным значением:
Следует также различать погрешность результата измерения и погрешность средства измерений ( СИ ). Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам.
Величину, обратную относительной погрешности, называют точностью:
Правильное количественное представление о качестве измерений получают путем указания погрешности или точности. Соответствующие формулировки будут:
Точность 1000 соответствует относительной погрешности 0,1%, точность 25 – относительной погрешности 4%.
Классификация погрешностей
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом ( по знаку и значению) в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях.
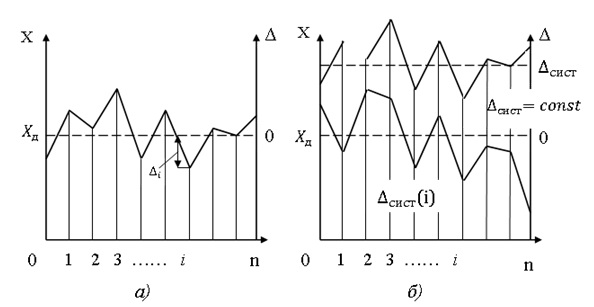
В появлении таких погрешностей, изображенных на рис. 2.1(а), не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их можно существенно уменьшить, увеличив число наблюдений.
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. Постоянная и переменная систематические погрешности показаны на рис. 2.1(б). Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.
Прогрессирующая погрешность – это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не может быть сведено к понятиям случайной и систематической погрешностей.
По способу выражения разделяют абсолютные, относительные и приведенные погрешности.
Алгебраическую разность измеряемого значения величины x и действительного ее значения a называют абсолютной погрешностью измерения 
Отношение абсолютной погрешности к действительному значению измеряемой величины 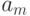
Отношение абсолютной погрешности к максимальному возможному значению измеряемой величины (например, к верхнему пределу измерений прибора или к диапазону измерений) называется приведенной погрешностью 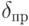
В зависимости от причин возникновения различают инструментальные погрешности измерения, погрешности метода измерений, погрешности из-за изменения условий измерения и субъективные погрешности измерения.
Погрешность метода измерений – составляющая систематической погрешности измерений из-за несовершенства принятого метода измерений, эта погрешность обусловлена:
Погрешность (измерения) из-за изменения условий измерения – это составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности: аддитивные 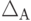
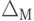
Погрешности измерений
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
Классификация погрешностей
По форме представления
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
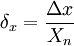
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
По причине возникновения
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.