Что такое грубые погрешности

17.04.202227.04.2022 admin 0 Comments

Грубые погрешности.

Грубая погрешность, или промах, – это погрешность результатаотдельного измерения, входящего в ряд измерений, которая для данныхусловий резко отличается от остальных результатов этого ряда.Источником грубых погрешностей нередко бывают ошибки, допущенныеоператором во время измерений. К ним можно отнести:

− неправильный отсчет по шкале измерительного прибора,происходящий из-за неверного учета цены малых делений шкалы;

− неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь.

Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путем повторных измерений. Их причинами могут быть внезапные и кратковременные изменения условий измерения или оставшиеся незамеченными неисправности в аппаратуре. Под промахом понимается значение погрешности, отклонение которого от центра распределения существенно превышает значение, оправданное объективными условиями измерения. Поэтому с точки зрения теории вероятности появление промаха маловероятно.

Особую неприятность доставляют отсчеты, которые хотя и не входят в компактную группу основной массы отсчетов выборки, но и не удалены от нее на значительное расстояние, – так называемые предполагаемые промахи. Отбрасывание «слишком» уда-

ленных от центра выборки отсчетов называется цензурированием выборки.

Это осуществляется с помощью специальных критериев. При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения

промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений.

Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез Проверяемая гипотеза состоит в утверждении, что результат наблюдения х, не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.

Для выявления грубых погрешностей задаются вероятностью q —

уровнем значимости того, что сомнительный результат действительно мог

иметь место в данной совокупности результатов измерений.

Следует заметить, что в нормативной документации по статистическому контролю качества продукции и учебниках по управлению качеством вероятность признать негодной партию годных изделий называют “риском производителя”, а вероятность принять негодную партию – “риском потребителя

Проверку статистической гипотезы проводят для принятого уровня значимости q (принимается равным 0,1; 0,05; 0,01 и т. д.). Так принятый уровень значимости q = 0,05 означает, что выдвинутая нулевая статистическая гипотеза может быть принята с доверительной вероятностью P = 0,95.. Нулевая статистическая гипотеза подтверждает принадлежность проверяемого “подозрительного” результата измерения (наблюдения) данной группе измерений.

где x_i_под – результат наблюдения, проверяемый на наличие грубой погрешности;

Таким образом, границы погрешности зависят от вида распределения, объема выборки и выбранной доверительной вероятности.

Критерий «трех сигм» применяется для результатов измерений,

распределенных по нормальному закону. По этому критерию считается,

что результат, возникающий с вероятностью q 3S_x , где S_x – оценка СКО

измерений. Величины X и S_x вычисляют без учета экстремальных

значений x_i . Данный критерий надежен при числе измерений n ≥ 20. 50.

Это правило обычно считается слишком жестким, поэтому

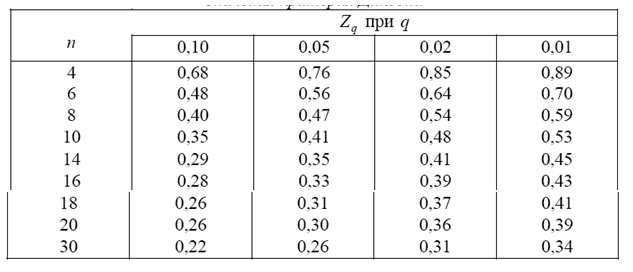
рекомендуется назначать границу цензурирования в зависимости от

приведены в таблице 4.3 [27].

Применение рассмотренных критериев требует осмотрительности и

учета объективных условий измерений. Конечно, оператор должен

исключить результат наблюдения с явной грубой погрешностью и

выполнить новое измерение. Но он не имеет права отбрасывать более или

менее резко отличающиеся от других результаты наблюдений. В

сомнительных случаях лучше сделать дополнительные измерения (не

взамен сомнительных, а кроме них) и затем привлекать на помощь

рассмотренные выше статистические критерии. Кроме рассмотренных

критериев существуют и другие, например критерии Граббса и Шовенэ

Пример 1. При измерении диаметра вала микрометром были получены

значения: 12,24; 12,26; 12,28; 12,28; 12,31; 12,34; 12,40; 12,41; 12,42; 12,42;

12,45; 12,80 мм. Число измерений n = 12. Последний результат (12,80 мм) вы-

зывает сомнения. Принимаем Р= 0,95, тогда q = 0,05.

Выполнив расчеты, получили значения − х = 12,38 мм; S = 0,15 мм. Так

как n βти результат х_i =

х_пр= 12,80 мм необходимо «отбросить», как промах.

После исключения результатов, содержащих промахи, определяют но-

вые значения хи S и, если есть сомнения, процедуру проверки наличия прома-

Источник

Грубые погрешности и методы их исключения

Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Тамбовский государственный технический университет»

ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ

Утверждено Методическим советом ТГТУ в качестве

методических указаний для студентов, обучающихся по направлениям

27.03.02 «Управление качеством», 15.03.06 «Мехатроника и робототехника»,

13.03.02 «Электроэнергетика и электротехника»,

13.03.01 «Теплоэнергетика и теплотехника»,

22.04.01 «Материаловедение и технологии материалов»

Доктор технических наук

Утверждено Методическим советом ТГТУ

ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ

Цель работы: изучить классификацию погрешностей; ознакомиться с методами исключения грубых погрешностей; получить практические навыки обработки результатов измерений по обнаружению грубых погрешностей.

Задание. Решить задачи, согласно полученному варианту (см. табл. 6).

Грубой погрешностью (промахом) называется погрешность, существенно превышающая значение ожидаемой погрешности при данных условиях проведения измерительного эксперимента. Обычно грубая погрешность является следствием значительного внезапного изменения условий эксперимента: броска тока источника электропитания; не учтенное экспериментатором изменение температуры окружающей среды (при длительном эксперименте); неправильный отсчет показаний из-за отвлечения внимания экспериментатора и др.

При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, такие как критерий Романовского, критерий Шарлье, критерий Диксона.

Для выявления грубых погрешностей задаются уровнем значимости q (вероятностью P) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.

Критерий Романовского применяется, если число измерений n 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютного значению среднее арифметическое значение на величину , будет , где — значение нормированной функции Лапласа для X = Kш.