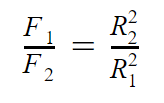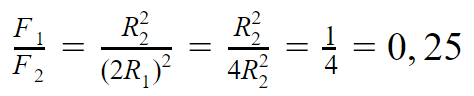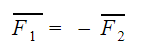Что такое гравитационное взаимодействие в естествознании

Закон всемирного тяготения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

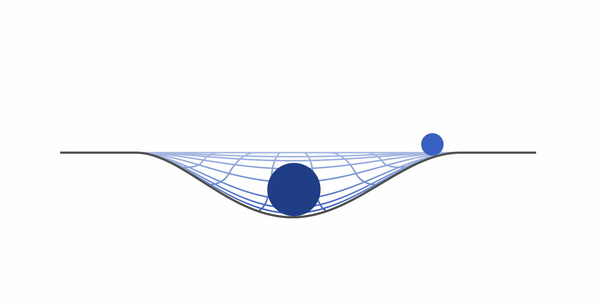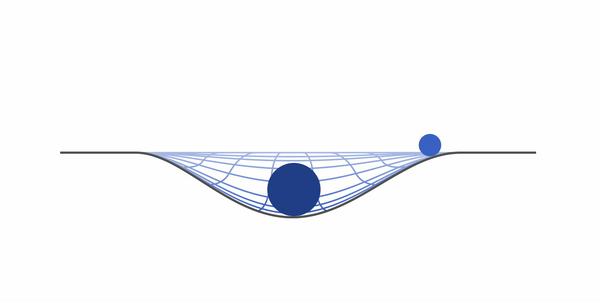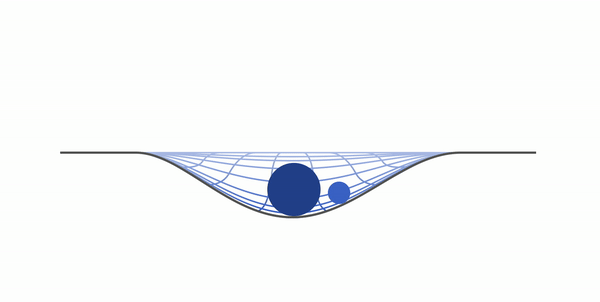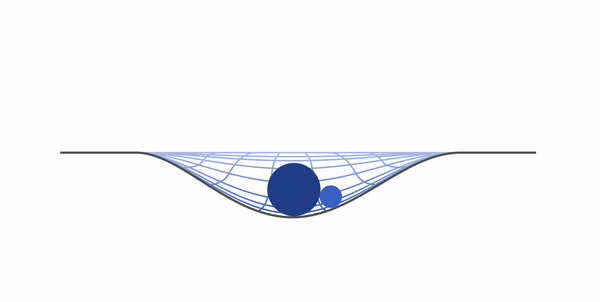
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

Закон всемирного тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁=2R₂.

Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести

F — сила тяжести [Н]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

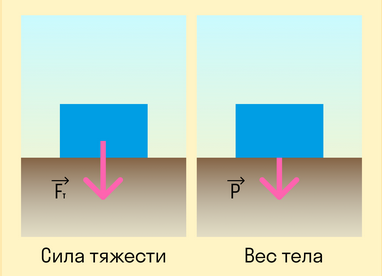
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

Приравниваем правые части:

Делим на массу левую и правую части:

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Закон всемирного тяготения

g — ускорение свободного падения [м/с 2 ]

M — масса планеты [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Но разве это не зависит еще и от массы предмета?

Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈

Третий закон Ньютона

F₁ — сила, с которой первое тело действует на второе [Н]

F₂ — сила, с которой второе тело действует на первое [Н]

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

Источник

Что такое гравитационное взаимодействие в естествознании

В свой повседневной жизни человек сталкивается с множеством сил, действующих на тела: сила ветра или потока воды; давление воздуха; мощный выброс взрывающихся химических веществ; мускульная сила человека; вес предметов; давление квантов света; притяжение и отталкивание электрических зарядов; сейсмические волны, вызывающие подчас катастрофические разрушения; вулканические извержения, приводившие к гибели цивилизаций; и т.д. Одни силы дейст­вуют непосредственно при контакте с телом, другие, например гравитация, действуют на расстоянии, через пространство. Но, как вы­яснилось в результате развития естествознания, несмотря на столь большое разнообразие, все действующие в природе силы можно свести к четырем фундаментальным взаимодействиям. Именно эти взаимодейст­вия в конечном счете отвечают за все изменения в мире, именно они являются источником всех материальных преобразований тел, про­цессов. Каждое из четырех фундаментальных взаимодействий имеет сходство с тремя остальными и в то же время свои отличия. Изучение свойств фундаментальных взаимодействий составляет главную зада­чу современной физики.

Гравитация первым из четырех фундаментальных взаимодействий стала предметом научного исследования. Созданная в XVII в. ньютоновская теория гравитации (закон всемирного тяготения) позволила впервые осознать истинную роль гравитации как силы при­роды (см. 6.3.1).

Гравитация обладает рядом особенностей, отличающих ее от дру­гих фундаментальных взаимодействий. Наиболее удивительной осо­бенностью гравитации является ее малая интенсивность. Гравитаци­онное взаимодействие в 10 39 раз меньше силы взаимодействия элект­рических зарядов *. Как может такое слабое взаимодействие оказать­ся господствующей силой во Вселенной?

Все дело во второй удивительной черте гравитации — ее универ­сальности. Ничто во Вселенной не может избежать гравитации. Каж­дая частица испытывает на себе действие гравитации и сама является источником гравитации, вызывает гравитационное притяжение. Гравитация возрастает по мере образования все больших скоплений вещества. И хотя притяжение одного атома пренебрежимо мало, но результирующая сила притяжения со стороны всех атомов может быть значительной. Это проявляется и в повседневной жизни: мы ощущаем гравитацию потому, что все атомы Земли сообща притяги­вают нас. Зато в микромире роль гравитации ничтожна. Никакие квантовые эффекты в гравитации пока не доступны наблюдению.

Кроме того, гравитация — дальнодействующая сила природы. Это означает, что, хотя интенсивность гравитационного взаимодейст­вия убывает с расстоянием, оно распространяется в пространстве и может сказываться на весьма удаленных от источника телах. В астро­номическом масштабе гравитационное взаимодействие, как прави­ло, играет главную роль. Благодаря дальнодействию гравитация не позволяет Вселенной развалиться на части: она удерживает планеты на орбитах, звезды в галактиках, галактики в скоплениях, скопления в Метагалактике.

Сила гравитации, действующая между частицами, всегда пред­ставляет собой силу притяжения: она стремится сблизить частицы. Гравитационное отталкивание еще никогда не наблюдалось *.

Пока еще нет однозначного ответа на вопрос, чем является грави­тация — неким полем, искривлением пространства-времени или тем и другим вместе. На этот счет существуют разные мнения и концеп­ции (см. 10.2.4). Поэтому нет и завершенной теории квантово-гравитационного взаимодействия (см. 10.3.5).

Источник

ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ

универсальное (присущее всем видам материи) взаимодействие, самое слабое из фундам. взаимодействий элементарных частиц (см. Тяготение); имеет характер притяжения.

Смотреть что такое «ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ» в других словарях:

ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ — один из четырёх видов (наряду со слабым, сильным и электромагнитным взаимодействиями) взаимодействия элементарных частиц, обусловленный их взаимным притяжением (см. ) и осуществляемый посредством (см. (4)). Г. в. является наиболее слабым среди др … Большая политехническая энциклопедия

ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ — универсальное (присущее всем видам материи) взаимодействие, самое слабое из фундаментальных взаимодействий элементарных частиц (см. Тяготение); имеет характер притяжения … Большой Энциклопедический словарь

ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ — элементарных частиц, наиболее слабое из всех известных фундам. вз ствий. Наблюдательные проявления Г. в. связаны с его дальнодействующим хар ром и когерентным усилением гравитац. эффектов в макроскопич. масштабах (см. ТЯГОТЕНИЕ). В макропроцессах … Физическая энциклопедия

ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ — ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ, смотри Взаимодействия фундаментальные … Современная энциклопедия

Гравитационное взаимодействие — ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ, смотри Взаимодействия фундаментальные. … Иллюстрированный энциклопедический словарь

Гравитационное взаимодействие — Гравитация (всемирное тяготение, тяготение) (от лат. gravitas «тяжесть») дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том… … Википедия

гравитационное взаимодействие — универсальное (присущее всем видам материи) взаимодействие, самое слабое из фундаментальных взаимодействий элементарных частиц (см. Тяготение); имеет характер притяжения. * * * ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ,… … Энциклопедический словарь

гравитационное взаимодействие — gravitacinė sąveika statusas T sritis Standartizacija ir metrologija apibrėžtis Viena iš pagrindinių sąveikų. Jos objektai – visos masę turinčios dalelės (sistemos). Elementariųjų dalelių vyksmuose nereikšminga, tačiau lemia didelės masės kūnų… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

гравитационное взаимодействие — gravitacinė sąveika statusas T sritis fizika atitikmenys: angl. gravitational interaction vok. Gravitationswechselwirkung, f; gravitative Wechselwirkung, f rus. гравитационное взаимодействие, n pranc. interaction gravitationnelle, f … Fizikos terminų žodynas

гравитационное взаимодействие — Универсальное фундаментальное взаимодействие между всеми физическими объектами, интенсивность которого определяется их полной энергией … Политехнический терминологический толковый словарь

Источник

Классические теории гравитации

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Содержание

Гравитационное взаимодействие

.

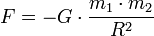
Здесь G — гравитационная постоянная, равная примерно 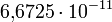м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа 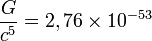(1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая [3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов. [4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. [5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО [6] :

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля. [9]

Источник