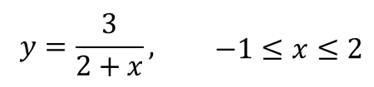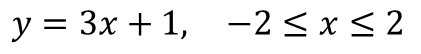Что такое график функции 7 класс

Урок алгебры в 7-м классе на тему «Линейная функция и ее график»

Разделы: Математика

Цели: рассмотреть случаи взаимного расположения прямых – графиков линейных функций; ввести понятие углового коэффициента k; развивать навыки построения прямых по координатам точек; приучать учащихся к аккуратному построению прямых.

1. Изучение нового материала.

Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где x – независимая переменная, k и b – некоторые числа.

Прямая пропорциональность является частным случаем линейной функции при b = 0.

Возьмем графики функции y = 0,5x и у = 0,5х + 2.

Если график функции у = 0,5x сдвинуть на 2 единицы вверх, то каждая точка графика функции у = 0,5х перейдет в точку графика функции у = 0,5х + 2. При этом любая точка графика у = 0,5х + 2 получается из соответствующей точки графика функции y = 0,5x.

График функции y=kx+b, где k0, есть прямая, параллельная прямой y=kx.

Если k=0, то формула y=kx+b принимает вид y = b. Графиком функции y = kx + b является прямая, параллельная оси х при b0 или сама ось х при b = 0.

Графиком линейной функции является прямая.

Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую.

Расположение графика функции y=kx+b на координатной плоскости зависит от коэффициентов k и b.

Число k называется угловым коэффициентом прямой – графика функции у = kx + b.

Если k>0, то угол наклона прямой у=kx+b к оси х острый; если k 2 – 3 нет;

б) у = 7 – 9х да; г) нет; е) да.

а) х = –1,5; у = – 3 • (– 1,5) + 1,5 = 6

х = 2,5; у = –3 • 2,5 + 1,5 = –7,5 + 1,5 = –6

х = 4; у = –3 • 4 + 1,5 = –2 + 1,5 = –10,5

Источник

График функции

Урок 14. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «График функции»

· показать на примере как строится график функции;

· ввести понятие «график функции»;

· познакомить со специальными приборами, которые вычерчивают графики функциональных зависимостей и используются в различных сферах деятельности человека.

Давайте возьмём функцию, которая задана формулой:

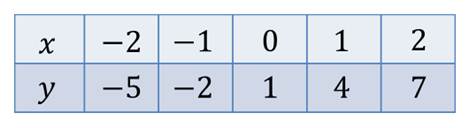
Составим таблицу значений этой функции с шагом 1.

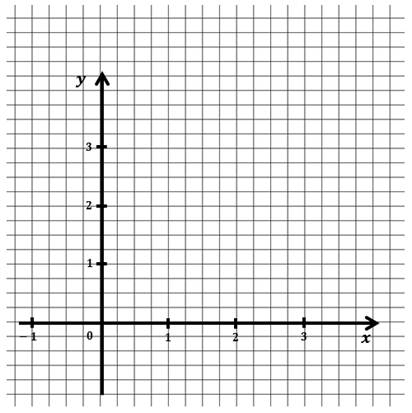
Затем изобразим систему координат. Вспомним, что горизонтально расположенную ось называют осью абсцисс. А вертикально расположенную ось – осью ординат.

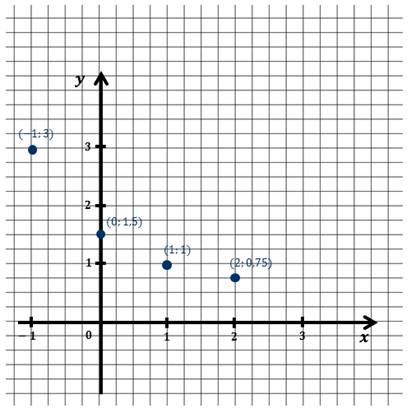
Каждую из найденных пар значений х и у изобразим точкой в координатной плоскости.

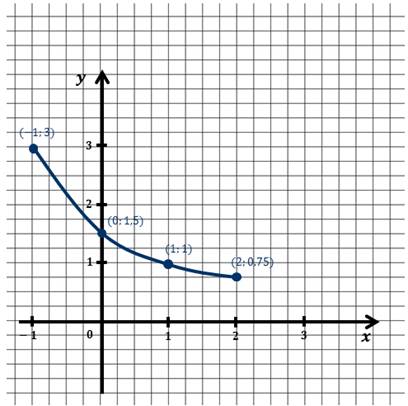
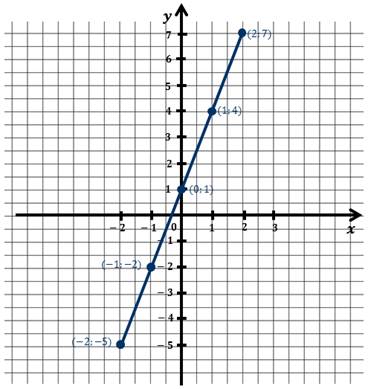
Соединим эти точки плавной линией и получим график нашей функции:

Следует отметить, что чем больше точек, принадлежащих графику мы отметим на координатной плоскости, тем более точно будет построен график функции.

Таким образом, сформулируем определение.

Графиком функции называется множество всех точек плоскости, абсциссы которых принадлежат области определения, а ординаты равны соответствующим значениям функции.

Давайте построим график ещё одной функции, заданной формулой:

Составим таблицу значений данной функции с шагом 1.

Изображаем систему координат. И отмечаем в координатной плоскости все точки, координаты которых записаны в нашей таблице.

Соединяем отмеченные точки линией. И получаем график заданной функции для заданных значений аргумента.

График функции является наглядным представлением зависимости между величинами.

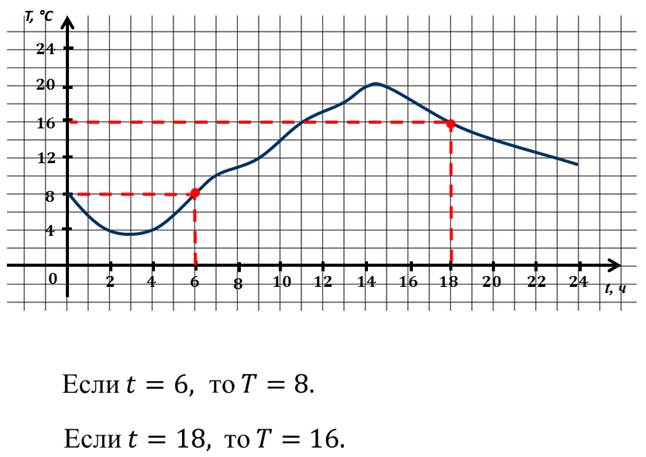
Например, на следующем графике показано, как изменяется температура воздуха в течение суток.

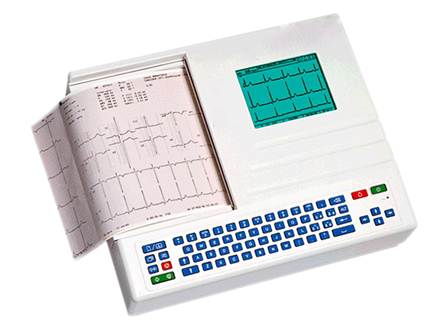
Для получения такой информации на практике используют специальный прибор, который называется термографом.

Перо вычерчивает на ленте, которая намотана на барабан, непрерывную линию, выражающую зависимость между временем и температурой воздуха.

Существуют и другие приборы, которые вычерчивают графики функциональных зависимостей.

Одним из таких является кардиограф.

Он позволяет получить графическое описание работы сердца.

А ещё есть такой прибор, как сейсмограф.

Он используется для обнаружения и регистрации колебаний почвы, которые, например, могут быть вызваны землетрясением

Источник

График функции.

Данный материал содержит определение графика функции, алгоритм построения графиков функций, примеры. Кроме того, здесь можно найти графический способ задания функции и табличный способ, определены их недостатки и преимущества. Практическая часть содержит большое количество разнообразных заданий с разным уровнем сложности.

Просмотр содержимого документа
«График функции.»

Для того, чтобы ввести понятие графического задания функции, определим сначала, что есть график функции.

Графиком функции называется множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. (Напомним, что абсцисса – это координата х, ордината – координата у).

Поскольку, по определению функции, каждому значению аргумента соответствует только одно значение функции, то для графика соблюдается такое же правило: каждой абсциссе графика соответствует только одно значение ординаты.

Например,

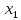
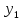
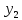
На графиках показано, что абсциссе соответствует только одно значение ; абсциссе – только одно значение . И так далее.

Итак, теперь рассмотрим графический способ задания функции.

Например, дан график функции .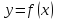

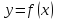
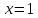
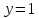
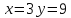
По графику функции можно узнать значение функции по выбранным значениям аргумента. Пусть . Находим на оси Ох координату, равную 1 и из этой точки проводим перпендикуляр до пересечения с графиком. Из точки пересечения проводим перпендикуляр к оси Оу и находим . Аналогично, при таким же способом находим . При . Точно также мы можем найти значение функции при любом выбранном значении аргумента.

При всей наглядности графического способа, у него есть существенные недостатки. На этом же графике видно, что если мы захотим выбрать не целое значение аргумента, а, например, , то точно найти это число на координатной оси проблематично, как также найти соответствующее значение . Значит, главным недостатком этого способа является сложность получения точных значений.

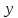
Рассмотрим теперь табличный способ задания функции и определим его преимущества и недостатки.

Этот способ задания функции чаще всего используется в практических целях, например, при замерах температуры наружного воздуха через определённые промежутки времени. Эта функция будет отображать зависимость температуры 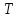от времени .

ч

Источник

Конспект урока на тему: «Графики функции» (7 класс)

Конспект урока по алгебре для 7 класса

на тему «График функции»

Тип урока: объяснение нового материала

1. Образовательная: ввести понятие «график функции», формирование умений строить график функции и читать его, формирование умений определять по графику соответствующие значения аргумента и функции.

2. Развивающая : способствовать развитию интеллектуальных навыков: сравнение, классификация, анализ; развитию коммуникативных навыков.

3. Воспитательная : воспитывать диалоговую культуру, любовь к предмету.

Устная работа. Фронтальная работа с классом

1.Приведите пример функциональной зависимомти одной переменной от другой.

Укажите независимую и зависимую переменные.

2.Как называется независимая переменная?

3.Как называется зависимая переменная?

4.Какие способы задания функции вы знаете?

6. Функция задана формулой у = 4 – 0,5х. Найдите значение аргумента, которому соответствует значение функции, равное 4.

7.Какие из графиков задают функцию?

3. Изучение нового материала

Фронтальная работа с классом.

(п.14 учебника до примера 1)

(определение графика функции стр.63)

Рассматриваем пример 1.

Коллективная выработка алгоритма построения графика функции:

По выбранным значениям одной величины (аргумента х) вычисляют значения другой величины (аргумента у)

На координатной плоскости отмечают точки с соответствующими координатами (х;у)

Полученные точки соединяют плавной линией.

4. Тренеровочное упражнение № 283 – на доске и в тетрадях

№ 286 – с комментарием

№ 287 – (работа в парах) с комментированием, оформление может быть дано в виде таблицы

-Что называется графиком функции?

-Что понравилось особенно?

-Что бы хотелось выполнить еще раз?

-Что не понравилось и почему?

-Что бы вы хотели изменить?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Конспект урока по алгебре для 7 класса на тему «Графикфункции»

Тип урока: объяснение нового материала

1.Образовательная: ввести понятие «график функции», формирование умений строить график функции и читать его, формирование умений определять по графику соответствующие значения аргумента и функции.

2.Развивающая: способствовать развитию интеллектуальных навыков: сравнение, классификация, анализ; развитию коммуникативных навыков.

3.Воспитательная: воспитывать диалоговую культуру, любовь к предмету.

Номер материала: ДБ-1193730

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В Думу внесли законопроект об обязательном образовании для находящихся в СИЗО подростков

Время чтения: 2 минуты

Петербургский Политех перевел студентов на дистанционку

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

«Функции и их графики» урок алгебры в 7 классе

Урок алгебры в 7 классе

Повторение темы: «Функция и их графики»

(Алгебра 7, Ю. Н. Макарычев и др.)

План разработки урока по теме « Функция и их графики» :

III. Оборудование урока.

IV. Организационный момент. Сообщение темы и цели урока.

V. Устная работа. Подготовка к обобщению ранее изученного материала. Математический диктант.

VI. Обобщение и систематизация теоретических знаний с помощью схем и таблиц.

VII. Выполнение тренировочных упражнений на уроке. Дифференциация заданий. Коллективная и индивидуальная деятельность учащихся.

VIII. Самостоятельная работа.

IX. Задание на дом. Объяснение домашнего задания (дифференциация).

X. Подведение итогов урока.

Повторение темы « Функции»

Образовательная : Актуализировать и обобщить знания по теме; повторить основные понятия и методы решения задач по теме; подготовить к итоговой проверке знаний;

организовать дифференциальную работу с учащимися на уроке;

развитие интереса и творческого подхода к изучению материала, используя методы проблемного обучения.

Требования к уровню подготовки учащихся:

Уметь: Находить значение функции по формуле для определенного аргумента; находить аргумент функции по ее известному значению; определять, принадлежит ли заданная своими координатами точка графику функции; составлять таблицу значений функции; строить графики функций y = kx и y = kx + e ; y = ;графически находить приближенное решение системы линейных уравнений.

Знать: Что такое функция, область определения функции, аргумент, зависимая и независимая переменные; что такое график функции. Какая функция называется линейной, что является графиком линейной функции. Какая функция называется прямой пропорциональностью, квадратичной функцией, что является их графиками. Как располагается график функции y = kx в зависимости от k в координатной плоскости. Условия пересечения и параллельности графиков линейных функций.

Сообщение темы и цели урока.

II. Фронтальная поверка домашнего задания.

1. Словарный диктант по теме «Функция».

Запишите математические термины:

Вариант 1 Вариант 2

1. Зависимость. 1. Функция.

2. Независимая переменная. 2. Аргумент.

3. Значение функции. 3. Область определения функции

4. График функции. 4. Зависимая переменная.

5. Координаты 5. Формула.

6. Абсцисса. 6. Ордината.

7. Линейная функция. 7. Прямая пропорциональность.

8. Прямая. 8. Начало координат.

9. Пересекаются. 9. Параллельные.

10. Взаимное расположение. 10. Угловой коэффициент.

Проверка диктанта проводится при обмене работ с содом по парте и сравнением с высветившимися на экране правильными записями.

I. Устная работа (проводится фронтально).

1. Выразите y через х:

II. Обобщение и систематизация теоретических знаний по теме:

Заслушивание доклада ученика, который он заранее подготовил к этому уроку.

Плакат: « Подобно тому, как дар слова обогащает нас мнением других, так язык математических законов служит средством еще более совершенным, более точным и ясным…»

( Проецируются портреты ученых: Виета, Декарта, Ньютона, Лейбница, Лобачевского).

Впервые термин «функция» использовал Готфрид Лейбниц (1646-1716).

Исаак Ньютон (1643-1727) рассматривал изменения физических величин в зависимости от времени. Рене Декарт (1596-1650) – изменение ординаты точки от изменения ординаты абсциссы, т.е. y от х. Николай Иванович Лобачевский (1792-7856) расширил понятие функции, используя способы задания функции: формулой, графиком или словесным испытанием.

Учитель обобщает материал по теме, используя таблицы, спроецированные на доску.

Таблица 1. Линейная функция y = kx + m (другое название: линейное уравнение с двумя переменными, формула, зависимость между х и y )

Линейная функция y = kx носит название « прямая пропорциональность».

Используя таблицу1 следует несколько раз повторить с учащимися различные формы записи и чертежа линейной функции.

Задание. Воспроизвести в тетрадях таблицу по памяти (черновые наброски).

Таблица 2. Взаимное расположение прямых на плоскости.

Таблица 3. Функция y = x 2 и ее график.

Парабола, вершина (0;0), ветви – вверх

По таблицам провести работу с учащимися следующим образом. Вызывать по очереди учащихся к доске и попросить прокомментировать обычными словами по 1 пункту каждой таблицы при активной поддержке класса.

Таблица 4. Общая запись функций.

III. Выполнение тренировочных заданий на уроке. Использованы материалы из «КИМ Алгебра-7» Мартышовой Л. И.

А2. Функция задана формулой х 2 +8- . Найдите значение функции, соответствующее значению аргумента, равному -3.

А3. Какая функция является прямой пропорциональностью?

А4. Укажите функцию, график которой параллелен графику функции y = x +5.

3) y =- x -1

4) y =-5 x +

В1. При каком значении числа k график функций y =3- x и y = kx +3 параллельны?

Работа проводится фронтально, устно, при активном объяснении учителя и обращая внимание учащихся на правильность и грамотность (математическую) речи учащихся.

Некоторые задания (А6; В2) учащиеся выполняют комментируя выполнение.

IV. Самостоятельная работа

(Проверку произвести, проектируя правильные ответы на экран)

1) Изобразите схематично графики функций

г) y =6 x +1 ; д) y =-3 x ; е) y =- ;

Можно учащимся объяснить, какое число выполняет параллельный перенос прямой вдоль оси ОУ.

2) Изобразите фигуру, ограниченную графиками функций.

Какая фигура получилась? Укажите координаты вершин полученной фигуры.

Укажите длину отрезка оси ординат, расположенного внутри этой фигуры.

3) При каком значении аргумента значение функции y = x 2 равно 25?

Проверка самостоятельной работы и ее выполнение проводится групповым методом.

V. Решение №361(б), №365 (а, в, г) фронтально у доски.

Подведение итогов урока.

Назовите названия известных вам функций, их формулы и графики соответственно.

Что такое аргумент? Функция?

VI. Домашнее задание записано на доске в самом начале урока. Учитель просит открыть учебники и делает пояснения по №361(в), №365 (б, д, е), №372 (б), №374, №378(б), №382.

Учащимся, проявляющим большой интерес к теме предлагаются к следующему уроку темы для докладов:

1. Понятие функции в математике до XVII в.

2. Функция вокруг нас.

3. Значение функции в жизни человека.

4. Функция в жизни физики и геометрии.

1. Учебник «Алгебра»/ Ю. Н. Макарычев и др. – М.: Просвещение, 2012

2. Поурочные разработки по алгебре. 7 класс/ А. Н. Рурукин и др. – М.: ВАКО, 2013.

3. Алгебра. Математические диктанты 7-9 классы / Конте А. С. – Волгоград: “Учитель”

4. КИМ. Алгебра.7класс. / Мартышова Л. И. – М.: ВАКО

5. Алгебра7, Блицопрос / Тульчинская Е. Е. – М.: Мнемозина, 2012

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Краткое описание документа:

Источник