Что такое графическое доказательство
законно ли графическое доказательство?
Для просмотра формул ваш браузер должен поддерживать MathML.
| Объявления | Последний пост | |
|---|---|---|
 | Senior lecturer in Mathematics Linkoping (Швеция) | 04.09.2021 23:16 |
 | Postdoc: Stochastics and algorithmics behind network problems (Netherlands) | 08.10.2021 08:36 |
 | Книги по математике и экономике в добрые руки! | 10.12.2021 10:59 |
Я вот о чём:
Некоторые задачи например теории вероятности
доказываются с помощью Диаграмм Вена (круговых схем).
Мне не понятно почему мы так легко переходим от доказательства с помощью формул, кванторов и т.д. к графическому доказательству?
Может мы описываем только узкий класс интуитивно понятных и графически представимых объектов?
Спасибо за внимание.
Кажется на лекции Успенского:
Доказательством мы называем такое рассуждение, поняв которое,
мы готовы убеждать в истинности доказываемого факта остальных 🙂
Разрешите несогласиться. И вот почему:
Не просто нужно, а жизненно необходимо.
Не зря старик Гильберт жизнь положил на создание метаматематических теорий. )))
P.S.: Гениальность Евклида состоит не в том, что он первым установил: «Диагональ круга делит его на две равные части» (это очевидно), а в том, что он первым попытался это доказать.
Цитата
Skald писал(а) :
Разрешите несогласиться. И вот почему:
Вы спутали два понятия: доказательства и иллюстрации к доказательству.
Иначе грош цена такому доказательству: «на глазок» я могу сказать, что диагонали квадрата пересекаются под прямым углом. А вот вы докажите, что мне это не кажется. В этом и состоит назначение математического аппарата теории доказательств. Без него никуда.
Вы совершенно правы в примере с квадратом: если что-то мне почудилось на чертеже, это еще не доказательство. Не потому, что догадка неверна, а потому, что я сам не могу перевести ее на формальный язык.
Разумеется, в формально-логическом смысле «законен» только строгий аксиоматический вывод. Таким образом, ни одно доказательство ни в одной математической работе (исключая учебник логики) не является законным: ведь там, кроме формул, используются еще и слова!
Математики, однако, привыкли называть доказательством нечто другое. А именно, любой текст, который подготовленный читатель может самостоятельно перевести на язык формул. Не важно, написан ли этот текст по-английски или представляет собой картинку из нескольких пересекающихся кружочков: главное, чтобы каждый математик воспринимал его однозначно!
. Чувствуется скрытая цитата из уважаемого мною (и, надеюсь, Вами) проф. Успенского. Тут не поспоришь. )))
А вот это уже логическая ошибка.
Действительно, доказательство суть текст.
Но текст н е суть доказательство.
Текст я могу воспринимать также как и Вы*. Возможно. Но является ли этот текст доказательством н е зависит от этого факта.
Пример: «диагонали квадрата пересекаются под прямым углом». Я могу нарисовать этот факт, рассказать о нём по-английски (или по-русски), изобразить, наконец, посредством пантомимы. При этом масса людей воспримет мои действия одинаково. Но это обстоятельство не докажет истинности высказывания о диагоналях квадрата.
. Чувствуется скрытая цитата из уважаемого мною (и, надеюсь, Вами) проф. Успенского. Тут не поспоришь. )))
Если Вы согласились с первым тезисом (цитату из Успенского не помню, но, видимо, большинство математиков так считают), то как можно спорить со вторым?
Не так с квадратом, диагонали которого Вы изображаете посредством пантомимы. Все поймут: Вы уверены в том, что угол между ними прямой. Тем самым, Ваше сообщение будет вполне однозначно (и законно) воспринято как гипотеза, а не доказательство.
PS А к профессору Успенскому я испытываю двойственные чувства. 😉
Графическое доказательство
Для построения графического доказательства необходимо изобразить на диаграмме Эйлера-Венна все множества, входящие в тождество таким образом, что бы присутствовали их все возможные пересечения, после чего построить результат операций левой и правой частей тождества.
Например, докажем тождество
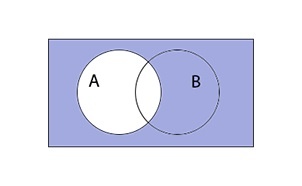
1) Диаграмма левой части:
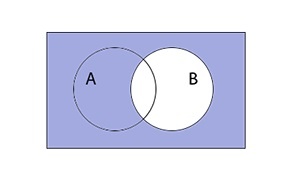
2) Диаграмма правой части:
Как видно из рисунка, результат операции левой и правой частей совпадают, следовательно тождество верно.
Выполнение графических построений для 4 и более множеств проблематично.
2. Доказательство взаимного включения множеств (доказательство «если-то»)
1) Докажем что первое множество полностью лежит во втором
2) В обратную сторону:
Эта тема принадлежит разделу:
Порядок записи элементов множества не является существенным в отличие от записи элементов векторов, где порядок важен
Множество это совокупность определ нных различаемых объектов прич м таких что для каждого можно установить принадлежит этот объект данному.. множества обычно обозначаются заглавными латинскими буквами а элементы.. например..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Графическое доказательство
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Характеристическая функция
Характеристическая функцияили индикатор показывает принадлежность элементов множеству (обозначается или ). Характеристическая функция пуст
Пустое отношение
Операции на отношениях: Пересечение Объединение Произведение Дополнение: Обратное отношение к R:
Формулы алгебры логики
Атомарные высказывания обозначаются маленькими буквами и называются пропозициональными (или булевыми) переменными. Формулы алгебры логики называются пропозициональные формулы. Формулой явл
Таблицы истинности
Логическое значение формулы определяется заданными логическими значениями входящих в неё элементарных высказываний. Пример. x1=1, x2=1, x3=0. Определить значение формулы
Равносильные формулы
Две формулы алгебры логики называются равносильными, если они принимают одинаковые логические значения при любом наборе значений элементарных высказываний, входящих в
Полные системы функций (связок)
Система функций является полной, если любая n-арная булева функция может быть записана в виде пропозициональной формулы с использованием только функций входящих в эту систему. Систе
Дизъюнктивные и конъюнктивные нормальные формы
Элементарной конъюнкцией называется конъюнкция переменных высказываний и (или) их отрицаний. Например: Элементарной дизъюнкциейназываетс
Теорема о тождественной истинности формулы алгебры логики
Для того, чтобы формула алгебры логики была тождественно истиной, необходимо и достаточно, чтобы каждая элементарная дизъюнкция её конъюнктивной нормальной формы содержала, по крайней мере, одно эл
Теорема о тождественной ложности формулы алгебры логики
Для того, чтобы формула алгебры логики была тождественно ложной, необходимо и достаточно, чтобы каждая элементарная конъюнкция её ДНФ содержала по крайней мере одно элементарное переменное высказыв
Совершенные нормальные формы
Совершенная дизъюнктивная нормальная форма. Элементарная конъюнкция называется правильной,если в неё каждая переменная входит не более одного раза,
Построения СДНФ и СКНФ
Построение СДНФ: 1. Преобразование исходной формулы в ДНФ (см выше): Шаг 1. Преобразовать исходную формулу к равносильному ей виду
Построение совершенных нормальных форм с помощью таблиц истинности
Для построения СДНФ или СКНФ, исходя из теоремы о разложении функции алгебры логики от n переменных по k переменным (k=n), можно воспользоваться таблицами истинности. Для построения
Разложение функций алгебры логики по к переменным
Теорема. Всякую логическую функцию f(x)=f(x1,x2,x3,…,xn) можно представить в виде
Тавтологии и противоречия. Проблема разрешимости в алгебре логики. Логические следствия
Формула алгебры логики называется тождественно истиной, общезначимой или тавтологией,если она принимает значение 1 п
Теорема о тождественной истинности формулы алгебры логики
Для того, чтобы формула алгебры логики была тождественно истиной, необходимо и достаточно, чтобы каждая элементарная дизъюнкция её конъюнктивной нормальной формы содержала, по крайней мере, одно эл
Теорема о тождественной ложности формулы алгебры логики
Для того, чтобы формула алгебры логики была тождественно ложной, необходимо и достаточно, чтобы каждая элементарная конъюнкция её ДНФ содержала по крайней мере одно элементарное переменное высказыв
Теорема о логическом следствии
Формула алгебры логики f является логическим следствием формулы алгебры логики g,тогда и только тогда, если g f. Доказательство.
Минимизация функций алгебры логики. Каноническая постановка задачи минимизации. Этапы минимизации. Методы минимизации
Минимизация функций алгебры логики (ФАЛ) – это процедура нахождения наиболее простого представления ФАЛ в виде суперпозиции функций, составляющих фун
Методы минимизации
К настоящему времени широкое применение получили: 1. Расчетный метод (метод непосредственных преобразований). 2. Расчетно-табличный метод (метод Квайна-МакКласки). 3. Мет
Исчисление предикатов
Наибольшее распространение в системах искусственного интеллекта получила формальная система, носящая название исчисления предикатов первого порядка (ИППП). Алфавит ИППП состо
Значение формулы логики предикатов
О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество M, на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики преди
Описание машины Тьюринга
Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj&
Диаграммы Эйлера-Венна
Что такое диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
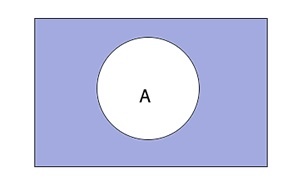
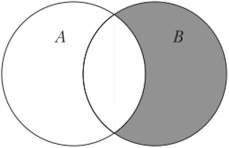
Дополнение множества
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
Таким образом выглядит дополнение \(\overline A\) графически:
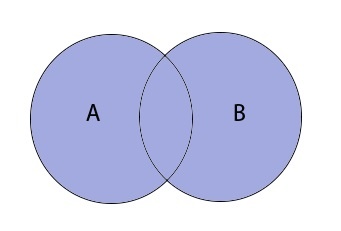
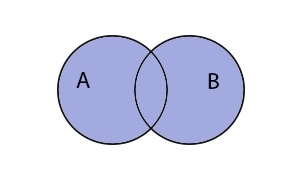
Объединение множеств
Объединение записывается следующим образом:
Таким образом объединение множеств выглядит графически:
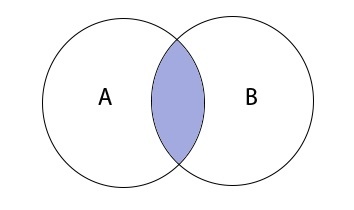
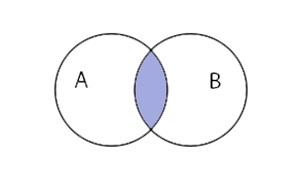
Пересечение множеств
Пересечение множеств записывается следующим образом:
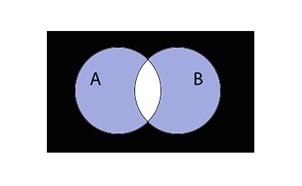
Таким образом пересечение множеств выглядит графически:
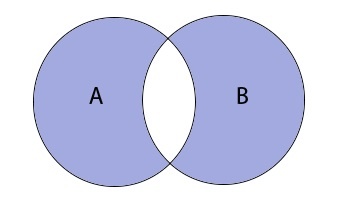
Симметричная разность множеств
Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)
Таким образом разность выглядит графически:
Разность множеств
Разностью A \ B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
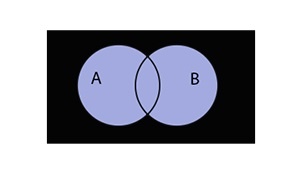
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
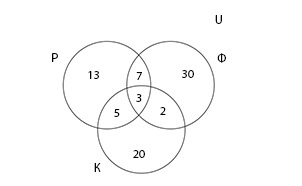
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
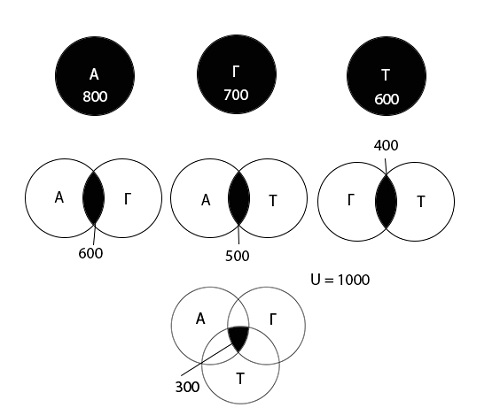
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
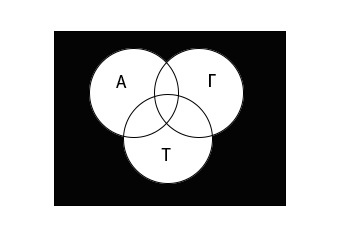
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
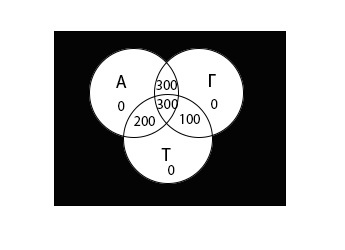
Теперь внесем значения всех областей в диаграмму:
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
Ответ: 100 школьников не решило ни одной задачи.
Графическое доказательство
Для построения графического доказательства необходимо изобразить на диаграмме Эйлера-Венна все множества, входящие в тождество таким образом, что бы присутствовали их все возможные пересечения, после чего построить результат операций левой и правой частей тождества.
Например, докажем тождество
1) Диаграмма левой части:
2) Диаграмма правой части:
Как видно из рисунка, результат операции левой и правой частей совпадают, следовательно тождество верно.
Выполнение графических построений для 4 и более множеств проблематично.
2. Доказательство взаимного включения множеств (доказательство «если-то»)
Докажем что
1) Докажем что первое множество полностью лежит во втором

таким образом
2) В обратную сторону:
таким образом
3) Так как 

Что такое графическое доказательство
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность: