Что такое граф в моделировании
Использование графов в моделировании
Вы будете перенаправлены на Автор24
Графические модели
Графических моделей достаточно много. Рассмотрим основные из них.
Графы являются наглядным средством отображения состава и структуры системы.
Например, есть словесное описание определенной местности: «Район состоит из пяти поселков: Дорожное, Булавино, Рудино, Крылово и Медвежье. Автомобильные дороги ведут от Дорожного к Булавино, от Дорожного к Крылово, от Булавино к Медвежьему, от Булавино к Крылово, от Крылово к Рудино». По такому описанию очень сложно представить такую местность. Такую информацию гораздо легче воспринимать с помощью схемы. Эта схема не является картой местности, в ней не выдержаны направления по сторонам света, не соблюдается масштаб. На схеме отражены лишь пять поселков и дорожная связь между ними. Схема, которая отображает элементный состав системы и структуру связей, называется графом.
Составными частями графа являются вершины и ребра. Вершины изображаются кругами – это элементы системы, а ребра изображаются с помощью линий – связей (отношений) между элементами. С помощью такого графа можно легко разобраться в структуре дорожной связи данного района.
Готовые работы на аналогичную тему
Можно построить граф, который будет содержать количественные характеристики. В таком случае возле ребер графа можно проставить числа, которые обозначают длины дорог в километрах. Такой граф называется взвешенным. Взвешенный граф может содержать количественные характеристики связей и вершин. Например, количественной характеристикой вершины может быть население поселка. По взвешенному графу можно определить, что второй путь короче первого.
На рассмотренных графах каждое ребро указывает на наличие дорожной связи между двумя пунктами, которая действует одинаково в обе стороны: если по данной дороге можно проехать от Булавино к Медвежьему, то по ней можно проехать и от Медвежьего к Булавино (предполагается, что действует двустороннее движение). Такие графы называются неориентированными, а их связи – симметричными.
Рассмотри граф, который относится к медицине и показывает совместимость групп крови.
Известно, что кровь каждого человека отличается по группе, которых существует четыре вида. Для переливания крови одного человека другому не все группы подходят. Граф отображает возможные варианты переливания крови. Группы крови – это вершины графа с соответствующими номерами, а стрелки показывают возможность переливания одной группы крови человеку с другой группой крови. Например, по графу можно определить, что кровь I-й группы подходит любому человеку, а человеку с I-й группой крови можно переливать только кровь своей группы; человеку с IV-й группой крови можно переливать любую, а его собственная кровь подходит только человеку с той же группой.
Связи между вершинами данного графа являются несимметричными и поэтому изображены с помощью направленных линий со стрелками. Такие линии называют дугами (а у неориентированных графов – ребрами). Граф с такими свойствами называется ориентированным. Линия, которая выходит и входит в одну и ту же вершину, называется петлей. На данной графе изображены четыре петли.
Таким образом, преимущества изображения модели системы переливания крови в виде графа неоспоримы в сравнении со словесным описанием тех же правил. Граф легко воспринимается и запоминается.
Дерево – граф иерархической структуры
Системы с иерархической структурой являются весьма распространенным типом систем. Иерархическая структура образуется, когда объекты или какие-либо их свойства находятся в отношении подчинения (вложения, наследования). Обычно иерархическая структура присуща системам административного управления, между элементами которых установлены отношения подчиненности. Например: директор организации – начальники отделов – сотрудники. Системы, между элементами которых существуют отношения вхождения одних в другие, также имеют иерархическую структуру.
Граф иерархической структуры называют деревом. Основным свойством такого графа является то, что между любыми двумя его вершинами существует единственный путь. У деревьев нет циклов и петель.
Рассмотрим граф, который отражает иерархическую административную структуру Российской Федерации: государство содержит 7 административных округов; округа делятся на регионы (области и национальные республики), в состав которых входят населенные пункты. Такой граф представляет собой дерево.
Дерево имеет одну главную вершину, называемую корнем дерева. Такая вершина изображается вверху, а от нее проходят ветви дерева. Начиная от корня идет отсчет уровней дерева. Вершины, которые непосредственно связаны с корнем, являются вершинами первого уровня. От них идут ветви к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин следующего уровня. Такой вид связи называется «один ко многим». Вершины, не имеющие порожденных, называются листьями. На данном дереве листьями являются вершины, которые обозначают города.
Графические информационные модели. Графы
Урок 6. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Графические информационные модели. Графы»
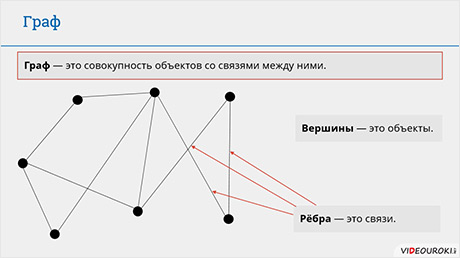
Граф – это совокупность объектов со связями между ними. Графически это будет выглядеть следующим образом:
Вершины (точки) – это объекты, а ребра (линии между ними) – это связи. Помимо точек вершины графа могут изображаться овалами, кругами, прямоугольниками и так далее. Связи между вершинами могут быть различными: дуги, рёбра, петли.
На данном уроке мы с вами познакомимся с ориентированными и неориентированными графами. В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.
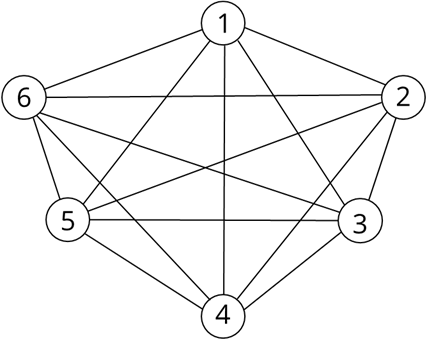
Решим задачу: В соревнованиях по шахматам участвовало 6 учащихся с 9 по 11 класс. При встрече они все обменялись рукопожатиями. Вопрос: сколько всего было сделано рукопожатий?
Для решения данной задачи будем использовать граф. Вершинами графов будут являться шесть учащихся, которые участвовали в турнире. Пронумеруем их от одного до шести. Проведем от каждой вершины линии (ребра) к оставшимся пяти вершинам.
Для ответа на вопрос остается сосчитать, сколько линий изображено на графе. Ответ: на турнире было сделано 15 рукопожатий.
Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
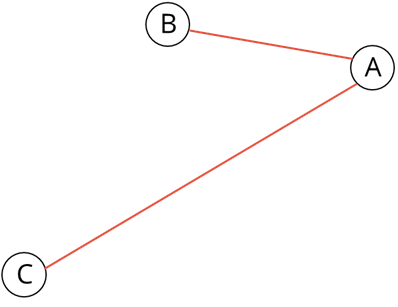
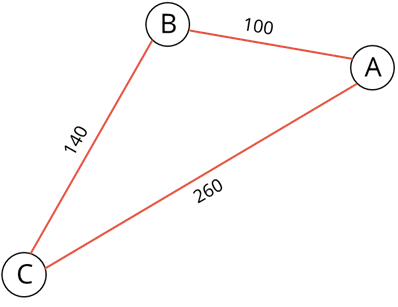
Давайте сами нарисуем взвешенный граф на основе задачи со следующим условием: Между городами A, B, C, D, Е построены дороги. Необходимо найти кратчайший путь из города А в город Е, если известно, что из города А в город В расстояние 100 километров, из А в С – 260 километров, из В в С – 140 километров, из В в Е – 400 километров, из С в D – 50 километров, из С в Е – 100 километров и из D в Е – 40 километров.
Итак, для решения данной задачи необходимо нарисовать взвешенный граф, так как нам дано расстояние, то есть вес рёбер. Для начала нарисуем вершину А. Из неё будут выходить два ребра в вершины В и С. Ребро из А в В будет короче, чем из А в С, так как расстояние из пункта А в пункт В 100 километров, а из пункта А в пункт С – 260 километров.
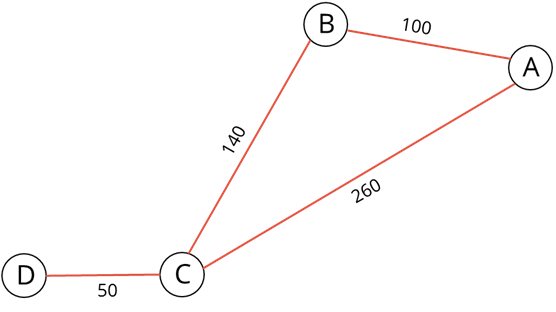
Далее нарисуем ребро из В в С и его вес будет равен 140.
Теперь нарисуем ребро из вершины С в вершину D и укажем вес 50
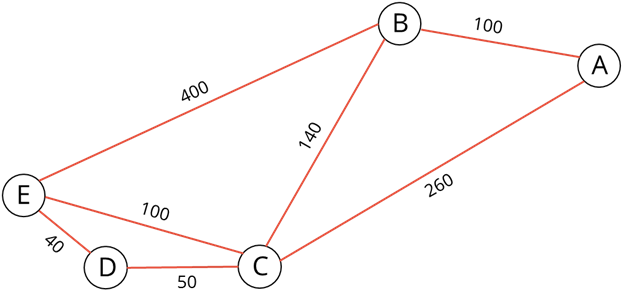
У нас получился взвешенный граф.
Нам осталось найти кратчайший путь. Для этого из вершины А будем идти в вершину В – это 100 километров, затем сразу в вершину Е. Слаживаем 100 и 400, получим 500 километров.
В свою очередь, цикл – это цепь, в которой начальная и конечная вершины совпадают. В детстве, наверное, каждый из вас рисовал звезду, не отрывая ручки от бумаги и не проходя дважды по одной и той же линии или ребру. При изображении такой звезды начальная и конечная вершины совпадают. Сеть – это граф с циклом.
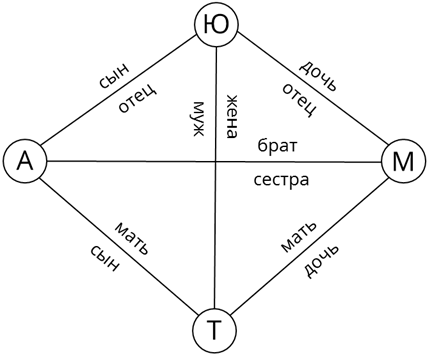
Разберём ещё один пример. У Антона в семье есть мама Татьяна, папа Юрий и сестра Маша. Изобразим каждого члена семьи как вершину нашего графа и обозначим первыми буквами имён. От каждого из них проведём рёбра к оставшимся троим. Над каждым из рёбер укажем, кто кем и кому приходится. Например, если идти от вершины Антона к Юрию, то Антон является сыном. А если идти наоборот, от Юрия к Антону, то Юрий является отцом. Аналогичным образом можно провести отношения между всеми членами семьи. Данный граф является примером семантической, или же смысловой сети.
Таким образом, Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними. Все связи данного графа различны, поэтому их необходимо подписывать.
Графы широко распространены как информационные модели. Их можно применять, например, при планировании жилого района, где вершинами будут являться дома, а рёбрами – дороги или дорожки, которые их связывают. Ещё одним примером будет являться карта проезда по городу на любом из видов транспорта, где остановки – это вершины, а путь движения транспорта – это рёбра и так далее.
Следующее определение в данной теме: дерево. Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь. Корень дерева – это одна и единственная главная его вершина.
Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков. Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Листья – это вершины, которые не имеют потомков.
Разберёмся более подробно на примере:
Ученик Антон решил составить генеалогическое дерево своей семьи. Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он является сыном своего отца Юрия и мамы Татьяны. В свою очередь Татьяна является дочерью Леонида (дедушки Антона) и Елены (бабушки Антона). Юрий является сыном Григория (дедушки Антона) и Марии (бабушки Антона). У Антона есть сестра Маша. Так как словесное описание трудно для восприятия, давайте поможем Антону представить это все в виде дерева и построим генеалогическое дерево.
Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху. У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок. У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.
Таким образом, мы построили родословное дерево.
· Граф – это совокупность объектов со связями между ними.
· Вершины – это объекты, а ребра – это связи.
· Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
· Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза.
· Цикл – это цепь, в которой начальная и конечная вершины совпадают.
· Сеть – это граф с циклом.
· Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними.
· Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину.
Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Вторым признаком является отсутствие или наличие кратных ребер.

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Что такое граф в моделировании
Наглядным средством представления состава и структуры системы является граф. Граф состоит из вершин,связанных линиями. Линия со стрелкой называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей. Вершины могут изображаться овалами, прямоугольниками и т. д.
Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель рассматриваемой системы в форме графа.
Ранее мы рассматривали графы — схемы отношений, отражающие имеющиеся связи между объектами.
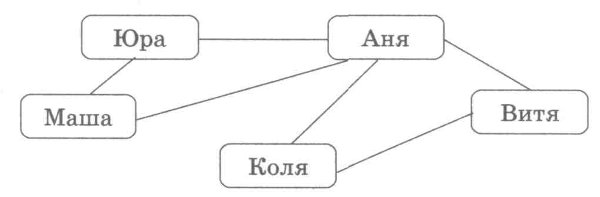
Например, граф, отражающий отношение «переписываются» между объектами класса «дети», может выглядеть, как показано на рис. 2.28.
Отношение «переписываются» («пишут письма друг другу») является двухсторонним (симметричным). Поэтому соответствующие вершины соединены линиями без стрелок (ребрами). Граф называется неориентированным, если его вершины соединены ребрами.
Путь по вершинам и ребрам графа, включающий любое ребро графа не более одного раза, называется цепью.
Пример цепи: Юра — Аня — Витя — Коля.
Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Пример цикла: Аня — Коля — Витя — Аня.
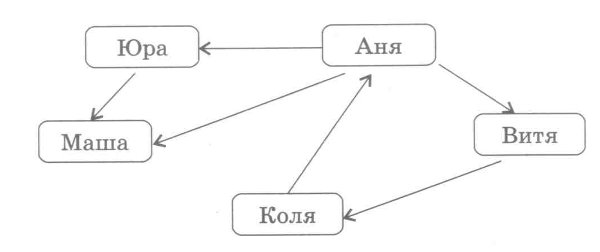
Иначе выглядит граф, отражающий отношение «пишет письма» между теми же объектами класса «дети». Линии со стрелками (дуги) придают ему совершенно иной смысл (рис. 2.29).
Граф называется ориентированным, если его вершины соединены дугами.
Приведите примеры цепи и цикла в графе на рис. 2.29.
Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).
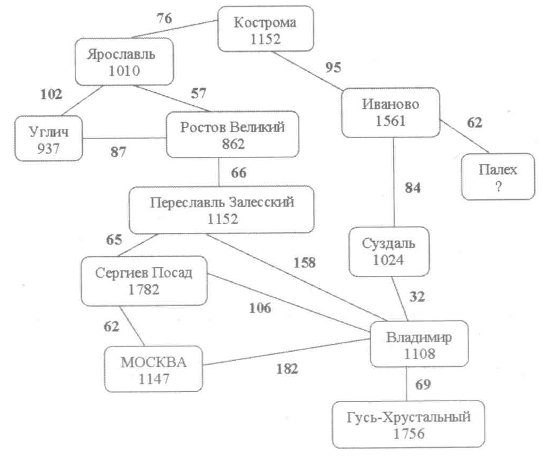
На рис. 2.30 информация о городах Золотого кольца представлена взвешенным графом: веса его вершин — года основания городов, веса ребер — расстояния в километрах между городами.
Назовите пути и циклы в графе на рис. 2.30.
Граф с циклом называется сетью.
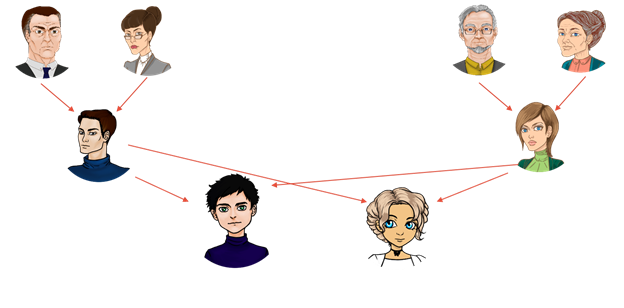
На рис. 2.31 в виде графа представлена информационная модель сказки про Царевну-лягушку.
Информатика. 11 класс
Конспект урока
Информатика, 11 класс. Урок № 7.
Тема — Моделирование на графах
Цели и задачи урока:
На уроке вы узнаете:
Давайте рассмотрим, пожалуй, самую известную головоломку, придуманную аж в XVIII веке, и захватившую умы человечества на многие годы. Называется она задача о семи Кёнигсбергских мостах. В Кёнигсберге начиная с XIV было построено 7 мостов: Медовый мост, Лавочный мост, Зелёный мост, Рабочий мост, Кузнечный мост, Деревянный мост и Высокий мост, соединяющий остров и полуострова в единый город. Тогда и возникла головоломка: «Как пройти по всем мостам, не проходя ни по одному дважды?»
Десятилетиям жители города пытались решить эту задачу как практически (гуляя по городу), так и теоретически.
И только Леонард Эйлер, введя новое понятие — ГРАФ, смог решить ее раз и навсегда.
Граф — абстрактный математический объект, представляющий собой множество вершин графа (обозначены красным цветом) и набор рёбер (обозначены синим), то есть соединений между парами вершин. При этом каждое ребро представляет собой отношение двух вершин.
— Неориентированные и ориентированные (когда движение по ребру возможно только в одну сторону).
— Взвешенными (когда у вершины или у ребра есть вес, отличающий его от другого) и невзвешенный.
— И другие более сложные графы (мультиграф, псевдограф, изоморфный граф и другие).
Эйлер установил, что:
1. Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно или не может существовать граф, который имел бы нечётное число нечётных вершин.
2. Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
3. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
ВЫВОД: пройти только один раз по каждому мосту невозможно.
Графы находят широкое применение во многих сферах нашей жизни. Например, с их помощью можно планировать оптимальные транспортные маршруты, упростить решение математических задач, визуализировать решения компьютерных программ, визуализировать различную информацию (схема метро, карта звездного неба и т. д.).
Очень часто для решения задач требуется найти кратчайший путь между двумя вершинами.
Кратчайшим путем мы будем называть путь, если: эти вершины соединены минимальным числом ребер (в случае, если граф невзвешенный); сумма ребер, соединяющих эти вершины, минимальна (для взвешенного графа).
Существует огромное количество алгоритмов, находящих кратчайший путь и один из них — это алгоритм Дейсктры.
Алгоритм заключается в том, что надо пошагово перебрать все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.
Для примера возьмем следующий взвешенный ориентированный граф и попытаемся найти кратчайший путь от вершины A до F. Пошагово переберём все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.
Первым шагом: присвоим вершине А метку равную 0, потому как эта вершина — начало. Остальным вершинам присвоим метки равные бесконечности.
Вторым шагом: выберем не вычеркнутую вершину, вес которой является минимальным («источник»). Сейчас это вершина А. Вычисляем сумму веса вершины источника и веса ребра
Если она окажется меньше веса вершины приемника, то изменим вес этой вершины.
Третьим шагом: вычеркнем вершину-«источник».
Повторим шаги 1, 2, 3 до тех пор, пока не будут вычеркнуты все вершины.
Еще один способом нахождения кратчайшего пути может служить «метод динамического программирования».
Пусть дан некоторый лабиринт, соединяющий комнаты в виде графа. При этом заходя в каждую комнату, нужно заплатить пошлину. Необходимо пройти по нему от точки А до точки В, потратив наименьшее количество денег.
Составим таблицу, в которой каждая ячейка будет соответствовать определенной ячейке. Числа в ячейках будут равны минимальному числу пошлины, которое можно получить, пройдя от начала (A) до соответствующей клетки.