Что такое граф смежности
Теория Графов. Часть 2 Смежность, инцидентность, петли
Ничего не сделано, если что-то осталось недоделанным. – Иоганн Гаусс
Смежность и инцидентность
Смежность и инцидентность
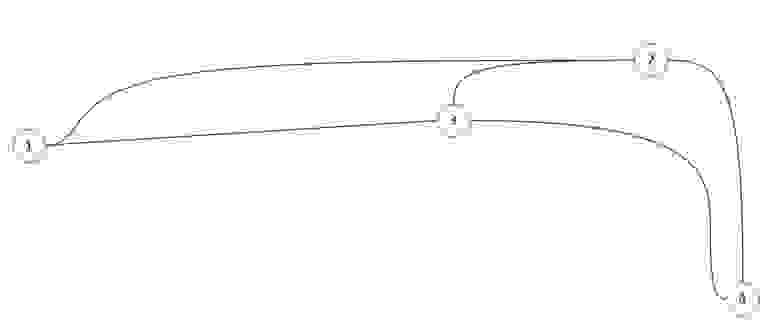
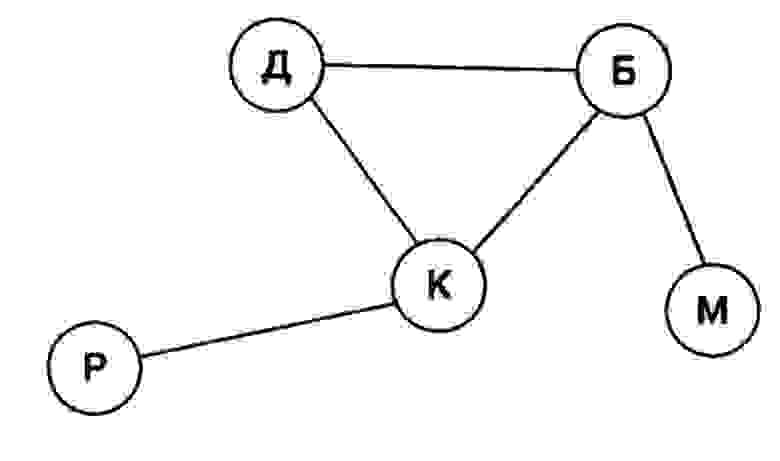
Давайте рассмотрим самый обыкновенный неориентированный граф (Рисунок 1). В нем есть вершина Р и вершина К. Данные вершины являются смежными (adjacent), так как они соединены ребром РК.
Помимо этого, как мы видим, вершина К является концом ребра РК, а Р его началом, в таких случаях вершина К и Р называются инцидентными (incident) ребру РК.
Смежностью вершин графа – называется отношение между двумя вершинами, в котором существует ребро их соединяющее.
Инцидентность – это когда вершина a является началом или концом ребра t. Если мы добавим еще одну вершину b, то мы скажем, что вершина a и b инцидента ребру t.
Кроме вершин, смежность присутствует и у рёбер. Рёбра просто должны иметь общую вершину. В нашем случаи мы можем сказать, что ребро ДК является смежным ребру РК, так как у них есть общая вершина К.
Смежностью рёбер графа – называется отношение между двумя рёбрами, в котором существует вершина соединяющая их.
В связи с тем, что выше мы рассматривали неориентированный граф, то было неважно, с какого направления определять смежность и инцидентность. Вершина Р могла быть смежна вершине К, но также мы могли сказать, что вершина К смежна вершине Р.
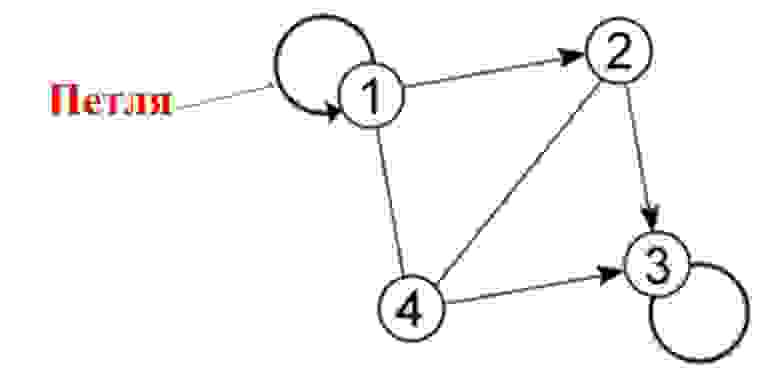
В ориентированном графе все немного по-другому (Рисунок 2), так у нас имеется направление, которое мы не в силах поменять. Если вершина 1 смежна вершине 2, то вершина 2 не может быть смежна вершине 1. То же самое касается и инцидентности. Вершины 1 и 2 инцидентны ребру 12, наоборот не работает.

Петли
Петля – это ребро инцидентное одной и той же вершине. То есть вершина которая соединена сама с собой. На рисунке ниже мы видим, как это выглядит.
Заключение
В следующей статье я покажу, как с помощью матрицы задавать графы, а также покажу, что такое вес ребра.
Графы: основы теории, алгоритмы поиска
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Графы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Теория графов. Часть третья (Представление графа с помощью матриц смежности, инцидентности и списков смежности)
Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор
Список смежности (инцидентности)
Взвешенный граф (коротко)
Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.
Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).
Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).
Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.
Матрица смежности
Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.
Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.
Каждая ячейка матрицы равна либо 1, либо 0;
Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.
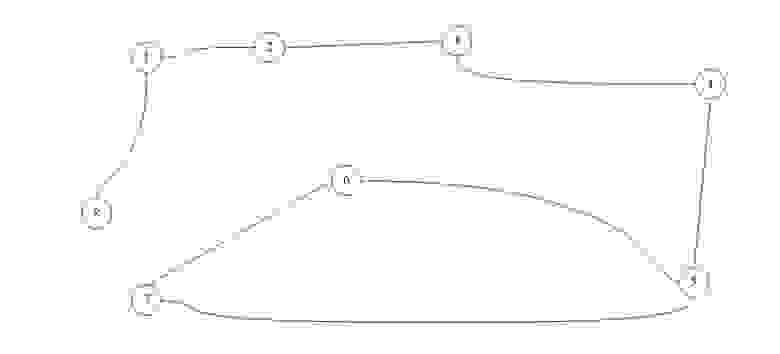
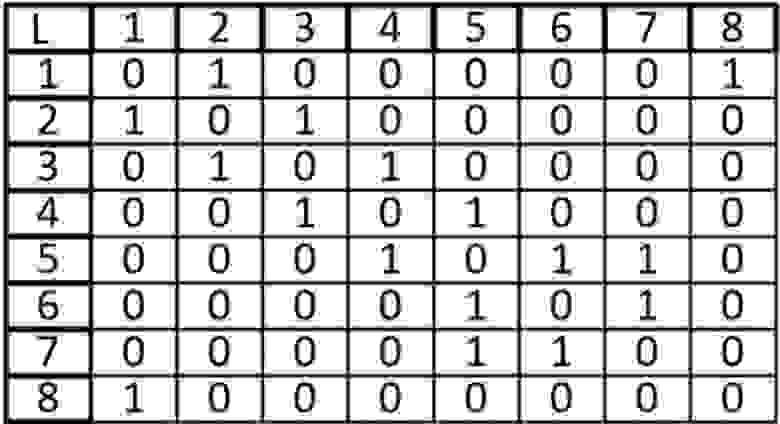
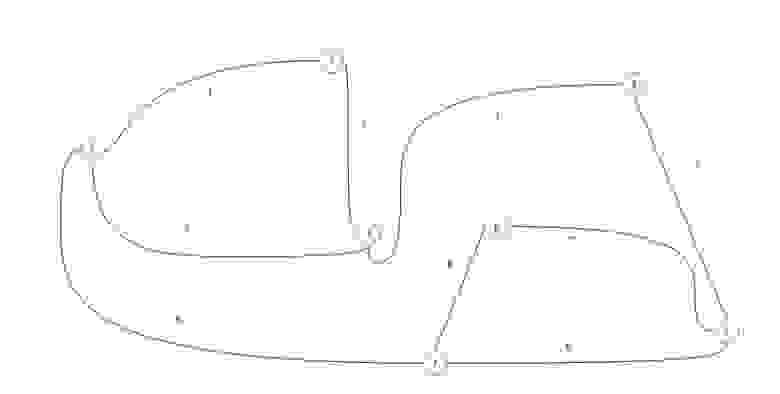
Для практического примера возьмем самый обыкновенный неориентированный граф:
А теперь представим его в виде матрицы:
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.
С одной стороны объем памяти будет:
Но используя вышеописанный подход получается:
Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.
Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
Если мы используем ориентированный граф, то кое-что меняется.
Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.
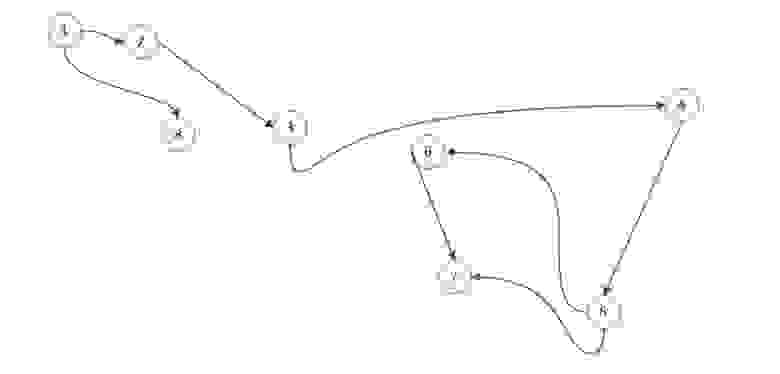
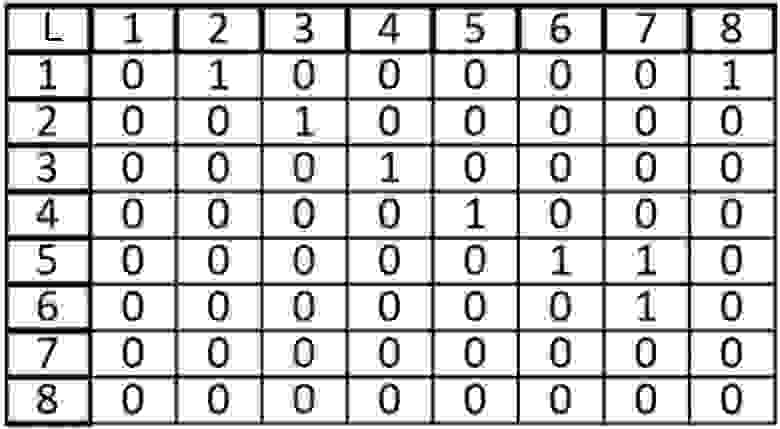
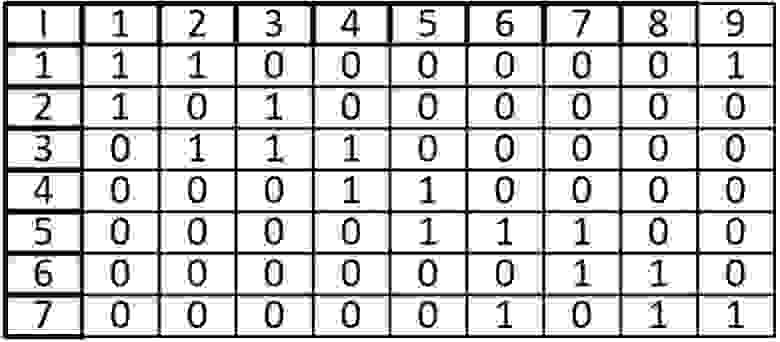
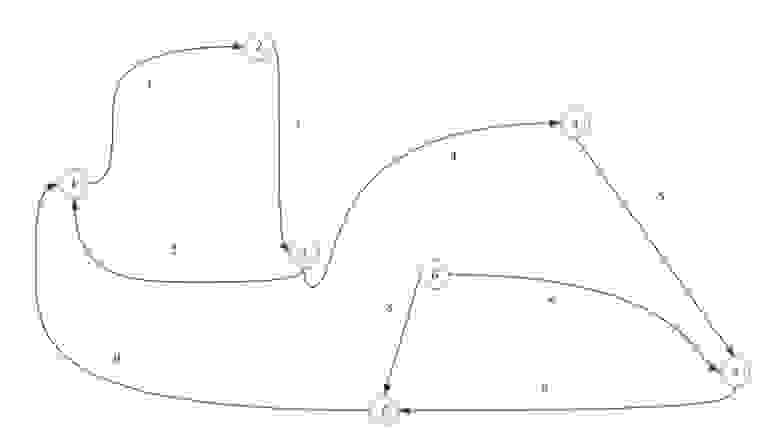
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:
Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.
Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.
Матрица инцидентности
Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.
Сразу же иллюстрируем данное правило:
Сумма элементов i-ой строки равна степени вершины.
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.
Список смежности (инцидентности)
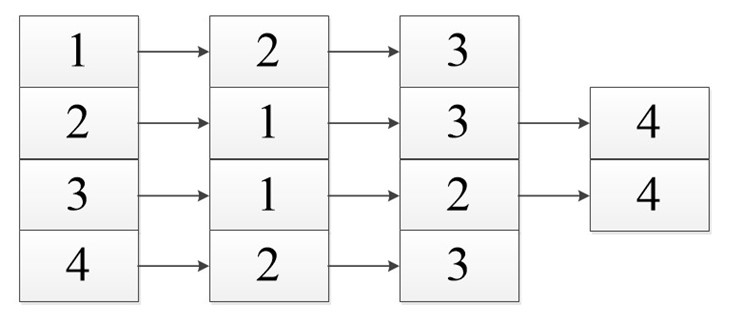
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.
В виде списка это будет выглядеть так:
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.
Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:
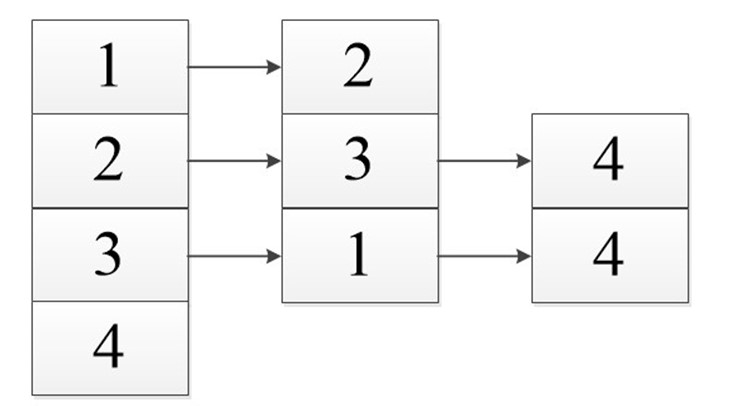
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).
Сумма длин всех списков:
Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.
К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.
Взвешенность графа
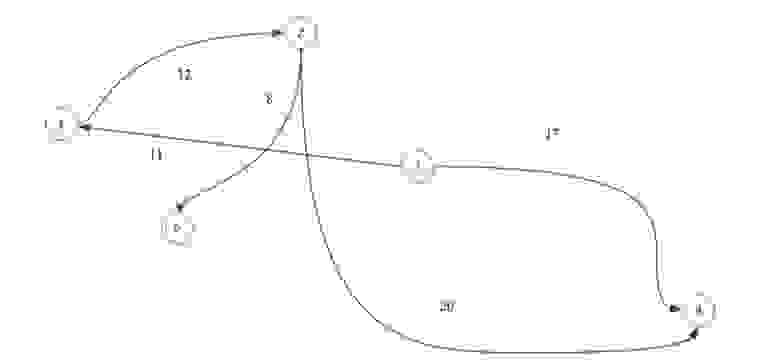
К примеру, возьмем граф с весами на ребрах:
И сделаем матрицу смежности:
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.
Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.
Если заметили ошибку или есть предложения пишите в комментарии.
Графы: основы теории, алгоритмы поиска
Aug 22, 2020 · 6 min read
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Г р афы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Инцидентность и смежность в графах, матрицы смежности, матрицы инцидентности, списки инцидентности
Инцидентность вершин и рёбер графа, смежность вершин графа
Пример 1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)
Итак, задаём граф следующими множествами:
Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте. При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.
В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.
Матрицы смежности
Матрица смежности для неориентированного графа
Элемент матрицы смежности s ij неориентированного графа определяется следующим образом:
— равен единице, если вершины v i и v j смежны;
— равен нулю, если вершины v i и v j не смежны.
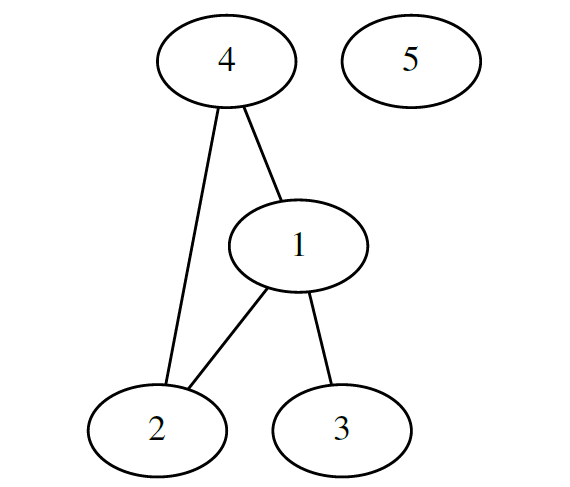
Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.
Матрица смежности для ориентированного графа
Элемент матрицы смежности s ij ориентированного графа определяется следующим образом:
— равен единице, если из вершины v i в вершину v j входит дуга;
— равен нулю, если из вершины v i в вершину v j дуга не входит.
Пример 3. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Таким образом, матрица смежности ориентированного графа не симметрична.
Матрица смежности для графа с кратными рёбрами
Пример 4. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 2 | 0 | 0 |
| 2 | 3 | 0 | 0 | 1 | 1 |
| 3 | 2 | 0 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Матрица смежности для взвешенного графа
В случае взвешенного графа элемент матрицы смежности s ij равен числу w, если существует ребро между вершинами v i и v j с весом w. Элемент s ij равен нулю, если рёбер между вершинами v i и v j не существует.
Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.
| V | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 11 | 9 | 0 | 0 |
| 2 | 11 | 0 | 0 | 5 | 8 |
| 3 | 9 | 0 | 0 | 0 | 2 |
| 4 | 0 | 5 | 0 | 0 | 0 |
| 5 | 0 | 8 | 2 | 0 | 0 |
Матрицы инцидентности
Матрица инцидентности для неориентированного графа
Элемент матрицы инцидентности для неориентированного графа h ij определяется следующим образом:
— равен единице, если вершина v i инцидентна ребру e j ;
Пример 6. Составить матрицу инцидентности для графа, представленного на рисунке ниже.
| V | 1-2 | 1-3 | 2-4 | 2-5 | 3-5 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 |
Матрица инцидентности для ориентированного графа
Элемент матрицы инцидентности для ориентированного графа h ij определяется следующим образом:
— равен минус единице, если вершина v i является началом ребра e j ;
— равен единице, если вершина v i является концом ребра e j ;
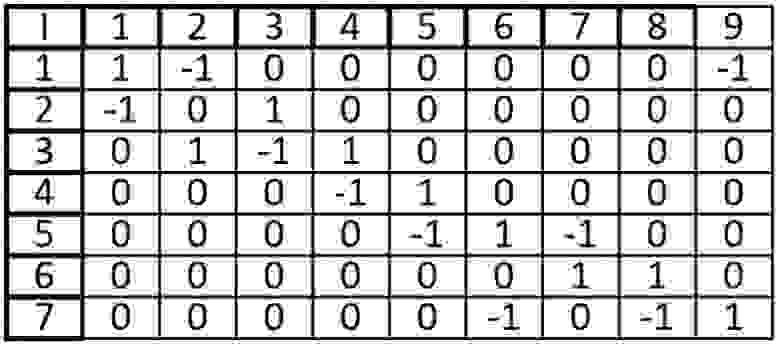
Пример 7. Составить матрицу инцидентности для графа, представленного на рисунке ниже.
| V | 1-2 | 1-3 | 2-4 | 2-5 | 3-5 |
| 1 | 1 | -1 | 0 | 0 | 0 |
| 2 | -1 | 0 | -1 | -1 | 0 |
| 3 | 0 | 1 | 0 | 0 | -1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 |
Списки инцидентности
Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.
Список инцидентности одной вершины графа включает номера вершин, смежных с ней.
Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.
Пример 8. Составить списки инцидентности для графа, представленного на рисунке ниже.
Преимущества и недостатки каждого способа
Матрицы смежности и инцидентности целесообразнее использовать когда:
Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.
Списки инцидентности целесообразнее использовать когда:
На практике списки чаще используются в прикладных целях.