Что такое граф материалы
Граф: что это такое в математике, какие существуют его виды и другое
Содержание:
Граф — это математическое представление любых данных из жизнедеятельности человека, между которыми прослеживается связь. Граф состоит из вершин и ребер, где вершины — это любой тип закономерных данных, а ребра — это линии взаимосвязей между вершинами. Граф можно встретить в математике, информатике, в физике, химии, психологии, управлении и в других сферах науках. Но в основном граф связывают с информатикой и вычислительными технологиями.
Самый простой пример графа — это построение схемы перелетов самолетов какой-либо авиакомпании. В этом случае аэропорты на карте — это вершины графа, а ребра графа — это маршруты самолетов, курсирующих между аэропортами. Взгляните на расположение файлов в компьютере — это тоже граф, где диски, папки, файлы — это вершины графа, а зависимость и вложенность папок и файлов между собой — это будут ребра графа.
Графы бывают разные. Виды графов напрямую зависят от взаимосвязей между вершинами, то есть от строения, количества и расположения ребер графа.
Что такое граф или теория графов для чайников
Теория графов — это большой раздел в дискретной математике, в котором подробно изучают характеристики различных видов графов. Именно теория графов помогает адаптировать это математическое моделирование любой информации во многие сферы жизнедеятельности человека, включая бизнес, логистику и разные науки.
Для чего вообще нужны графы? Для того чтобы визуально отразить отношение и взаимодействие между какими-то элементами в общей системе, начиная от самолетов в международном авиасообщении и заканчивая молекулами в каком-либо веществе.
Какие бывают графы
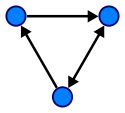
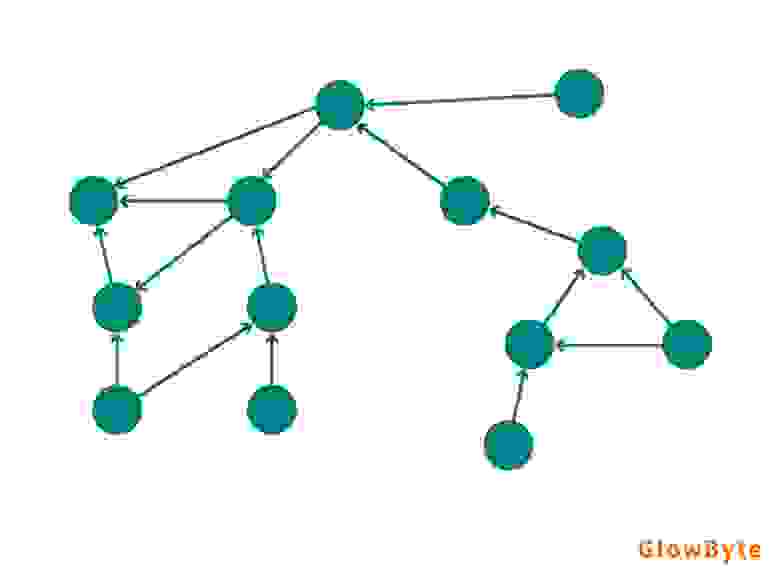
Ориентированный граф — это граф, у которого направление ребер имеет существенное значение и поэтому ребра задаются со стрелками на конце, например:
Иногда граф бывает смешанным, это когда часть ребер идет с обязательным направлением, а часть без направления. Такие графы редкие, но они есть, например:
Какими еще бывают графы
Мультиграф — это такой вид графа, когда между вершинами графа происходит несколько видов связей, то есть между двумя конкретными вершинами может быть несколько разных ребер, например:
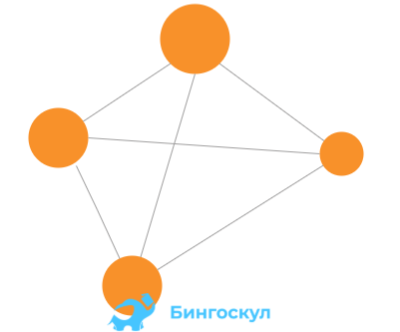
Полный граф — это такой граф, вершины которого соединены между собой всеми доступными вариантами. То есть каждая отдельная вершина соединена со всеми вершинами графа, например:
Эйлеров граф — это такой граф, у которого можно обойти все вершины, причем пройдя по каждому ребру только один раз. По своей конструкции он напоминает полный граф, о котором мы говорили чуть выше. Важная особенность — у Эйлерова графа может быть только четное количество ребер, с нечетным количеством ребер Эйлеров граф не получится. Еще такой вид графа можно определить так: любой граф, вершины которого вы сможете соединить всеми доступными ребрами, не отрывая карандаша от листочка бумаги, будет Эйлеровым графом.
Гамильтов граф — это такой граф, у которого можно обойти все вершины графа, посетив каждую из них только один раз.
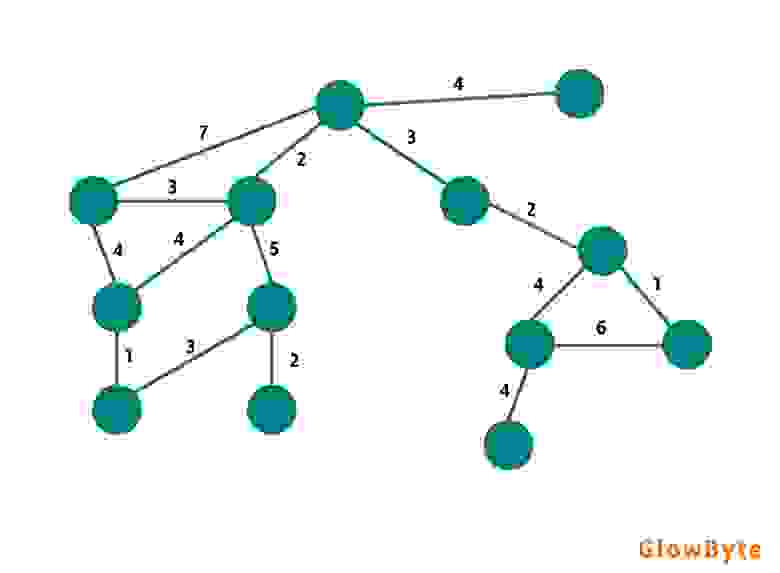
Взвешенный граф — это такой граф, у которого вершинам и/или ребрам присваивается какое-то числовое значение, это значение означает «вес» или «стоимость» ребра или вершины.
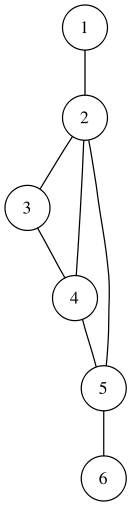
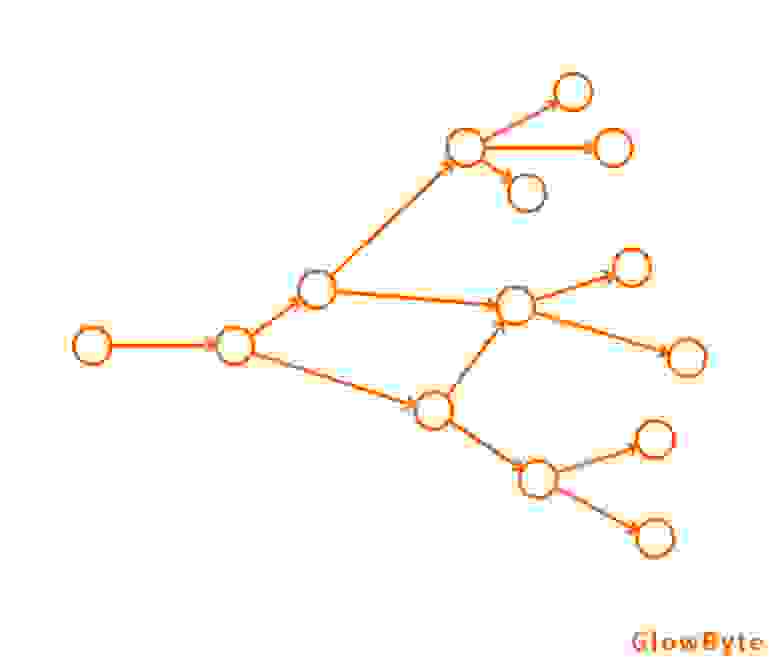
Граф-дерево — это такой вид графа, у которого все вершины связаны без циклов, а строго в иерархическом порядке. У такого графа у любых двух вершин будет только одно ребро или путь соединения. Это самый распространенный вид графа, который используется человеком вне науки. В жизни такие графы можно выделить при организации управленческой структуры в школах, организациях, структурах и государствах. Суть такого графа заключается в том, что у него есть «корень графа», то есть это та вершина, с которой начинается весь граф. У людей это может быть: директор, старший менеджер, глава ведомства, мэр, президент и т. д. Граф-дерево может выглядеть вот так:
Граф (теория графов)
В математической теории графов и информатике граф — это совокупность объектов со связями между ними.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.
V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 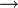
Смешанный граф
Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi 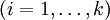
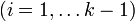
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
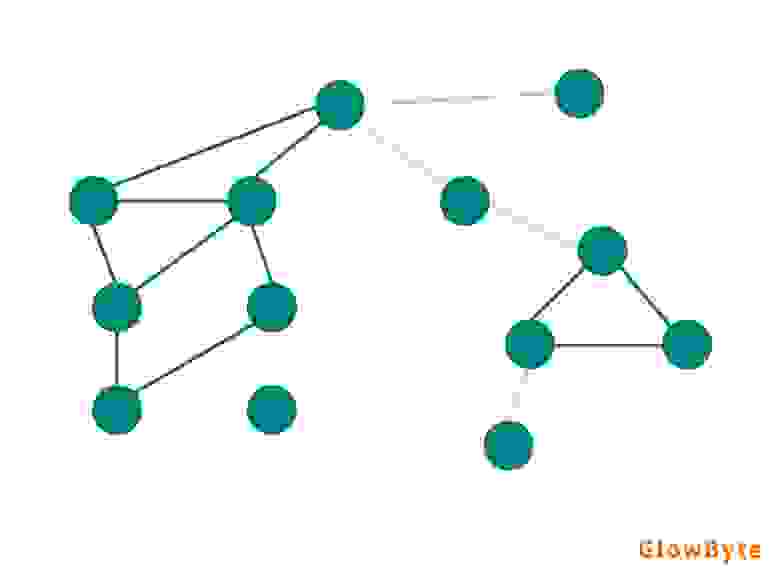
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Способы представления графа в информатике
Матрица смежности
Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти — очевидно, квадрат количества вершин.
Матрица инцидентности
Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 


Под данное выше определение не подходят некоторые другие обобщения:
Литература
См. также
Ссылки
Популярные программы для визуализации графов
Графовый анализ — обзор и области применения
Но перед этим мы вспомним основные понятия графа, поговорим о его свойствах и расскажем о семействах алгоритмов, применяемых в графовом анализе.
Что такое граф?
Граф— математический объект, который изображает отношения между сущностями. Граф состоит из вершин (объектов) и рёбер (связей). С помощью графов можно представить разныех ситуации: например, пользователей соцсети, которые находятся друг у друга в друзьях, клиентов банка, которые переводят друг другу денежные средства, географические объекты и пути между ними.
Граф называется циклическим, если в графе присутствует последовательность рёбер, которая начинается и заканчивается в одной вершине. Цикл необязательно должен включать в себя все вершины.
Графовый анализ
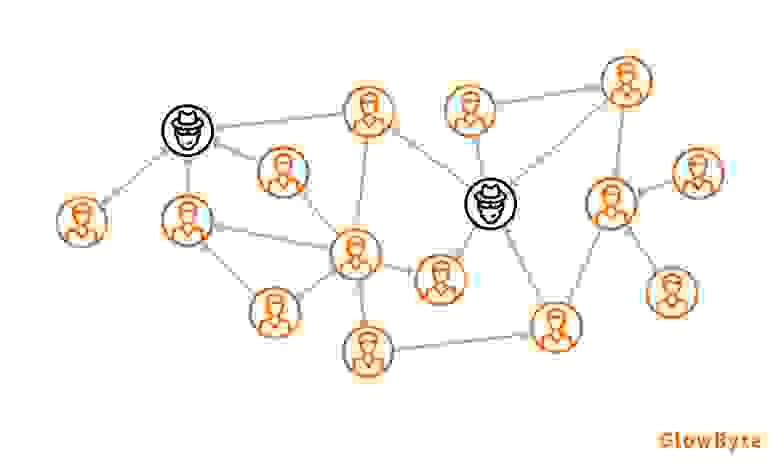
Извлекать из графов полезную информацию позволяют графовые алгоритмы, которые можно условно поделить на несколько семейств. Рассмотрим эти семейства на примере социальной сети:
Алгоритмы центральности (centrality algorithms) поможет выявить лидеров мнений и влиятельных людей в сообществах. Под центральностью мы подразумеваем некоторую меру значимости вершины или ребра.Алгоритмы центральности и сообществ можно применять для создания новых предикторов в ML-pipeline.
Предсказание связей (link prediction) оценивает вероятность наличия связи между двумя отдельными людьми в том случае, если её не существует на графе. Связи, подобранные таким образом, могут помочь в рекомендации друзей.
Алгоритмы сходства (similarity algorithms) пригодятся, чтобы найти похожие группы людей. Это может быть полезно, чтобы собрать аудиторию для рекламы по принципу lookalike или выявить поддельные учетные записи, основываясь на свойствах их окружения.
Takeaway: Графовый анализ эффективен, когда мы рассматриваем объекты в контексте связей с другими объектами.
Работа с графами
Взаимодействие с графами отличается от взаимодействия с привычными таблицами. Для этого существуют специальные программные решения, которые перечислим ниже.
Графовые базы данных
Графовые базы данных традиционно относят к NoSQL-категории. Рассмотрим их особенности:
По сравнению с реляционными и документарными БД, графовые базы позволяют создавать гибкую структуру, в которую можно вносить любые изменения, не ломая её общую архитектуру.
Для общения с графовыми СУБД существуют отдельные языки запросов, например, Cypher (Neo4j) и SPARQL.
Графовые СУБД выигрывают у реляционных в скорости в тех случаях, когда мы работаем со связями и перемещаемся по графу. Это обусловлено тем, что каждая вершина графа вместе со своими связями хранится в оперативной памяти, и не используется JOIN.
Другие инструменты работы с графами
Помимо графовых СУБД, для работы с графами существуют специальные программные библиотеки (например, для Python написаны популярные библиотеки NetworkX и igraph). Также при необходимости логику графовых вычислений можно частично реализовать и в реляционных базах данных.
В каких бизнес-областях применяются графы?
Выше мы упоминали некоторые идеи для применения графового анализа. Эти методы не обязательно привязаны к узкому набору отраслей. Ниже рассмотрим способы использования графов и приведем примеры бизнес-областей, в которых они применимы.
Мы условно разделили бизнес кейсы на три группы:
Алгоритмы на графах
С помощью графов возможно придать новую интуитивно понятную структуру привычным задачам. Притом графовое представление не только отлично подходит для математических вычислений, но и поощряет пространственное мышление. Посмотрим, как графы позволяют по-новому взглянуть на решение некоторых задач.
Рекомендательные системы
Рекомендательные системы обычно включают в себя контент-ориентированные методы (сходство продуктов между собой) или коллаборативную фильтрацию (сходство предпочтений похожих пользователей).
Рекомендации возможно делать и на графах. Например, в соцсети “Одноклассники” на графах основан подбор релевантных сообществ для пользователей:
В качестве вершин берутся сообщества, а для ребер выбирается показатель схожести этих сообществ (например, доля общих участников). Таким образом, сильнее оказываются связаны те группы, которые разделяют больше участников, а не связанные между собой группы оказываются отделены друг от друга и на графе.
Чтобы определить сообщества, которые можно рекомендовать отдельно взятому пользователю, запускается многократный случайный обход графа с началом в одном из сообществ, в которых этот пользователь уже состоит.
Те вершины, на которых останавливаются случайные обходы, считаются кандидатами для рекомендации.
Графовый подход помог “Одноклассникам” увеличить релевантность своих рекомендаций и повысить количество вступлений в группы на 30%, а благодаря скорости работы графов количество генерируемых рекомендаций удалось увеличить в 4 раза.
Портрет клиента 360 градусов
Чем лучше компания знает потребности своей аудитории, тем выше качество её сервиса, тем лучше она удерживает своих пользователей и большую прибыль генерирует.
Пользуясь табличными данными, можно анализировать статистические показатели клиентов и групп, обобщать клиентов с помощью кластеризации.
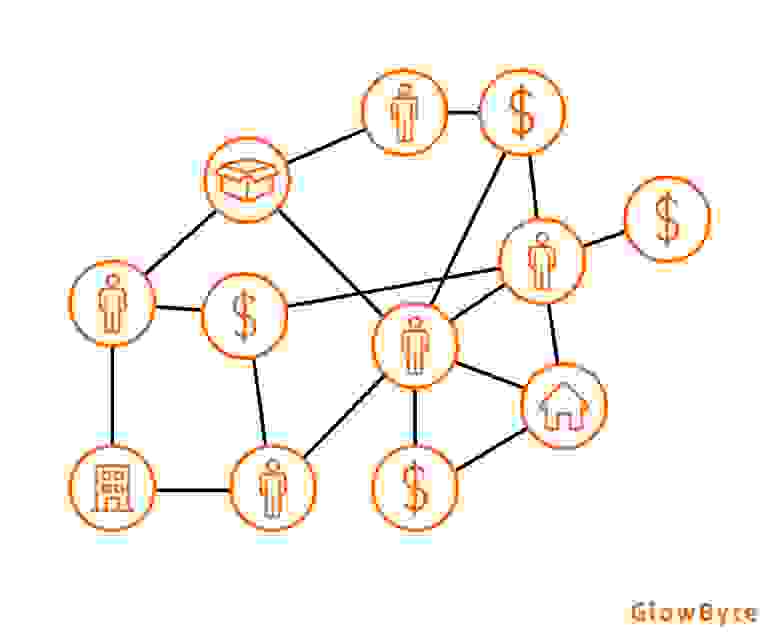
Если представить клиентов компании и их взаимодействия с продуктом и между собой в виде графа, получится визуализация, которая будет полезна для всестороннего изучения клиентов и поиска новых идей:
Применяя алгоритмы центральности, можно находить хорошо продаваемые товары или услуги.
Чтобы понять, какие продукты интересны клиенту, можно прогнозировать вероятность связей между клиентом и различными продуктами, а также делать рекомендации и решать задачу Next-Best-Action.
Если предоставить службе поддержки возможность видеть историю действий пользователя в виде графа в реальном времени, то будет проще выявить проблему, с которой столкнулся пользователь, и оперативно найти решение.
Если необходимо прогнозировать отток, то можно изучить точки соприкосновения/сходства у клиентов, которые перестали пользоваться услугами компании, а затем найти тех, кто находится в зоне риска, и постараться их удержать.
Оптимизация маршрутов (Vehicle Route Problem)
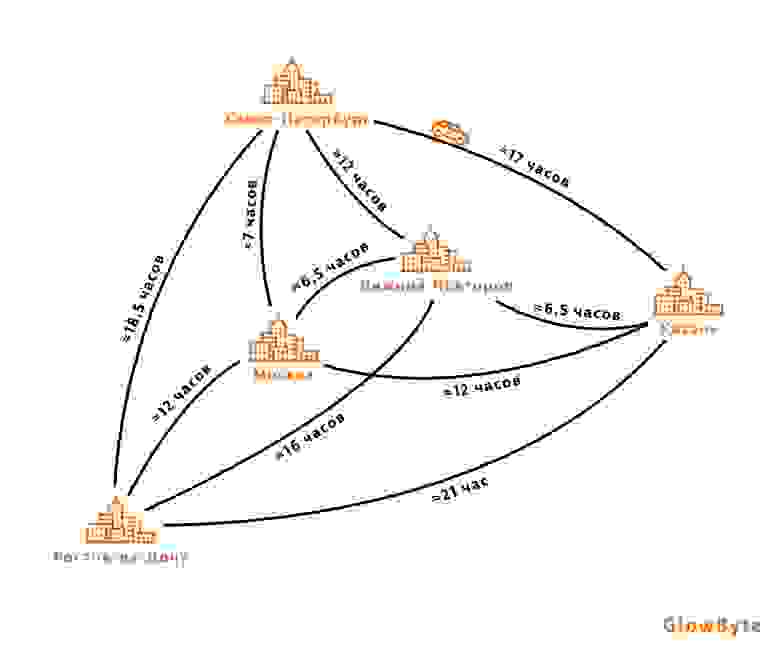
Задача оптимизации маршрутов уже имеет графовую природу: чтобы построить маршрут, можно представить пункты назначения в виде вершин графа, а рёбрами станет расчётное время, за которое водитель перемещается между пунктами. Таким образом, с помощью алгоритмов поиска путей возможно найти оптимальные варианты маршрутов.
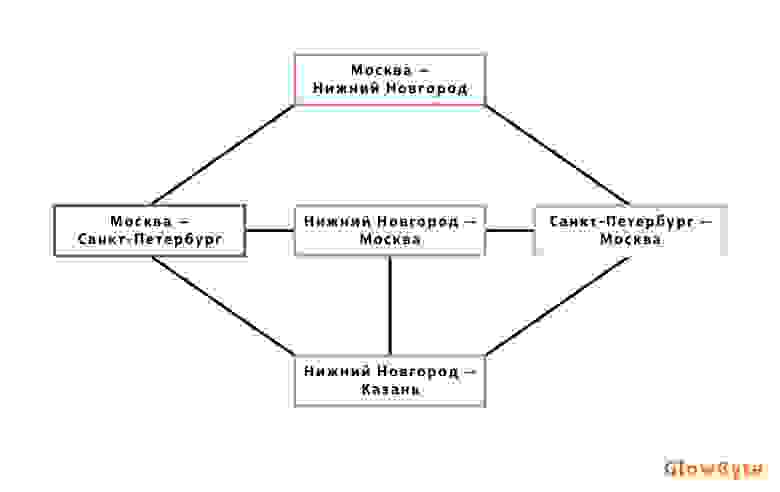
Есть и более сложный пример применения графов: допустим, у компании-перевозчика есть два заказа на одно и то же время, но в разных местах. Один курьер не успеет доставить оба заказа вовремя, даже если маршрут будет построен оптимальным образом. Было бы удобно строить маршрут сразу только из тех заказов, которые сочетаются между собой. Для этого:
Строится граф, вершинами которого будут все возможные перегоны между нашими заказами, а ребрами соединяются те перегоны, которые невозможно включить в один маршрут.
В таком графе останутся наборы не связанных рёбрами перегонов (т.е. совместимых по времени), и, используя алгоритм поиска максимальных независимых множеств, можно выделить не противоречащие друг другу отрезки пути и сформировать из них оптимальный маршрут
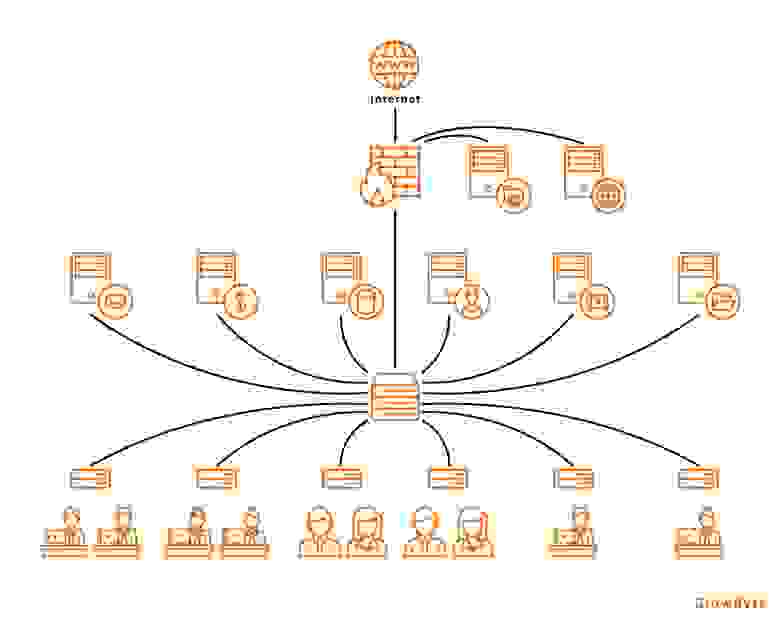
IT-инфраструктура (Predictive Maintenance and Quality)
Предиктивный анализ оказывается полезен, когда необходимо поддерживать сетевую инфраструктуру в рабочем состоянии, предупреждать отказы оборудования и повышать производительность своих сервисов.
Эти задачи решают, используя логи производительности. В них можно кластеризовать метрики производительности сети (например, пропускную способность, задержку, потерю пакетов), условно разделив работу сети на периоды высокой и низкой производительности. Изучая такие кластеры, можно понять, от каких факторов зависит качество работы сети, и использовать эту информацию для её оптимизации.
Также можно рассмотреть логи как временные ряды и искать в них аномальные значения или паттерны, которые влекут за собой отказ элементов сети.
Сетевые инфраструктуры уже являются готовыми графами, и их возможно представить в виде виртуальных графов.
Применяя алгоритмы центральности и поиска сообществ, возможно выявить такие маршруты в инфраструктуре, которые подвержены наибольшей нагрузке и требуют укрепления за счет создания резервных маршрутов.
При выявлении слабых мест в инфраструктуре также обнаруживаются те части системы, которые выйдут из строя в случае отказа сетевого оборудования.
Графы хакерских атак
Чтобы эффективно защищать цифровые активы, важно постоянно проверять сетевую безопасность на предмет уязвимости к хакерским атакам и иметь представление о том, какие ее элементы наиболее подвержены риску проникновения.
Графы атак являются направленными и представляют собой состояния сети в роли вершин и уязвимости, изменяющие эти состояния, в виде дуг.
Анализ путей и центральности позволяет распознать уязвимости и найти среди них те, которые сопряжены с наибольшим риском.
Автоматическое построение таких графов ускоряет процесс поиска слабых мест и позволяет исключить влияние человеческого фактора.
Графовые признаки для задач машинного обучения
Благодаря графовым алгоритмам у нас появляется возможность дополнять данные о наших объектах такими необычными метриками, как центральность или сходство с интересующим нас объектом. Эти признаки хороши, когда мы имеем дело с клиентами, чьё поведение зачастую сложно оценить на основе только лишь табличных данных.
Кредитный скоринг
Для кредитных организаций вопрос оценки надежности клиентов всегда актуален. И чем точнее будет эта оценка, тем в более выгодном положении будет компания и тем меньшими средствами она рискует при выдаче кредитов.
Для оценки заемщиков обычно используются всевозможные их характеристики: финансовые показатели, данные о собственности, ранее выданных кредитах итд. Эти данные сопоставляют со статистикой дефолтов, чтобы экспертно или с помощью машинного обучения выявить в них закономерности, характерные для дефолта.
Таким образом компания может заблаговременно оценить, какие условия предлагать своим клиентам, а кому и вовсе стоит отказать.
Газпромбанк (источник) использует графы для скоринга потенциальных и уже существующих заемщиков среди предприятий малого и среднего бизнеса:
В качестве вершин берутся юридические лица с различными атрибутами: например, как давно основана компания, были ли сообщения о банкротстве, итд.
Ребра между вершинами могут содержать разные виды связей, такие, как общие руководители, дочерние предприятия или наличие транзакций между компаниями. Транзакции описываются в свободной форме, и для их интерпретации и группировки по смыслу используются методы NLP.
Построенный граф применяется для создания новых признаков компаний, основанных на расстоянии между вершинами, центральности и статистических расчетах. Эти метрики могут давать прирост к качеству скоринга по сравнению с моделями, не использующими графы.
Обнаружение мошенничества (anti-fraud):
Выявление мошенничества актуально, в первую очередь, в банках: часто возникают случаи, когда карты клиентов используются злоумышленниками. Помимо этого, мошенники в компаниях могут использовать блага компании в своих целях, например, продавать продукт по сниженной цене, не регистрируя транзакцию, и класть деньги себе в карман, прикладывать свою карту с кэшбэком итд.
Традиционная реализация антифрода подразумевает в основном количественные показатели и временные ряды: число операций по карте за период, сумму разовой покупки. Модель выучивает типичное поведение клиента и воспринимает отклонение от него как повод заблокировать операцию.
Если бизнес ранее сталкивался с мошенничеством, поиском сообществ можно найти на графе группы элементов и связей, в том числе тех, в которых это мошенничество встречалось. Алгоритмы сходства, в свою очередь, позволяют сравнить любое сообщество с мошенническим и использовать силу этого сходства как ещё один предиктор для классификации транзакций или клиентов.
Может оказаться, что клиент связан с мошенником не напрямую, а через нескольких других людей, что затрудняет ручной анализ таких кейсов. Алгоритмы предсказания связей и поиска пути могут раскрыть такие неочевидные взаимодействия и указать на возможных посредников.
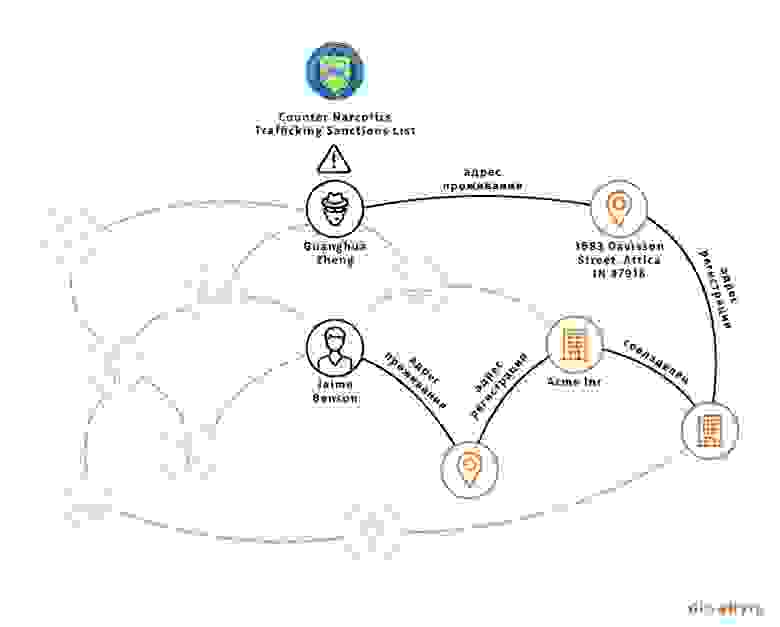
Противодействие отмыванию денег (Anti-Money Laundering) (алгоритмы)
Аналогично ситуации с антифродом, графовые методы помогают взять клиента со всеми его связями (будь то транзакции, совместные счета с другими клиентами, адреса или даже банкомат, к которому подходили два разных человека) и оценить схожесть полученной сети с уже найденными схемами отмывания денег, чтобы получить новые признаки и с их помощью усилить способность модели выявлять паттерны поведения клиентов, характерные для отмывания денег.
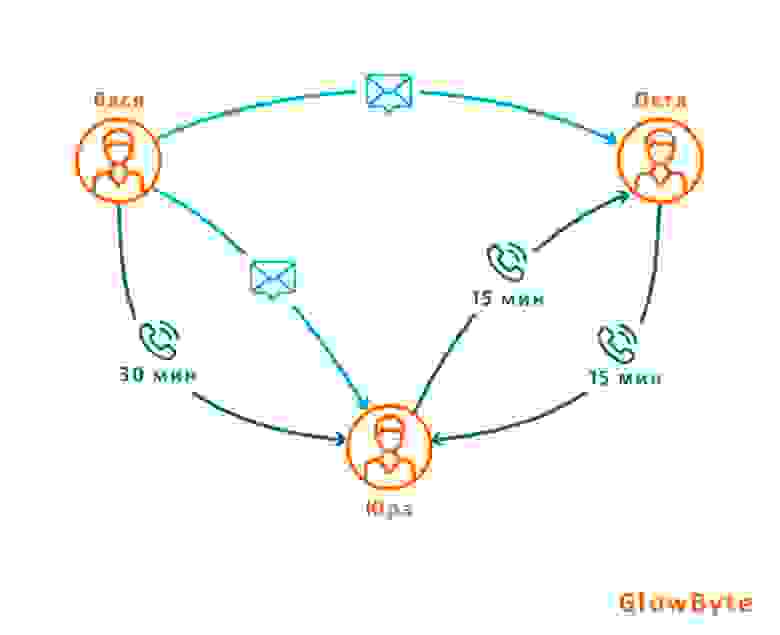
Прогноз оттока на примере телеком-оператора (Churn prediction)
Привлечение новых клиентов, как правило, требует больших усилий и затрат, чем удержание существующих. К тому же, число не подключенных ни к одному оператору людей на Земле стремительно сокращается, приток новых клиентов постепенно замедляется: как следствие возникает конкуренция компаний за пользователей.
Традиционно, пользователь представлен в виде отдельной единицы, к которой относятся персональные данные, тарифы, детализация звонков, сообщений итп. На основе этих признаков оценивается вероятность ухода нашего клиента.
Предположим ситуацию: абонент часто общается с людьми, которые в какой-то момент расторгают договор с оператором. Можно сделать допущение, что этот абонент с некоторой вероятностью последует их примеру и тоже уйдёт. В таком случае, для каждого клиента можно посчитать число ушедших ближайших контактов и использовать этот признак вместе с остальными табличными характеристиками клиента.
Хранение и структурирование информации
Многие процессы и даже те из них, в которых на первый взгляд нет готовой графовой структуры, удобно представлять в виде графов. Таким образом становятся возможными ранее недоступные способы решения задач. Используя мощный потенциал графов для работы со связями, можно решать сложные задачи в самых разных областях.
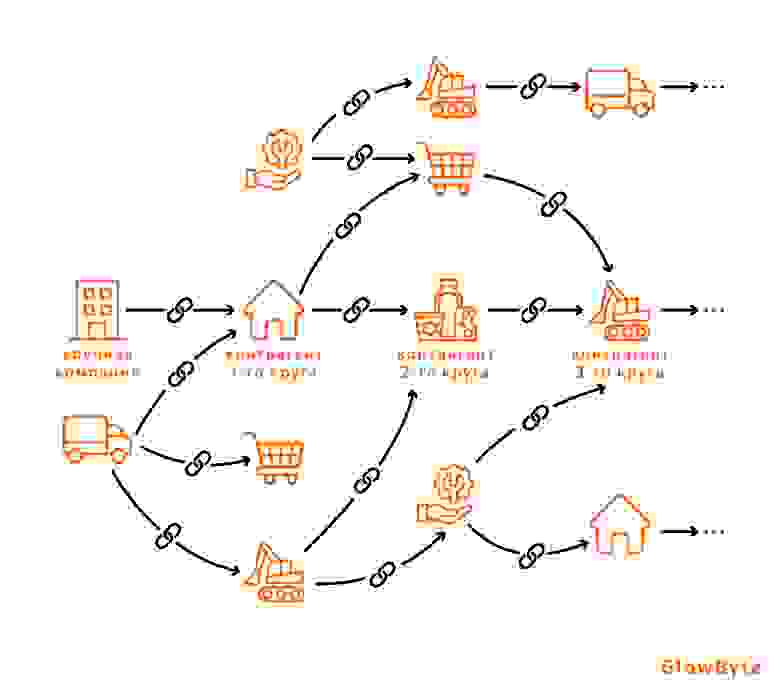
Происхождение данных (Data Lineage)
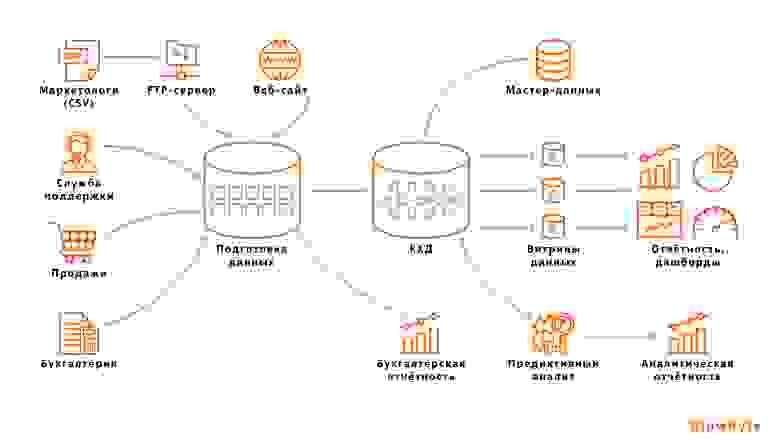
Многие компании для сбора информации вынуждены обращаться к разнообразным внешним источникам. Например, банки для построения своих моделей используют данные о транзакциях, отчетностях и кредитных историях своих клиентов, а также социально-демографические признаки, если речь идёт о физических лицах. Такое многообразие информации подразумевает наличие большого числа не связанных между собой источников и систем, в которых сложно ориентироваться. К тому же, подобная структура данных затрудняет централизованное хранение данных.
Data Lineage можно хранить в базе данных в виде направленного графа. В качестве вершин берутся источники данных, витрины и всё, что находится между ними, а дугами обозначается та информация, которая перемещается из одного места в другое.
Графовая СУБД обеспечит наглядную визуализацию и высокую скорость выполнения запросов, даже если в хранилище данных будут десятки тысяч объектов.
Если сделать граф версионным, можно будет перемещаться в разные состояния хранилища и находить моменты, в которые были допущены ошибки.
Анализ ведомости материалов
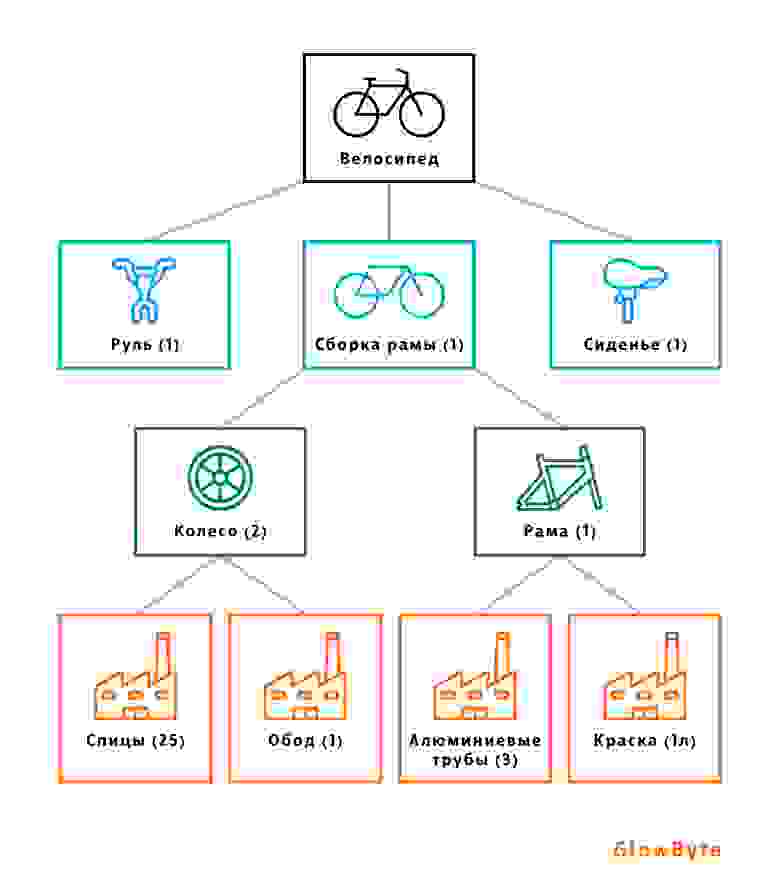
Ведомость материалов (Bill of Materials или просто BOM) — это список материалов или запчастей, необходимых для производства, сборки или ремонта конечного продукта, с указанием количества по каждому пункту. BOM используются в первую очередь для обеспечения стабильной работы производственных потоков.
Важно как можно точнее оценивать стоимость деталей, знать, для какого оборудования они нужны, прогнозировать срок их службы, чтобы производить замену, не дожидаясь поломок.
В базе данных с огромным количеством информации крайне сложно оперировать данными и отслеживать актуальное состояние техники. Например, BOM для одного танка может включать в себя миллион записей. И запчасти для него могут заказываться миллионами.
Ведомость материалов можно представить в виде графа: оборудование и запчасти станут его вершинами. Таким образом, связав готовый танк с деталями, требуемыми для его производства и обслуживания, аналитик получает наглядную структурированную информацию, а благодаря реализации этого подхода в графовой базе данных скорость работы значительно увеличивается.
В качестве вершин можно дополнительно взять военные подразделения и поставщиков: тогда с помощью алгоритмов поиска путей и запросов к базе станут возможны оперативная и точная оценка стоимости закупок, а также подбор оптимальных каналов поставки деталей.
Neo4j в описании кейса армии США отмечено, что применение графов позволило сократить время получения искомых данных с 60 часов до 7-8 часов, а поддерживать такую базу теперь могут всего 2 человека, а не 9, как раньше.
Графы знаний для построения поисковых запросов
В качестве примера, как используются графы при поиске товаров, подойдёт совместный кейс eBay и Google.Целью проекта было создание чат-бота для Ассистента Google, который умел бы искать товары на основе речевых запросов и умел бы уточнять поисковый запрос, общаясь с пользователем.
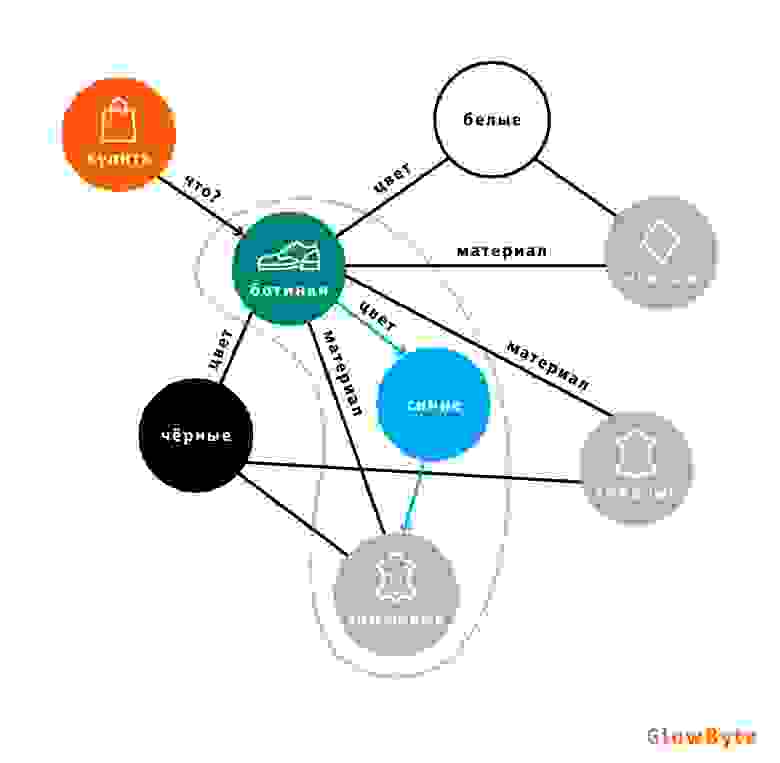
В основу поискового решения был положен граф знаний, вершины которого представляют виды товаров, их свойства и значения этих свойств. Свойства связаны с товарами, которые ими обладают.
Такой граф решает сразу две задачи:
С одной стороны, когда пользователь задаёт сложный поисковый запрос в духе “ищу палатку, чтобы съездить вместе с супругой/супругом отдохнуть на озеро Тахо”, механизмы NLP извлекают смысл сказанного, находят на графе близкие по смыслу вершины-характеристики и предлагают пользователю товары, связанные с этими вершинами.
С другой стороны, Google Ассистент может задавать пользователю уточняющие вопросы, двигаясь по графу от общих категорий к более детальным, тем самым дополняя свою информацию об искомом товаре и предлагая более релевантные товары. Благодаря быстрой обработке связей графовой СУБД Google Ассистент может взаимодействовать с человеком в реальном времени.
Заключение
Графовый анализ предлагает нам новые способы взаимодействия с привычными данными, такие как:
Визуализация связей между объектами;
Генерация новых признаков для машинного обучения;
Анализ объектов в контексте их окружения.
Для работы с графами уже существует достаточно большое число различных инструментов:
Программные библиотеки для Python и других языков.
Использование графов не ограничивается узким набором бизнес-областей. Если проявить фантазию, можно найти для графов самые неожиданные применения.
Графы вряд ли могут полностью заменить традиционные подходы к решению задач, но окажутся отличным подспорьем и при грамотном использовании помогут усовершенствовать существующие подходы к решению многих задач в аналитике данных и машинном обучении.
Больше про графы в реальных бизнес-задачах мы общаемся в нашем сообществе NoML: