Что такое горизонтальная прямая

Горизонтальная прямая

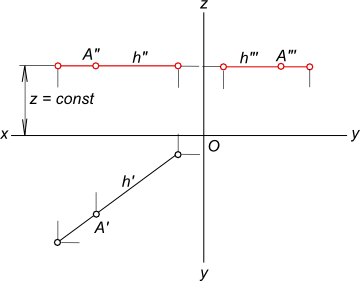
Приведенная запись означает: для множества точек A, принадлежащих прямой h, аппликата есть величина постоянная, характеризует удаление точек от горизонтальной плоскости проекций.

Горизонтальная прямая h –

Горизонтальная прямая относится к Частному случаю расположения прямой

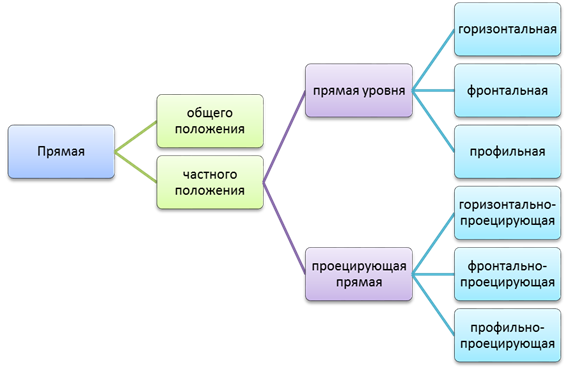
Кроме общего положения, прямая по отношению к заданной системе плоскостей проекций может занимать частное положение. Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня. Существует три вида прямых уровня: горизонтальная прямая (горизонталь), фронталь и профильная прямая.

К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня.

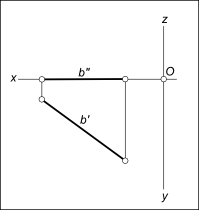
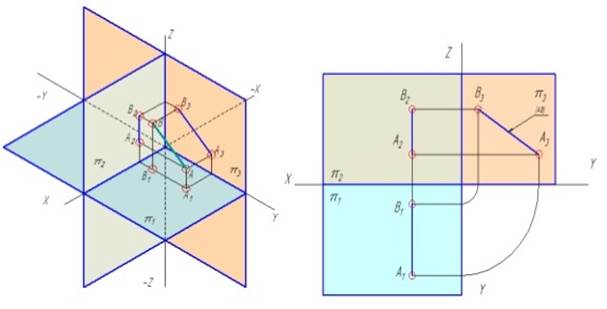
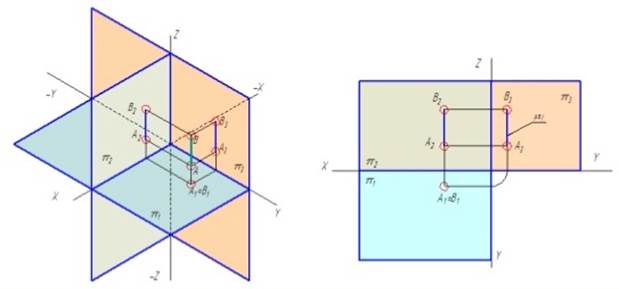
На рисунке приведена горизонтальная прямая нулевого уровня: горизонталь h располагается на горизонтальной плоскости проекций, следовательно ее фронтальные проекции находятся на оси O_x.

По расположению относительно плоскостей проекций бывают прямые частного положения: Фронтальная прямая; Профильная прямая; Проецирующие прямые.

Источник

Горизонтальная прямая

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной. На рисунках 4, 5 изображен отрезок прямой АВ║π₁.

а) горизонтальная проекция горизонтальной прямой равна длине самого отрезка (А′В′ = [AB]);

б) фронтальная проекция горизонтальной прямой параллельна оси проекций «х». Если, например, А″В″ совпадает с осью проекций х, то это соответствует положению отрезка АВ в плоскости проекций π₁;

в) угол, образованный горизонтальной проекцией прямой и осью «х», равен углу наклона этой прямой к фронтальной плоскости проекций

(А′В′; х=[AB]; π₂= o ).

Фронтальная прямая

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной. На рисунках 6, 7 изображен отрезок прямой CD║π₂.

Рис. 6 Рис. 7

Для фронтальной прямой следует отметить:

а) фронтальная проекция этой прямой равна длине самого отрезка (С″D″=[CD]);

б) горизонтальная проекция фронтальной прямой параллельна оси х (С′D′║х); Если, например, С′D′ совпадает с осью проекций х, то это соответствует положению CD в пл. π₂.

в) угол, образованный фронтальной проекцией прямой и осью х, равен углу наклона этой прямой к горизонтальной плоскости проекций

Профильная прямая

Прямая, параллельная профильной плоскости проекций, называется профильной. На рисунках 8, 9 изображен отрезок прямой EF║π₃.

Рис. 8 Рис. 9

Для профильной прямой характерно:

а) профильная проекция этой прямой равна длине самого отрезка (E″′F″′=[EF]);

б) горизонтальная и фронтальная проекции профильной прямой располагаются на одном перпендикуляре к оси проекций х;

Прямые, параллельные одной плоскости проекций, т.е. горизонтальные, фронтальные и профильные называются прямыми уровня.

Горизонтально – проецирующая прямая

Прямая, параллельная плоскостям π₂ и π₃, т.е. перпендикулярная к π₁, называется горизонтально-проецирующей. На рисунках 32,33 изображен отрезок прямой MN_┴π₁.

Рис. 10 Рис. 11

Источник

Положение прямой в пространстве

Прямая общего положения – прямая не параллельная ни одной из плоскостей проекций. Проецируется на все плоскости проекций с искажением.

Прямая уровня –это прямая параллельная одной из плоскостей проекций.

На эпюре: фронтальная и профильная проекции такой прямой параллельны горизонтальной оси. Горизонтальная проекция прямой представляет её натуральную величину.

На эпюре: Горизонтальная проекция прямой параллельна горизонтальной оси, а профильная перпендикулярна к этой же оси. Фронтальная проекция прямой представляет её натуральную величину.

На эпюре: Горизонтальная и фронтальная проекции такой прямой перпендикулярны к горизонтальной оси. Профильная проекция прямой представляет её натуральную величину.

Проецирующая – прямая, перпендикулярная к плоскости проекции.

Горизонтально-проецирующая – это прямая перпендикулярная к горизонтальной плоскости проекций.

На эпюре: на горизонтальную плоскость проекций проецируется в точку, а на две другие плоскости проекций – в прямую, перпендикулярную горизонтальной оси, при этом обе проекции равны истинной длине прямой.

Фронтально-проецирующая – прямая перпендикулярная к фронтальной плоскости проекций.

На эпюре: на фронтальную плоскость проекций проецируется в точку, а на две другие плоскости проекций – в прямые, перпендикулярные координатным осям, при этом обе проекции равны истинной длине прямой.

Профильно-проецирующая– прямая перпендикулярная к профильной плоскости проекций.

На эпюре: на профильную плоскость проекций проецируется в точку, а на две другие плоскости проекций – в прямую, параллельную горизонтальной оси, при этом обе проекции равны истинной длине прямой.

Дата добавления: 2015-09-07 ; просмотров: 2558 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

2.3. Частные положения прямой в пространстве

.

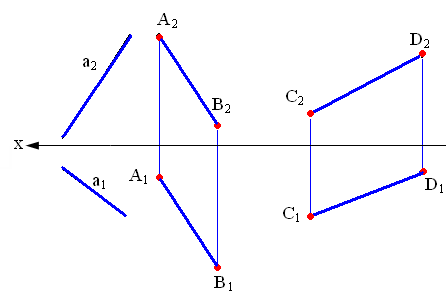
Рис. 2.1. Прямые общего положения

На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.

Прямые, параллельные плоскостям проекций.

1. Горизонтальная прямая h (рис. 2.2) – горизонталь

Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π₁.

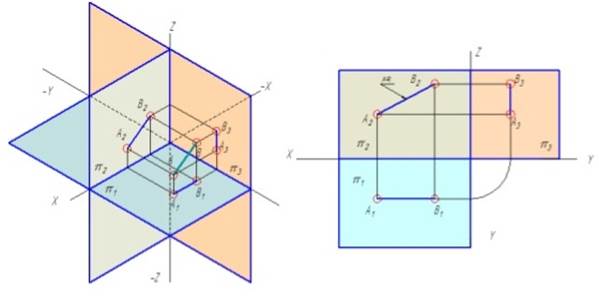
Так как все точки этой прямой равноудалены от плоскости проекций π₁ (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π₁ проецируются без искажения отрезок прямой АВ (А₁В₁=АВ) и углы наклона прямой к плоскостям проекций π₂ и π₃ (углы β 0 и γ 0 ).

2. Фронтальная прямая f (рис. 2.3) – фронталь

Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π₂. Так как все точки этой прямой равноудалены от плоскости проекций π₂ (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π₂ проецируются без искажений отрезок этой прямой CD (C₂D₂+CD) и углы наклона прямой к плоскостям проекций π₁ и π₃ (углы α 0 и γ 0 )

.

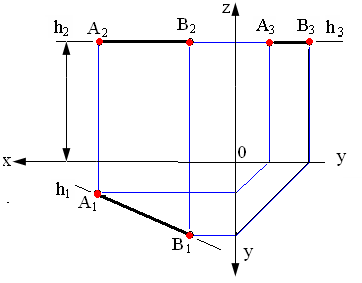
Рис. 2.2. Горизонтальная прямая

3. Профильная прямая p (рис. 2.4)

Прямые, принадлежащие плоскостям проекций

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

.

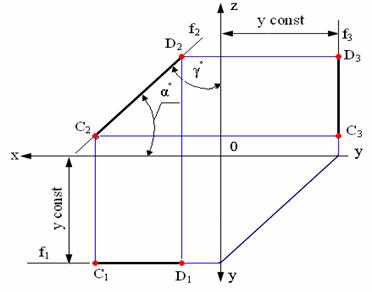
Рис. 2.3. Фронтальная прямая

.

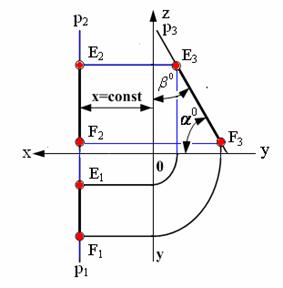
Рис. 2.4. Профильная прямая

На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).

.

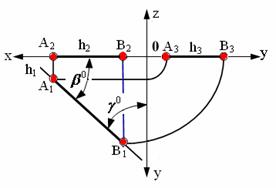
Рис. 2.5. Прямая, принадлежащая горизонтальной плоскости проекций

.

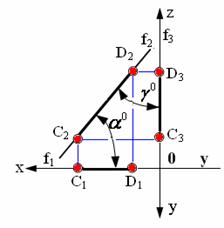
Рис. 2.6. Прямая, принадлежащая фронтальной плоскости проекций

.

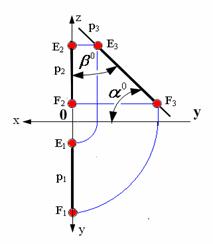
Рис. 2.7. Прямая, принадлежащая профильной плоскости проекций

Прямые, перпендикулярные плоскостям проекций.

На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций

Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π₁ в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).

Прямая, перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π₂ в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).

Прямая, перпендикулярная профильной плоскости проекций – профильно-проецирующая прямая. Эта прямая проецируется на плоскость π₃ в точку, а ее фронтальная проекция перпендикулярна оси Z.

Эти прямые являются частными случаями фронтали и горизонтали.

.

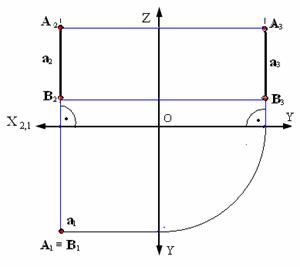
Рис. 2.8. Прямая, перпендикулярная горизонтальной плоскости проекций

.

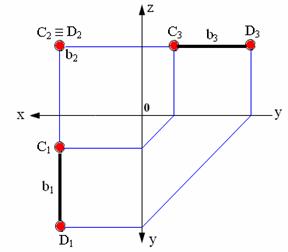
Рис. 2.9. Прямая, перпендикулярная фронтальной плоскости проекций

.

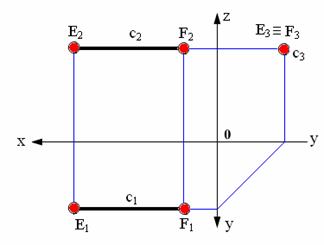
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций

Источник

Что такое горизонтальная прямая

Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).

Рисунок 18. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня . В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19). Для любой пары точек горизонтали должно быть справедливо равенство

Рисунок 19. Горизонтальная прямая

2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями ( рис.20).

Рисунок 20. Фронтальная прямая

2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).

Рисунок 21. Профильная прямая

Рисунок 22. Фронтально проецирующая прямая

4. Прямые параллельные биссекторным плоскостям (рис. 25)

5. Прямые перпендикулярные биссекторным плоскостям (рис. 25)

Источник