Что такое горизонтальная асимптота графика функции

Асимптоты графика функции

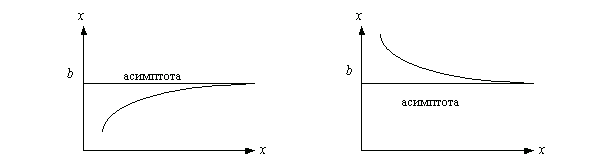
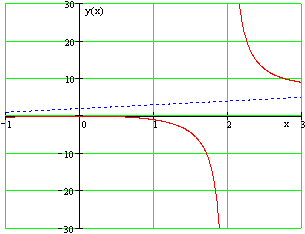
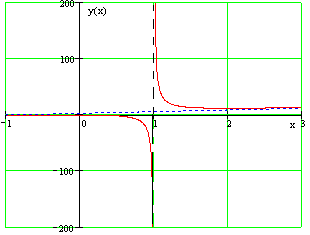
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.

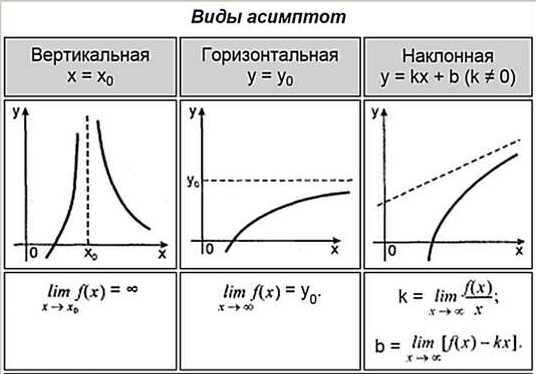
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.

Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три. и бесконечно много. У каждой функции по разному.

Вертикальные асимптоты

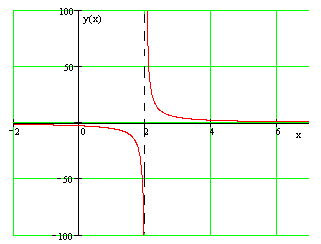
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.

Горизонтальные асимптоты

Наклонные асимптоты

Примеры решений

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Приступим к поиску наклонных асимптот.

Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты.

Нет точек разрыва, а это значит, нет вертикальных асимптот.

Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.

Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.

Источник

Асимптоты графика функций: их виды, примеры решений

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие асимптоты

Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.

Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.

Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.

Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты

Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.

Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.

Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:

Найти асимптоты графика функции самостоятельно, а затем посмотреть решения

Пример 2. Найти асимптоты графика функции .

Пример 3. Найти асимптоты графика функции

Пример 4. Найти асимптоты график функции .

Горизонтальные асимптоты

Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b), то y = b – горизонтальная асимптота кривой y = f(x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

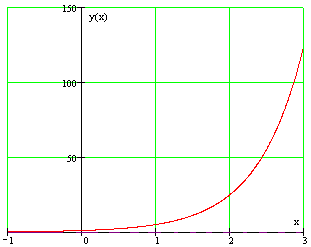
Пример 5. График функции

при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:

Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:

Наклонные асимптоты

(1)

(2)

Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.

В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.

При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.

При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример 6. Найти асимптоты графика функции

Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:

Следовательно, x = 0 – вертикальная асимптота графика данной функции.

Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:

Выясним наличие наклонной асимптоты:

Пример 7. Найти асимптоты графика функции

,

.

Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:

Пример 8. Найти асимптоты графика функции

.

Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

.

Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .

Пример 9. Найти асимптоты графика функции

.

Рассмотрим правосторонний предел при (левосторонний предел не существует):

.

Ищем наклонные асимптоты:

Пример 10. Найти асимптоты графика функции

Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :

,

.

Ищем наклонные асимптоты:

Пример 11. Найти асимптоты графика функции

.

Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие . Функция имеет две точки разрыва: , . Чтобы установить вид разрыва, найдём односторонние пределы:

Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при и при совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:

Найти асимптоты графика функции самостоятельно, а затем посмотреть решения

Пример 12. Найти асимптоты графика функции .

Пример 13. Найти асимптоты графика функции .

Источник

Асимптоты графика функции

Вы будете перенаправлены на Автор24

Достаточно часто на практике приходится иметь дело с функциями, которые определены не на всей числовой прямой, либо принимают не любые значения из множества действительных чисел.

В таких случаях при построении графиков функций получаем, что график функции не является непрерывной линией, а имеет некоторые разрывы. В результате чего становится целесообразным ввести понятие «асимптота».

Среди асимптот выделяют следующие виды:

Отметим, что асимптоты на графике функции изображаются пунктирной линией.

Готовые работы на аналогичную тему

График функции может иметь только правую либо только левую горизонтальную асимптоту.

Условия существования наклонной асимптоты определяются следующей теоремой.

Наклонная асимптота может быть левой (график приближается справа), правой (график приближается слева) или двусторонней (график приближается с обоих сторон).

Следовательно, график данной функции не имеет наклонной асимптоты.

График функции может иметь одновременно несколько асимптот, например, вертикальную и наклонную.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 02 2021

Источник

Асимптота графика функции: определение, как искать

Что такое асимптота — понятие и определение

Асимптота графика функции у=f (x) представляет собой прямую L, максимально приближающеюся к графику функции, точка которого стремится к бесконечности, то есть неограниченно удаляется от начала координат по кривой. Расстояние между этой точкой функции у=f(x) и асимптотой L стремится к нулю.

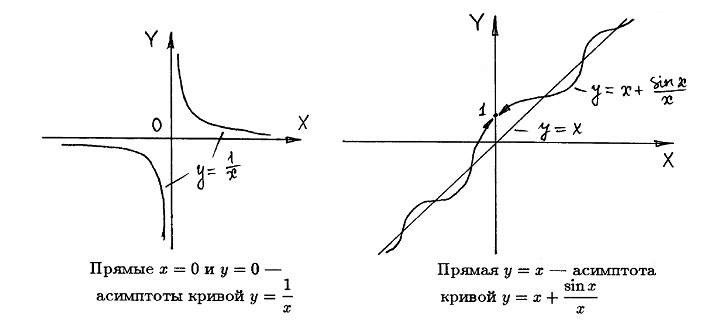
На рисунке приведены примеры асимптот графиков функций.

На рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон

Асимптоты графика функции, основные виды

Асимптоты делятся на три вида: вертикальные, наклонные и горизонтальные.

У разных функции в наличии может быть различное количество асимптот:

Приведем пример нахождения асимптот гиперболы.

Гипербола — геометрическое место расположения точек, от которых абсолютная величина разности растояний до двух фокусов (заданных точек), является постоянной и меньшей, чем расстояние между самими фокусами.

Это действительно, так как:

Следовательно, если абсцисса х неограниченно возрастает, то график гиперболы и ее асимптота неограниченно сближаются.

Расположение асимптот гиперболы соответствует диагоналям прямоугольника, стороны которого параллельны оси Ох и оси Оу, а центром служит начало координат.

Пример

Необходимо составить уравнение гиперболы, если следующие уравнения задают ее асимптоты:

Решение

Применим формулу \(y=\frac bax\) и получим:

Подставим координаты точки М в общую формулу уравнения гиперболы:

Получим систему уравнений. Чтобы получить уравнение данной гиперболы, необходимо вычислить полученную систему уравнений.

Вертикальные асимптоты

Если хотя бы один из пределов \(\lim_f(x)\) или \(\lim_f(x)\) является равным +∞ или —∞, то вертикальной асимптотой графика функции у=f(x) будет являться прямая х=с.

Примеры вертикальных асимптот:

Пример 1

Необходимо определить вертикальную асимптоту функции \(\lim_a(x)=0.\)

Решение

то x=0 — вертикальная асимптота.

Пример 2

Ось ординат является вертикальной асимптотой, так как

Наклонные асимптоты

Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.

Если k=0, то наклонная асимптота превращается в горизонтальную.

Применение правила Лопиталя

Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:

Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:

Производная может применяться многократно для получения константы в числителе или знаменателе.

Пример 1

Прямая у=х — наклонная асимптота графика данной функции.

Пример 2

Рассмотрим два варианта:

То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.

То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.

Горизонтальные асимптоты

Прямая y=b является горизонтальной асимптотой для графика функции y=f(x), если

Пример 1

Имеется функция: \(y=4+\frac1x.\)

поэтому y=4 — горизонтальная асимптота данной функции.

Пример 2

Значит, у=1 — горизонтальная асимптота графика функции.

Пример 3

Источник

Асимптоты

Вертикальная асимптота.

Если выполнено хотя бы одно из условий
$$
\lim_-0>f(x)=\infty,\qquad\lim_+0>f(x)=\infty,\nonumber
$$
то прямую \(x=x_<0>\) называют вертикальной асимптотой графика функции \(y=f(x)\).

Например, прямая \(x=0\) — вертикальная асимптота графиков функций \(y=\displaystyle \frac<1>\), \(y=\operatornamex^2\), \(y=\displaystyle \frac<1>>\), \(y=\operatornamex\), прямая \(x=-1\) — вертикальная асимптота графика функции \(y=\displaystyle \frac<3-2x>\), прямые \(x=\displaystyle \frac<\pi> <2>+\pi k\ (k\in \mathbb)\) — вертикальные асимптоты графика функции \(y=\operatornamex\).

Функции и их асимптоты

Асимптота	Функция	График функции
\(x=0\)	\(y=\displaystyle \frac<1>\)
	\(y=\operatornamex^2\)
	\(y=\displaystyle \frac<1>>\)
	\(y=\operatornamex\)
\(x=-1\)	\(y=\displaystyle \frac<3-2x>\)

Асимптота (невертикальная асимптота).

Прямую
$$
y=kx+b\nonumber
$$
называют асимптотой (невертикальной асимптотой) графика функции \(y=f(x)\) при \( x\rightarrow+\infty\), если
$$
\lim_(f(x)-(kx+b))=0.\label
$$
Если \(k\neq 0\), то асимптоту называют наклонной, а если \(k=0\), то асимптоту \(y=b\) называют горизонтальной.

Аналогично вводится понятие асимптоты при \(x\rightarrow-\infty\).

Функции и их асимптоты

Асимптота	Функция	График функции
\(y=1\)	\(y=e^<1>\)
	\(y=\operatorname	x\)
	\(y=\operatornamex\)
\(y=\displaystyle \frac<\pi><2>\)	\(y=\operatornamex\)
\(y=\pi\)	\(y=\operatornamex\)

Найти асимптоту при \(x\rightarrow+\infty\) и \(x\rightarrow-\infty\) графика функции:

Для того, чтобы прямая \(y=kx+b\) была асимптотой графика функции \(y=f(x)\) при \( x\rightarrow+\infty\), необходимо и достаточно, чтобы существовали конечные пределы
$$
\lim_\frac=k,\label
$$
$$
\displaystyle \lim_(f(x)-kx)=b.\label
$$

\(\circ\) Необходимость. Если прямая \(y=kx+b\) — асимптота графика функции \(y=f(x)\) при \(x\rightarrow+\infty\), то выполняется условие \eqref или равносильное ему условие
$$
f(x)=kx+b+\alpha(x),\quad \alpha(x)\rightarrow 0 \quad при \quad x\rightarrow +\infty.\label
$$
Разделив обе части равенства \eqref на \(x\), получим
$$
\frac=k+\frac+\frac<\alpha(x)>,\nonumber
$$
откуда следует, что существует предел \eqref.

Из равенства \eqref получаем
$$
f(x)-kx=b++\alpha(x),\ где \ \alpha(x)\rightarrow 0 \ при \ x\rightarrow+\infty,\nonumber
$$
откуда следует, что существует предел \eqref.

Для случая горизонтальной асимптоты данная теорема формулируется в следующем виде: для того, чтобы прямая \(y=b\) была асимптотой графика функции \(y=f(x)\) при \(x\rightarrow+\infty\), необходимо и достаточно, чтобы \(\displaystyle \lim_f(x)=b\).

Источник