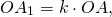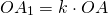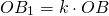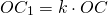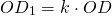Что такое гомотетия в геометрии 9 класс
Гомотетия
Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу
где k — постоянное, отличное от нуля число, O — фиксированная точка.
Точка O называется центром гомотетии, число k — коэффициентом гомотетии.
гомотетия с коэффициентом k>0
Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:
и соединить вершины A1, B1, C1и D1 отрезками.
При k
и соединить вершины A1, B1, C1 отрезками.
При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.
Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.
Свойства преобразования гомотетии
1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.
2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).
Стороны гомотетичных фигур пропорциональны. а углы — равны.
Что такое гомотетия в геометрии 9 класс
Документальные учебные фильмы. Серия «Геометрия».
Выберем ортонормированный репер (О, Е1, E2) так, чтобы точка О совпала с центром гомотетии. Если М (х, у) —произвольная точка плоскости, а точка M′ (х’, у’) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии:
. (3)
Рассмотрим простейшие свойства гомотетии.
1) Гомотетия с коэффициентом переводит прямую, не проходящую через центр гомотетии, в параллельную ей прямую, а прямую, проходящую через центр гомотетии, — в себя.
2) Гомотетия сохраняет простое отношение трех точек.
Из этих свойств следует, что гомотетия переводит отрезок в отрезок, луч в луч и полуплоскость в полуплоскость.
3) Гомотетия переводит угол в равный ему угол.
□ Пусть ВАС — данный угол, а В′ А′ С’ — образы точек В, А и С. По формуле (2) получаем:
Отсюда следует, что
4) Гомотетия сохраняет ориентацию плоскости.
Таким образом, если М (х, у) — произвольная точка плоскости, а М'(х′, у’) — ее образ в преобразовании то
где =1, если — преобразование подобия первого рода, и = — 1, если — преобразование подобия второго рода. Используя формулы (7), докажем теорему.
Теорема 2. Любое преобразование подобия, отличное от движения, имеет одну и только одну неподвижную точку.
□ Пусть равенства (7) — аналитическое выражение данного преобразования подобия. Точка М (х, у) является неподвижной точкой этого преобразования тогда и только тогда, когда
Итак, существует шесть типов преобразования подобия, которые приведены в следующей таблице:
Это отображение называется гомотетией с центром Мо и коэффициентом m. Для двух точек M1 и М2 и их образов и из формулы (1) получаем:
Отсюда и следует сформулированное выше утверждение.
Теорема 1, сформулированная и доказанная (см. выше), полностью переносится на пространство, т. е. любое преобразование подобия пространства с коэффициентом является произведением гомотетии с тем же коэффициентом и произвольным центром на некоторое движение. Отсюда следует, что подобие пространства переводит плоскость (прямую) в плоскость (прямую), параллельные плоскости (прямые) —в параллельные плоскости (прямые). Подобие сохраняет простое отношение трех точек, поэтому оно переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость, полупространство — в полупространство. Подобие переводит угол в равный ему угол, взаимно перпендикулярные прямые (плоскости) — во взаимно перпендикулярные прямые (плоскости).
Точно так же, как и на плоскости, можно доказать, что любое преобразование подобия либо сохраняет ориентацию пространства, либо меняет ее. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода. Таким образом, гомотетия с положительным коэффициентом является преобразованием подобия первого рода, а гомотетия с отрицательным коэффициентом (в частности, центральная симметрия, ) — преобразованием подобия второго рода.
Презентация по математике на тему «Гомотетия»
Описание презентации по отдельным слайдам:
ГОМОТЕТИЯ Работу выполнили: Соловьёва Алёна и Киселёва Яна, ученицы 11 «М» класса МОУ СОШ №32 Руководитель: Стаханова П.А., учитель математики МОУ СОШ №32 Исследовательская работа
Цель работы: исследование гомотетии и её свойств, а также применение гомотетии при решении задач. Методы исследования: Изучение теории Доказательства некоторых свойств гомотетии Установление связи между гомотетией и решением задач Выполнение практической части
Данная тема является дополнением и углублением изученных в курсе геометрии свойств гомотетии. 2. Применение опыта решения планиметрических задач с использованием гомотетии помогает повысить уровень пространственного воображения и уровень логической культуры. 3. Изучение данной темы поможет более глубоко подготовиться к вступительным экзаменам и успешному участию в математических конкурсах и олимпиадах. Актуальность
Свойства гомотетии 1. Отрезок, соединяющий две произвольные точки плоскости, не лежащие на одной прямой с центром гомотетии, и отрезок, соединяющий образы этих точек, параллельны.
2. Всякая прямая, не проходящая через центр гомотетии, преобразуется в параллельную ей прямую.
3. При гомотетии отрезок преобразуется в отрезок.
4. При гомотетии угол преобразуется в равный ему угол.
5. При гомотетии многоугольник преобразуется в подобный ему многоугольник.
Гомотетичные окружности Всякая гомотетия отображает окружность на окружность, так как при гомотетии все расстояния умножаются на одно и то же число – модуль коэффициента гомотетии.
Задача №1 Докажите, что точки, симметричные произвольной точке относительно середин сторон квадрата, являются вершинами некоторого квадрата.
Задача №2 Объём треугольной пирамиды 1. Найдите объём пирамиды с вершинами в точках пересечения медиан данной пирамиды.
Доказательство: гомотетичен при 2. Соответственные стороны этих треугольников параллельны
1. Анализ теоретического материала по гомотетии позволил узнать свойства и область применения гомотетии, а также помог повысить наш уровень пространственного воображения и уровень логической культуры. 2. Решение практических задач показало, что многие задачи, даже очень сложные, можно решить с помощью гомотетии, сэкономив при этом и время, и силы. 3. Мы узнали много нового и интересного, работая над данной темой. Это действительно занимательно и увлекательно. Надеемся, что эта тема пригодится нам в будущем при участии в математических олимпиадах и при ЕГЭ
«Обладая литературой более обширной, чем алгебра и арифметика вместе взятые, и, по крайней мере, столь же обширной, как анализ, геометрия в большей степени чем любой другой раздел математики, является богатейшей сокровищницей интереснейших, но полузабытых вещей, которыми спешащее поколение не имеет времени насладиться». Е. Т. Белл. Заключение
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-455932
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В Хабаровске родители смогут заходить в школы и детсады только по QR-коду
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Чем заняться с детьми в новогодние праздники в Москве
Время чтения: 4 минуты
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Свойства, типы и примеры гомотетии
homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.
homotecia
Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..
Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:
Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..
С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..
свойства
Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:
— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.
— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.
— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:
С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:
— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.
— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).
— Если k> 1, размер преобразованного рисунка будет больше размера исходного.
— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:
Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.
Презентация была опубликована 8 лет назад пользователемВладислава Муравцева
Похожие презентации
Презентация 9 класса на тему: «Гомотетия Подготовила: Карсанова Саида ученица 9 Б класса МОУ СОШ 5.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Гомотетия Подготовила: Карсанова Саида ученица 9 Б класса МОУ СОШ 5
0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″ title=»Гомотетия с коэффициентом k > 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″ > 2 Гомотетия с коэффициентом k > 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″> 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″> 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″ title=»Гомотетия с коэффициентом k > 0 Точки A и А 1 гомотетичны относительно точки О, если:Точки A и А 1 гомотетичны относительно точки О, если: 1) А 1 лежит на луче ОА 2) ОА 1 = k ОА. О А А1А1 3АО k = 3k = 3″>
3 Построение гомотетии с коэффициентом k = 1/4 О В В1В1 ОВ 1 4
4 y2y2 y1y1 x1x1 x2x2 kx 1 kx 2 ky 2 ky 1 x y Построение гомотетии.
5 Из определения гомотетии следует, что при k = 1 гомотетия является тождественным преобразованием.Из определения гомотетии следует, что при k = 1 гомотетия является тождественным преобразованием. При k = –1 гомотетия становится центральной симметрией.При k = –1 гомотетия становится центральной симметрией. Две гомотетии с центром в O и коэффициентами k и 1/k являются взаимно обратными. Это означает, что если одна из них переводит точку A в точку A 1, то другая переводит A 1 в A.Две гомотетии с центром в O и коэффициентами k и 1/k являются взаимно обратными. Это означает, что если одна из них переводит точку A в точку A 1, то другая переводит A 1 в A.
6 Свойства гомотетии с коэффициентом k. Прямая переходит в параллельную прямую.Прямая переходит в параллельную прямую. Угол переходит в равный ему угол.Угол переходит в равный ему угол. Отрезок переходит в отрезок.Отрезок переходит в отрезок. Длины всех отрезков изменяются в k раз.
A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″ title=»С О А В А1А1 В1В1 С1С1 A => A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″ > 7 С О А В А1А1 В1В1 С1С1 A => A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1 A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″> A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″> A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″ title=»С О А В А1А1 В1В1 С1С1 A => A 1 B => B 1 C => C 1 ABC => A 1 B 1 C 1″>
8 O D1D1 C1C1 DC P B M A A1A1 B1B1Задача: Дано: OMP Построить: квадрат ABCD, A OM, B MP, C OP, D OP Решение: 1) Строим квадрат A 1 B 1 C 1 D 1 : A 1 OM, C 1 OP, D 1 OP 2) OB 1 MP = B 3) BC OP, BA || OP, AD OP 4) ABCD – искомый квадрат