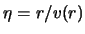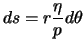Что такое годограф в сейсморазведке
Элементы теории сейсморазведки. Понятие о годографе и кажущейся скорости.
Одним из стержневых понятий в теории сейсморазведки является понятие годографа.
Зная положение точек наблюдения, в которых определено время прихода волны, можно составить зависимость t = 
.Зависимость времени прихода волны от координат точек наблюдения называют годографом.
Рассмотрим такую зависимость для прямой волны вдоль линии наблюдения OS лежащей на плоскости. На этой же плоскости находится источник колебаний (рис45).
Рис. 45. Поверхностный (а) и линейный (б) годографы прямой волны; поверхностные изохроны прямой волны (в)
Выберем систему координат так, чтобы начало ее находилось в точке возбуждения колебаний О. Рассматриваемая волна бежит вдоль поверхности от точки O к точке S, координаты которой x и y.
Из аналитической геометрии следует, что это уравнение конуса вращения. Ось вращения – ось t. Вращением системы координат можно совместить ось x с OS. Тогда y под корнем исчезнет и уравнение будет приведено к виду 
. Это уравнение прямой, исходящей из начала координат. У нее две симметричные относительно оси t ветви: 
и 
. Такое уравнение называется линейным продольным годографом прямой волны(Рис.45б). Геометрически это сечение конуса вращения (пространственного годографа прямой волны) вертикальной плоскостью, проходящей через начало координат. Непродольный линейный годограф получим, если линия наблюдения не проходит через О. Он будет представлять собой результат вертикального сечения конуса плоскостью, не проходящей через начало координат. Как известно, такое сечение представляет собой гиперболу (рис45а). Здесь точка О’ – проекция О на линию профиля l в плоскости XOY.С понятием годографа тесно связано понятие кажущейся скорости V *
Рис.46. К выводу закона Бенндорфа.
Наблюдателю, находящемуся на поверхности, кажется, что волна, двигаясь от P1 к P2 преодолела расстояние Δх вдоль поверхности наблюдения со скоростью, равной
V * = 
, где е – угол, дополняющий i до 90°. Такой угол называют углом выхода сейсмической радиации. Это выражение носит название закона кажущейся скорости или закона Бенндорфа.
Если эта волна движется вдоль поверхности наблюдения, то есть фронт волны перпендикулярен этой поверхности (α = 90°), то из выражения V * = 
следует, что V * = V (так как sin90°= 1). Так двигаются поверхностные волны-помехи и определенная по годографам этих волн V * будет как угодно близка к истинной, составляющей в приповерхностной части разреза 500-1000 м/сек. Если же волны приходят снизу, по направлению близкому к вертикали (фронт волны практически параллелен поверхности наблюдения), то V * →∞, поскольку α→0. Так двигаются полезные отраженные волны, откуда следует, что полезные волны те, которые имеют очень высокие кажущиеся скорости, превышающие, как правило, 5000 м/сек.
Сказанное означает, что можно по величинам кажущихся скоростей отделять полезные волны от помех, осуществлять их фильтрацию по кажущимся скоростям.
Проблема борьбы с помехами чрезвычайно актуальна и составляет главное содержание методики проведения полевых работ и обработки данных. Сами по себе возможности этой борьбы обусловлены тем, что каждая волна характеризуется своими кинематическими зависимостями, то есть формой годографа. Поэтому теория годографа – основной элемент теории сейсморазведки и исследователи заняты решением прямой и обратной кинематических задач сейсморазведки – получением уравнений годографов самых разных волн для самых разных моделей среды и исследованием этих уравнений. Уравнение годографа прямой волны мы уже рассмотрели выше. Остановимся теперь на годографах отраженных и преломленных волн. Для получения уравнения линейного продольного годографа в случае простейшей двухслойной модели среды обратимся к рис. 47.
 |
Пусть произвольный луч падающей волны касается границы R в точке R. Из этой точки отражения исходит колебание по лучу RS под углом, равным углу падения (рассматривается монотипная волна). Таким образом, уравнение времени по рассмотренному лучу может быть записано в виде (Рис. 47б)
Опустим из точки О нормаль на границу раздела R и продолжим за эту границу до пересечения с продолжением луча RS. Они пересекутся в точке О*, которая является зеркальным отображением О ( в зеркале границы R). Это можно доказать из рассмотрения треугольников ОRМ и О*RМ. Нетрудно показать, что они равны. Оба они прямоугольные, МR – общий катет, углы ОRМ и О*RМ равны, поскольку равны углу, дополняющему их до 90°. Следовательно равны катеты ОМ и О*М, представляющие глубину границы по нормали, и гипотенузы ОR и О*R. Таким образом, можно записать, что RS+ RO* = О*S, то есть можно представить лучи, исходящие из пункта возбуждения О через лучи, исходящие из О*. Точка О* называется поэтому мнимым пунктом возбуждения.
Итак, уравнение времени можно переписать в таком виде
О*S является гипотенузой большого прямоугольного треугольника О*О’S, где О’ – проекция точки О* на линию наблюдения. Следовательно О*S=
.
и уравнение годографа запишется в виде
Это уравнение гиперболы с минимумом над мнимым пунктом возбуждения.
Если положить х=0, то время t0 над точкой возбуждения колебаний (началом координат) окажется равным
При горизонтальном залегании границы R, то есть при равенстве угла φ нулю уравнение годографа отраженной волны примет вид
В этом случае точка минимума гиперболы окажется над пунктом возбуждения, тогда как при наклоне границы R она смещается в сторону восстания отражающей поверхности.
Поверхностный (пространственный) годограф ОВ нетрудно получить вращением гиперболы относительно вертикальной оси симметрии (параллельной оси времени), проходящей через точку О1 (рис.47а). Полученная фигура называется гиперболоидом вращения.
Годограф преломленной волны в системе ОТВ также нетрудно вывести, однако мы дадим его запись в готовом виде, а тех, кто затрудняется сделать самостоятельный вывод, адресуем к учебникам в списке литературы.
Если преломляющую границу считать горизонтальной, то есть положить φ=0, годограф преломленной волны примет вид
Рис.48. Годограф головной (преломленной) волны (плоская преломляющая граница, однородная покрывающая среда)
Геометрически это будут две симметричные ветви, исходящие из t0 с одинаковыми значениями x начальных точек выхода и с одинаковыми значениями времени 
в этих начальных точках.
В кинематической теории распространения волн рассматриваются и исследуются уравнения годографов всех перечисленных выше и иных волн, свидетельствующие об их существенных отличиях, что является основанием для выбора (селекции) этих волн, когда возникает такая необходимость. Определенные возможности такого выбора можно проиллюстрировать, рассмотрев вопрос о соотношении годографов основных типов волн, используемых в сейсморазведке: отраженных, преломленных и прямых все для той же простой двухслойной модели среды и для того же простого двумерного (плоского) случая. Для еще большей простоты положим, что отражающая (преломляющая) поверхность R горизонтальна (Рис.49 ).
Рис.49. Соотношение годографов основных типов волн.
Выпишем уравнения годографа всех трех, показанных на рис. 49 волн
Чтобы уяснить соотношение годографов прямых и отраженных волн, устремим в выражении для tотр х → ∞. Тогда любым конечным числом в том числе h (и 4h 2 ) в сравнении с ∞ можно будет пренебречь. Следовательно tотр → tпрям, откуда можно заключить, что на бесконечности эти годографы сходятся, неограниченно сближаются. То есть асимптотой годографа отраженной волны (гиперболы) является годограф простой волны (прямая). Такое соотношение называется асимптотическим приближением.
Чтобы уяснить соотношение годографов отраженной и преломленной волн, рассмотрим на рис.49 ситуацию вблизи падения волны под критическим углом. Очевидно, что последний докритический луч отраженной волны и самый первый луч головной практически совпадают (отличаются на бесконечно малую), значит и времена годографов отраженной и преломленной волны будут одинаковыми. Такой случай, когда кривая (гипербола – годограф ОВ) и прямая (годограф преломленной волны) имеют общую точку называется в геометрии касанием. Итак, годограф прямой волны в точке tнач касается годографа ОВ. Наконец, соотношение годографов прямой и преломленной волн – пересечение. Именно так классифицируется случай, когда две прямые на плоскости(плоскости годографа х,t) имеют общую точку. Нетрудно определить координаты этой точки, для чего необходимо приравнять правые части уравнения 1 и 3 положив х = х1.
, отсюда 
, то есть точка пересечения лежит на расстоянии от начала координат как минимум в два раза большем, чем глубина h исследуемой границы раздела R. Какие же практические выводы можно сделать из рассмотренного соотношения годографов? Их три.
1) Область примыкающая к источнику (вплоть до места сближения годографов всех трех волн) – это область работ методом МОВ. Здесь регистрации отраженных волн не мешают головные (они регистрируются на бо’льших удалениях), а от прямых волн отраженные отделены достаточно большим промежутком времени Δt (если граница залегает на глубине более 200-300м) и прямые волны успевают уйти от регистрирующих приборов. При мелком залегании такого промежутка Δt не будет и отраженные волны не удастся проследить уверенно.
2) область больших удалений от источника (>2h) это пространство, благоприятное для применения МПВ, поскольку преломленные волны регистрируются здесь в первых вступлениях, то есть приходят раньше всех других видов колебаний. Известно, что одной из главных задач, для решения которой применяется методика МПВ, является картирование рельефа поверхности кристаллического фундамента платформенных территорий. Глубина залегания фундамента на территории Восточно-Европейской платформы обычно не превышает 2,5-3 км. Это значит, что для регистрации первых вступлений преломленных волн от поверхности фундамента надо уходить на расстояние более 6-7 км от источника. В то же время, в Прикаспийской впадине, где глубины залегания фундамента оцениваются в 20-25 км, удаление должно составить более 50 км.
3) В области, где сближаются годографы всех волн и регистрируется очень сложная их интерференция (наложение) заниматься сейсмической разведкой вообще не рекомендуется.
Таким образом, рассмотренный вопрос о соотношении годографов основных типов волн приобретает отчетливое методическое значение и практический смысл.
Особенности кинематики волн в средах с криволинейными границами раздела.
Выявленные особенности кинематики различных волн относились к моделям двухслойной среды с плоской границей раздела. Во многих случаях такое упрощенное представление о форме границ вполне приемлемо – например, при изучении осадочных толщ на платформенных территориях. Однако, при работах в межгорных депрессиях или даже в платформенных регионах, но с развитой солянокупольной тектоникой, то есть в районах, отличающихся криволинейностью отражающих и преломляющих поверхностей, кинематика волн существенно искажается.
Рассмотрим простой пример. Пусть отражающая граница представляет собой элемент дуги окружности с центром на поверхности наблюдений и пусть в этом центре находится источник возбуждения колебаний.
Нетрудно убедиться, что в этом случае лучи (если среда однородная) геометрически будут радиусами этой окружности и при отражении сфокусируются в точке возбуждения О. При этом годограф отраженной волны вырождается в точку (рис.50а).
Если отражатель – окружность с центром – источником и этот источник находится на некоторой глубине под поверхностью наблюдений годограф ОВ будет представлять собой гиперболу, но с обратным соотношением абсцисс точек отражения и точек выхода лучей на поверхность: правая ветвь гиперболы будет отвечать левой стороне дуги отражательного элемента, а левая – правой, причем все отраженные лучи будут проходить через точку ПВ (центр окружности) – фокусироваться в ней.
Эти простые примеры позволяют понять, что криволинейные формы синклинального (вогнутого) характера (в межкупольной мульде) на годографах ОВ проявляются вследствие подобной фокусировки как петли, точки возврата и крестообразные заходы (рис 50а), причем донышко петли будет представлять собой донышко мульды, ее правая ветка после креста-пересечения соответствовать левому склону, а левая ветка правому склону; точки возврата I и II – это точки смены характера соответствия (прямого на обратное) упомянутых абсцисс точек отражения точкам выхода луча. В свою очередь на отражательных элементах выпуклого характера (куполах) будет отмечаться не фокусировка, а напротив, аномальное расхождение лучей. Если отражающий элемент имеет форму параболического зеркала, отраженные лучи становятся параллельными, а пути – одинаковыми. Годограф превращается в горизонтальную прямую tпр-const (рис.50в).
Рис.50.Годографы отраженных волн от криволинейных границ:
а-синклинали; б – дуги окружности; в- параболы.
Годограф сейсмических волн
Из закона Снелиуса следует, что сейсмический луч, направленный внутрь Земли, будет отклоняться от нормали к сферическому пласту, так как с увеличением глубины скорость упругих колебаний, за редким исключением, увеличивается. Поэтому сейсмический луч, который вышел из точки 
на поверхности Земли, погрузившись на некоторую глубину, снова выйдет на поверхность в точке 
, где поставим сейсмоприемник (сейсмостанцию). Другой луч из той же точки, почти совпадающий с первым, выйдет на поверхности в точке 
(рис.3).
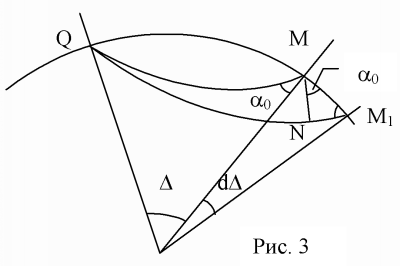
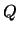
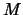
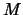
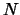
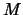
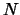
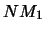
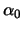
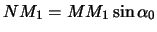
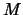
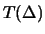
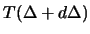
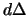
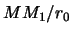
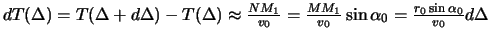
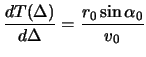Опустим перпендикуляр из точки на второй луч. Точку пересечения этого перпендикуляра с траекторией второго луча обозначим через 
. Точки , , образуют треугольник. Примем за основание этого треугольника сторону 
. Угол при вершине обозначим через 
— это угол падения первого луча на поверхность раздела, в частности, на поверхность Земли. Тогда увеличение пути второго луча по отношению к первому, будет равно 
. Пусть время, которое необходимо, чтобы волна достигла точки равно 
, а точки — соответственно 
, где 
— приращение эпицентрального расстояния, равное 
. Следовательно, 
. Отсюда следует
 | (2.5) |
В полученной формуле индекс «0» означает, что соответствующие величины относятся к приповерхностному слою на выходе сейсмического луча. Однако, можно показать, что величина приведенного отношения не изменяется вдоль всей траектории луча, он является параметром луча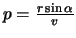 
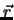
. Остается выяснить, каким образом с помощью параметра луча, который можно получить из годографа, определить изменение скорости в зависимости от радиус-вектора 
.
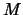
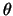
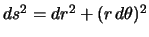
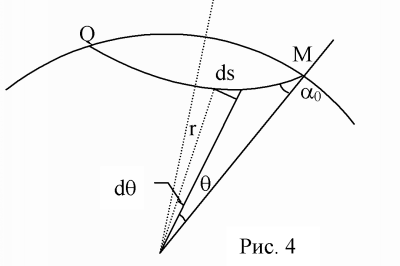
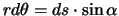
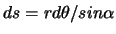
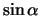
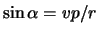
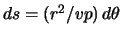
Обозначим изменение эпицентрального расстояния от текущей точки до точки через 
, тогда элементарную длину дуги на траектории луча можно определить из выражения 
, которое следует из элементарного треугольника, изображенного на рис.4. 
Но 
, поэтому 
. Выразим 
через параметр луча 
. Теперь 
. Введем обозначение
Теперь полученное выражение будет выглядеть так
Следовательно,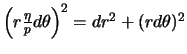 
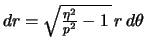
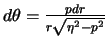
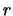
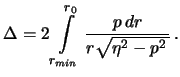. С помощью элементарных преобразований приходим к выражению 
. Следовательно, 
. Чтобы получить эпицентральное расстояние нужно проинтегрировать полученное выражение по 
от точки, где расстояние текущей точки на траектории луча находится на наименьшем расстоянии от центра сферы до точки на поверхности (точка выхода луча), а результат удвоить. Такая простая схема возникает лишь при гипотезе о сферически симметричной Земле, так как только в этом случае самая глубокая точка траектории делит ее пополам.
 | (2.6) |
Мы получили интегральное уравнение относительно функции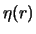 
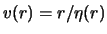
, с помощью которой легко определяется и скорость сейсмической волны: 
.
Один из примеров годографа приведен на рис.5.
 |
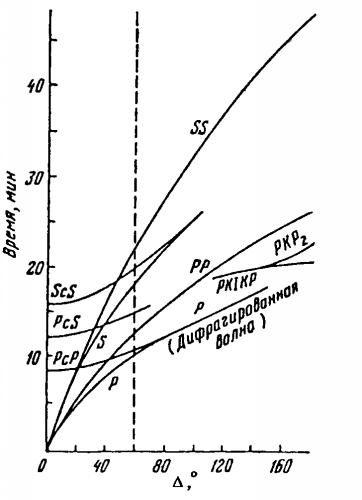| Рис. 5. |
Поля времён и годографы
Решение прямых кинематических задач заключается в установлении связи времени прихода t волны с пространственными координатами ПВ и ПП.
Зависимость времени от пространственных координат принято называть полем времён.
В общем случае поле времён есть функция от шести переменных, такое поле времён называется обобщённым: П33=txв,yв,zв,xп,yп,zп
Если зафиксировать какие-либо координаты, то из обобщённого поля времён получим локальныеполя времён:
●П22=txв,yв,xп,yп— при наблюдениях на горизонтальной плоскости;
●П21=txв,yв,zп— при наблюдениях в скважине;
●П12=tzв,xп,yп— при наблюдении на горизонтальной плоскости возбуждённых в скважине волн
Если ограничить пространство точек наблюдения, получим частныевременные поля. Частные временные поля принято называть сейсмическими годографами.
Сейсмический годограф – это зависимость времени t пробега упругой волны из ПВ в ПП от координат ПП относительно ПВ.
В теории сейсмических годографов местоположение источника часто принимают за начало системы координат. Для упрощения анализа чаще всего принимается допущение zп=0, т.е. поверхность наблюдений плоская.
Если наблюдения производятся на плоскости (xп, yп), то функцияt=fxп,yппредставляет собой поверхностный годограф. Проекции сечения поверхностного годографа плоскостями, перпендикулярными оси 0t, на плоскость 0xy, называются изохронами(линиями равных времён) поверхностного годографа сейсмической волны. Семейство изохрон образует карту изохрон.
Если наблюдения производятся вдоль некоторой линии, то:
(a)в случае, если линия ПП проходит через ПВ, эту линию называют линейным продольным профилем, а соответствующий годограф – линейным продольным годографом;
(b)в случае, если линия ПП не проходит через ПВ, эту линию называют линейным непродольным профилем, а соответствующий годограф – линейным непродольным годографом;
(c)в случае, когда ПВ расположен на поверхности, а приёмники – в скважине, зависимость t(zп) называют вертикальным, или скважинным, годографом. Если ПВ находится у устья скважины, имеем продольный вертикальный годограф,иначе – непродольный.
Время пробега волны зависит от ряда факторов:
●характер строения и скоростная модель распространения упругих волн в геологической среде
●положение и форма геологических границ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет