Что такое гмт в геометрии
Что такое гмт в геометрии
Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.
Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
К сожалению, не сохранилось первоисточников, описывающих ранний период развития греческой математики. Только благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.
Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний:
Геометрическое место точек (ГМТ).
Определения.
Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.
Название связано с представлением о линии как о «месте», на котором располагаются точки.
Примеры.
Пример 1.
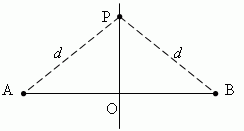
Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB :
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2.
Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.
Пример 3.
Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра ( на рис. показана одна из этих точек – А ).
Теоретическая часть.
Касательная. Предположим, секущая PQ ( рис.2 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
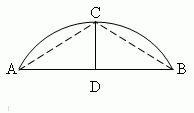
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.4 ). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.
Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.5 ).
Центральный угол – угол, образованный двумя радиусами ( ∠AOB, рис.5 ). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки ( ∠BAC, рис.4 ). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( ∠BAC, рис.3 ).
Соотношения между элементами круга.
Вписанный угол ( ∠ABC, рис.7 ) равен половине центрального угла, опирающегося на ту же дугу AmC ( ∠AOC, рис.7 ). Поэтому, все вписанные углы ( рис.7 ), опирающиеся на одну и ту же дугу ( AmC, рис.7 ), равны. А так как центральный угол содержит то же количество градусов, что и его дуга ( AmC, рис.7 ), то любой вписанный угол измеряется половиной дуги, на которую он опирается ( в нашем случае AmC ).
Все вписанные углы, опирающиеся на полукруг (∠APB, ∠AQB, …, рис.8 ), прямые.
Угол (∠AOD, рис.10), образованный двумя секущими ( AO и OD ), измеряется полуразностью дуг, заключённых между его сторонами: ( AnD – BmC ) / 2.
Угол (∠DCB, рис.11), образованный касательной и хордой ( AB и CD ), измеряется половиной дуги, заключённой внутри него: CmD / 2.
Произведения отрезков хорд ( AB и CD, рис.13 или рис.14), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO.
Квадрат касательной равен произведению секущей на её внешнюю часть ( рис.12): OA 2 = OB · OD. Это свойство можно рассматривать как частный случай рис.14.
Интересный факт:
Поздравляем с Пи-раздником вас.
Фанаты будут соревноваться, вспоминая знаки числа «Пи». И постараются превзойти рекорд 24-летнего китайского студента Лю Чао, который назвал по памяти без ошибок 68890 знаков. На это у него ушло 24 часа и 4 минуты.
Отмечать праздник придумал американский физик Ларри Шо (Larry Shaw).
На вопрос, сколько знаков в числе «Пи» после запятой, точного ответа нет. Скорее всего, их бесконечное число. А главная особенность в том, что последовательность этих знаков не повторяется. Сегодня их известно 12411 триллионов. Обследовано 500 миллиардов. И повторений не найдено.
Список использованных источников:
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Геометрическое место точек
Геометри́ческое ме́сто то́чек (ГМТ) — фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.
Примеры
Формальное определение
В общем случае, геометрическое место точек формулируется параметрическим предикатом, аргументом которого является точка данного линейного пространства. Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант 









В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.
Пример: параболу зададим как множество всех таких точек 














Презентация. Геометрия 7 класс. Геометрическое место точек
Описание презентации по отдельным слайдам:
Тема урока: Геометрическое место точек Геометрия – 7 класс Велиханова Марина Александровна, учитель математики КГУ «Банновская средняя школа», отдела образования акимата Федоровского района
Цели обучения: 7.1.1.31 знать определение геометрического места точек
1) На отрезке АВ найдите геометрическое место точки, равноудаленной от его концов. Геометрическое место точки, находящейся на отрезке и равноудаленной от его концов, есть середина отрезка. А В
2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка? А В
2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка? Геометрическое место точек, равноудаленных от концов отрезка – серединный перпендикуляр к отрезку А В
6 см О 4) Как выглядит ГМТ, расстояние от которых до заданной точки не больше 6 см? Кругом называют ГМТ, расстояние от которых до заданной точки не больше данного положительного числа.
Задачи на нахождение ГМТ Решение задачи на поиск ГМТ должно содержать доказательство того, что все точки фигуры, указанной в ответе, обладают требуемым свойством, а также наоборот, что все точки, обладающие требуемым свойством, принадлежат этой фигуре
Задача. Доказать, что биссектриса угла есть геометрическое место точек, равноудаленных от его сторон. 1) Построим CDBC, ADBA 2) BD-биссектриса CBD=ABDBCD=BAD AD = CD 3)KM = EM – доказывается аналогично А В С D M E K
ЗАПОМНИТЕ Самые известные примеры ГМТ. Геометрическое место точек, равноудаленных от концов отрезка, — серединный перпендикуляр к отрезку. Геометрическое место точек, удаленных от данной точки на заданное положительное расстояние, — окружность Геометрическое место внутренних точек угла, равноудаленных от его сторон, — биссектриса угла.
Задания для самостоятельной работы Желаю успеха!
Задание 1. Ответьте на вопросы. 1) Что, на ваш взгляд, является геометрическим местом точек, равноудаленным от данной точки? 2) Что будет являться геометрическим местом точек, равноудаленных от сторон угла? 3) Дайте определение геометрического места точек, равноудаленных от концов данного отрезка.
Задание 3. Можно ли круг радиуса 5 см считать геометрическим местом точек, удаленных от центра этого круга на расстояние: А) длиной 5 см; Б) не больше 5 см; В) не менее 5 см; Г) не больше 4 см? Нет Да Нет Нет
Задание 4. Отрезок AB равен 4 см. Можно ли считать срединный перпендикуляр этого отрезка геометрическим местом точек, которые: А) удалены от A и B на 2 см; Б) удалены от A и B на одинаковые расстояния; В)* являются вершинами равнобедренных треугольников с основанием AB? Нет Да Да
На уроке мы Познакомились с определением геометрического места точек Изучили самые известные пример ГМТ Рассмотрели задания на нахождение ГМТ
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1088497
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Дума проведет расследование отклонения закона о школьных онлайн-ресурсах
Время чтения: 2 минуты
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Пик использования смартфонов приходится на 16 лет
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК
понятие, иногда используемое в геометрии. Обычно под Г. м. т. понимают множество точек (образующих кривую или поверхность), выделяемых из всех точек пространства к.-л. геометрич. требованием. Напр., эллипс может быть определен как Г. м. т. плоскости, для к-рых сумма расстояний до двух данных точек есть величина постоянная. А.
Смотреть что такое «ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК» в других словарях:
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК — ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК, в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее… … Научно-технический энциклопедический словарь
геометрическое место точек — местоположение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы местоположение EN locus … Справочник технического переводчика
Геометрическое место точек — (ГМТ) фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством. Примеры Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов… … Википедия
кривая круговых точек — circle point curve Геометрическое место круговых точек на движущейся плоской фигуре. Шифр IFToMM: 2.3.31 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
Середина моста — геометрическое место точек, равноудаленных от начала и конца моста. Источник: Справочник дорожных терминов … Строительный словарь
Середина пролета — геометрическое место точек, равноудаленных от смежных опорных частей. Источник: Справочник дорожных терминов … Строительный словарь
График LM(LM SCHEDULE) — геометрическое место точек всех комбинаций уровней реального дохода и процентных ставок, соответствующих состоянию равновесия на денежном рынке … Современные деньги и банковское дело: глоссарий
кривая инверсии — Геометрическое место точек на термодинамической диаграмме, отображающих состояния вещества, в которых дроссельный эффект меняет свой знак … Политехнический терминологический толковый словарь
кривая фазового равновесия — Геометрическое место точек, отображающих на термодинамической диаграмме состояния сосуществующих фаз … Политехнический терминологический толковый словарь
КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… … Энциклопедия Кольера