Что такое глазковая диаграмма
Межсимвольные искажения. Глазковая диаграмма
При пропускании сигнала через канал с ограниченной полосой, либо фильтр, возникают межсимвольные искажения (межсимвольная интерференция).
Рассмотрим линейную цепь (см. рисунок ниже), где на вход поступают дискретные импульсы. Данные импульсы можно рассматривать как носители информации: положительные импульсы передают «1», а отрицательные соответственно «0».
Каждый импульс вызывает отклик фильтра. Если в момент следующего импульса, отклик фильтра от предыдущего фильтра не погашен, то сигнал становится помехой сам себе, что и называется межсимвольными искажениями. Таковой линейной цепью могут выступать формирующий фильтр передатчика, фильтр селекции приемника, многолучевой канал связи и т.п.
На рисунке ниже представлена осциллограмма сигналов на входе и выходе фильтра. Межсимвольные искажения привели к тому, что амплитуда отдельных импульсов уменьшилась вдвое. Это приведёт к тому, что после добавления шума, импульсы с малой амплитудной будут больше подвержены ошибкам.
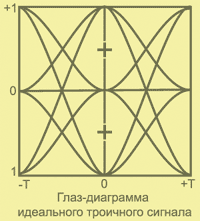
Глазковая диаграмма
Контроль межсимвольных искажений удобно производить по глазковой диаграмме.
Глазковая диаграмма – это интерференционное изображение, возникающие при наложении большого числа периодов цифрового сигнала.
Именно такое изображение покажет осциллограф, на вход которого подается псевдослучайный сигнал, а развертка по горизонтали которого равна длительности символа.
Процесс формирования глазковой диаграммы можно представить следующим образом: предположим, что осциллограмма сигнала нарисована на прозрачной пленке, если пленку с осциллограммой горизонтально порезать на кусочки, где ширина каждого кусочка равна длительности одного символа, и затем эти кусочки наложить один на другой, то получится глазковая диаграмма.
Ширина раскрытия глазка посередине диаграммы показывает размах наименьших по амплитуде импульсов (символа). Чем меньше раскрыт глаз диаграммы, тем больше межсимвольные искажения.
Необходимость символьной синхронизации
Выборка сигнала должна производиться в момент максимального раскрытия «глазка», когда межсимвольные искажения минимальны.
Если момент выборки запаздывает или опережает, то на устройство принятия решения поступает сигнал уменьшенной амплитудной, а значит и меньшим отношением с/ш.
В следующей статье подробнее рассмотрим тему «Фильтр Найквиста».
Анализ методов оценки качества сигнала: глаз-диаграмма, коэффициент битовых ошибок
Рассмотрим и проанализируем существующие методы оценки качества сигнала.
ГЛАЗ-ДИАГРАММА
Удобным (и гениально простым!) графическим методом оценки качества цифрового сигнала на выходе регенератора является глаз-диаграмма. Она представляет собой результат наложения всех возможных импульсных последовательностей в течение промежутка времени, равного двум тактовым интервалам линейного сигнала.
КОЭФФИЦИЕНТ БИТОВЫХ ОШИБОК
Необходимо отметить, что при прочих равных условиях BER зависит от количества переданных битов. Например, длинная последовательность одинаковых символов может вызвать низкочастотную амплитудную модуляцию и детерминированный джиттер, следствием которых будет рост числа ошибок. Для обеспечения корректности сравнения разных ЦСП используются типовые испытательные последовательности, причем каждой стандартной скорости передачи соответствует своя испытательная последовательность. По своим свойствам они близки к гауссову шуму, но имеют определенный период повторения. Поэтому они называются не просто случайными, а псевдослучайными последовательностями (ПСП) (Pseudo-Random Bit Sequence, PRBS).
Следует особо подчеркнуть, что оценка BER будет абсолютно точной только при бесконечно большом числе переданных битов. Строго говоря, когда их число ограничено, мы получаем не вероятность события BER, а его оценку BERT. Очевидно, что уровень достоверности этой оценки (Confidential Level, CL), называемый также доверительной вероятностью, зависит от количества зарегистрированных ошибок и от общего числа переданных битов N.
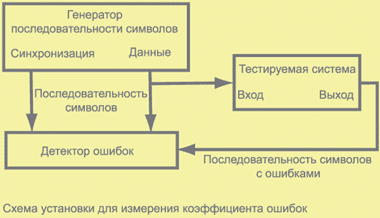
Типовая схема измерения BER предполагает наличие генератора испытательных битовых (символьных) последовательностей тестера BER, испытуемого объекта (регенератора, участка ЦСП и т. д.) и детектора ошибок тестера BER.
Генератор тестера BER формирует испытательные сигналы, которые подаются на вход тестируемого объекта. Генератор тестируемого сигнала является также источником сигнала для детектора ошибок тестера BER.
Тестируемый объект может быть территориально совмещен с тестером BER или находиться в удаленном пункте. В любом случае испытуемый объект должен быть выведен из эксплуатации и сигнал с его выхода подан на вход приемника тестера BER. Как говорят связисты, должен быть организован измерительный шлейф.
Детектор ошибок получает испытательный сигнал с выхода тестируемого объекта или формирует точную копию этого сигнала автономно. Испытательный сигнал генератора сравнивается побитно с сигналом, поступающим с выхода испытуемого объекта. Каждое различие сигналов детектор фиксирует как битовую ошибку.
Необходимую синфазность двух указанных сигналов обеспечивает детектор ошибок, в котором предусмотрена требуемая задержка сигнала с выхода генератора. Задача фазирования сигналов обычно выполняется на этапе калибровки тестера BER.
В генераторах тестеров BER предусмотрена возможность создания произвольных испытательных последовательностей, называемых обычно кодовыми словами.
Очевидным недостатком BER является необходимость вывода тестируемого объекта из эксплуатации (Out of Service, OoS), что вполне приемлемо в процессе разработки или ремонта объекта и неудобно, если ЦСП уже эксплуатируется. Кроме того, параметр BER хорош для оценки влияния одиночных помех, обусловленных гауссовыми процессами, например собственными и переходными помехами. В то же время в любой реальной системе связи присутствуют и целые пакеты таких ошибок (их еще называют серийными ошибками). Поэтому без знания временной структуры ошибок системы связи невозможна эффективная локализация повреждений и накопление адекватной информации о качестве разработки и инсталляции оборудования. По сути, одного параметра BER недостаточно для корректной оценки работы ЦСП. Необходимы более адекватные, учитывающие структуру помех, показатели качества ЦСП с возможностью их мониторинга в процессе нормальной эксплуатации системы связи (In Service Monitoring, ISM). Такие как рекомендации G.821 и G.826.
Таблица 1. Требуемые значения нормированной длительности.
Методы измерения шума в цифровых схемах
В статье рассмотрены методы оценки джиттера в канале передачи. Отмечены достоинства и недостатки каждого подхода.
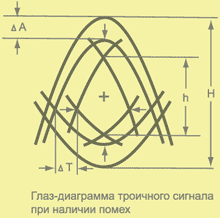
Для определения параметра BER наиболее информативно место пересечения глазков. На рисунке 2 изображена глазковая диаграмма и гистограмма распределения выборок в точке пересечения. Гистограмма представляет собой распределение вероятности появления ошибки. На рисунке 3 показана область перехода на глазковой диаграмме и соответствующая гистограмма ошибки временного интервала (TIE — Time Interval Error). На глазковой диаграмме прослеживаются две отдельные линии фронтов и спадов, что указывает на присутствие в канале систематического шума. Размытость линий свидетельствует о наличии случайного шума. На гистограмме четко видны две области с максимальной вероятностью неверного распознавания бита.
При анализе величины BER с помощью гистограммы следует иметь в виду, что результат измерения во многом зависит от длительности тестирования. Так, значение BER, полученное при быстром анализе, будет значительно отличаться от значения, полученного на том же анализаторе, но после нескольких часов непрерывного измерения. В связи с этим в некоторых стандартах требуемый уровень BER приводится с указанием времени измерения.
Часто при анализе шума удобно использовать U-образную кривую. Она представляет собой график зависимости частоты появления ошибочных битов (BER) от положения пробной точки на единичном интервале (Т). В области пересечения на глазковой диаграмме BER = 0,5 (равная вероятность правильного и неверного определения бита). В этой области преобладает механизм детерминированного джиттера, кривая идет полого (моменты Т = 0 и Т = ТВ на рисунке 4). По мере продвижения пробной точки к центру единичного интервала BER стремительно уменьшается, и усиливается влияние случайного шума. Оптимальное положение пробной точки — в центре единичного интервала (глаза).
Помехоустойчивость системы определяется расстоянием между ветвями U-образной кривой. Чем дальше находится левая ветвь кривой от правой при определенном BER, тем больше запас устойчивости к джиттеру.
Если мысленно сделать горизонтальный разрез области перехода на глазковой диаграмме, то будет получен профиль распределения битов. Второе измерение, которое проводится по глазковой диаграмме, делается относительно вертикального разреза в центре глаза. Полученный профиль позволяет судить о величине шума в канале и оценить его влияние на качество связи.
На рисунке 5 показано распределение BER в области перехода на глазковой диаграмме и на пологой вершине. Комбинируя эти измерения, можно получить контур вероятности появления ошибки (BER Contour). Многие цифровые осциллографы, тестеры и анализаторы шума имеют такую функцию. Для построения линии BER пробная точка смещается по всему глазу, делая разрезы под произвольными углами (см. рис. 6).
Глазковые диаграммы и BER(bit error rate)
Для анализа высокочастотных цифровых схем часто применяются глазковые диаграммы, в этой статье описаны базовые принципы построения глазковых диаграмм и как с помощью них получить информацию о дефектах в спроектированной системе. Так же поговорим о недостатках данного метода измерения и что применяется для анализа по мимо глазковых диаграмм.
Глазковая диаграмма
Для начала необходимо понять, как же строится глазковая диаграмма.
Типичная диаграмма выглядит следующим образом(источник):
Построение глазковой диаграммы
Для построения диаграммы не обязательно иметь дифференциальный сигнал, её вполне можно построить и с помощью single ended сигнала. Для построения глаза необходимо через тракт прогнать определённую последовательность, которая сформирует картину, похожую как на рисунке сверху.
Рассмотрим минимальный набор информации, которая должна пройти через тракт, для построения глаза.
Теперь мысленно просуммируем все последовательности и получим:
Осциллограф, накапливает данные, наслаивая их друг на друга, и в результате получаем что то похоже, как на рисунке в начале статьи.
Визуальный анализ глазковой диаграммы
Вернёмся к реальным диаграммам и возьмём для примера эту(источник):
Глазковая маска(eye mask) — по сути некий паттерн который можно задать в настройках осциллографа, для вывода вместе с диаграммой. Зачем он нужен? Всё очень просто, ряд стандартных интерфейсов имеют требования по качеству цифрового тракта на разных концах линии передач(например у передатчик и у приёмника, до кабеля и после). Для определения качества тракта, задаётся некая строго определённая маска(а если быть конкретнее точки для её построения) в пределы которой не должен попадать ни один сигнал из той выборки. Например, по рисунку выше, можно сказать, что тест пройден успешно.
А вот пример с явными проблемами(источник):
Как видно, сигнал касается и пересекает маску, и по этому делается вывод о некачественном цифровом тракте.
Примеры точек для задания маски в глазковой диаграмме можно посмотреть в спецификации USB, параграф «High-speed Signaling Eye Patterns and Rise and Fall Time».
Уровень шума(noise amplitude) — это толщина отрисованной линии на осциллографе в тех временных областях, где закончились переходные процессы, или другими словами, там где сигнал может быть чётко определён (0 или 1). Чаще данный параметр используется для расчёта других показателей, которые считаются осциллографом автоматически. Например, добротность(Q-factor). Если коротко, то чем ниже Qf, тем хуже качество глазговской диаграммы. Вот наглядный пример(источник):
Иногда в литературе можно встретить параметр SNR, но это тоже самой что и добротность в глазковых диаграммах.
Дрожание и cross over area — в глазковой диаграмме дрожание можно определить по толщине области пересечения (cross over area). Понятное дело, что чем данная область тоньше, тем лучше. Но есть несколько нюансов.
Один из нюансов заключается в следующем: желательное пересечение фронтов всегда происходило на центральной оси глаза, как показано на рисунке ниже.
Причина по которой может происходить пересечение не в центре, это разбаланс драйвера, при котором время длительности логической 1 превышает время длительности логического нуля(или на оборот). Ниже приведён наглядный пример c пересечением в центре(слева) и пересечением выше центральной оси(справа). Берём две последовательности сигнала где логическая 1 по времени превышает логический 0 и получаем Cross over 80%.
Второй нюанс — плотность дрожания должна возрастать без перепадов к центру пересечения нарастающих и спадающих фронтов. Если ещё раз обратить внимание на диаграмму ниже, видно как в центре, диаграмма имеет ярко выраженный красный цвет, хотя по краям жёлтый, перетекающий в синий.
Оценка характера возрастания плотности пересечений в cross over области по цвету является весьма поверхностным анализом. Для этого специально придумали метрику/метод измерения — bit error rate(BER), поговорим о нём подробнее в следующем параграфе.
Анализ глазковой диаграммы с помощью Bit Error Rate
Основы
BER это число, которое показывает отношение бит принятых с ошибкой к общему числу отправленных бит данных:
Анализ
Как уже писалось выше, BER можно использовать для исследования глаза в областях пересечения, а если быть точнее, то исследование сводится к изучения характеристик джиттера. Давайте рассмотрим область пересечения ближе, держа в уме формулу для определения BER. Представим, что мы отсняли глазковую диаграмму, далее в произвольное место вблизи пересечения помещаем точку в которой будет считаться BER. Вот например как тут:
Понятно, что в точке как на рисунке выше BER = 0. Интересующая нас область находится левее. Будем двигать точку влево, до тех пор пока не найдём такое положение, где BER = 1.
Если кривая BER не имеет локальных максимумов/минимумов, можно говорить о том, что нет аномалий в джиттере.
Точно такое же необходимо провести для второго края, в данном случае правого пересечения. В идеале, зависимость BER должна быть одинакова с обоих краёв, как на рисунке ниже(источник):
Недостаток глазковых диаграмм в анализе качества цифрового тракта.
При отрисовки глазковой диаграммы, как правило используется небольшое число бит, одна из основных причин — это память осциллографа. Если рассматривать возникновение ошибки с точки зрения вероятности, то становится очевидно — чем меньше число бить, тем сложнее обнаружить редкую ошибку.
Bit Error Rate Test
В основе Bit Error Rate Test лежит измерение параметра BER. Как посчитать BER выше уже писалось, но повторение мать учения.
BER это число, которое показывает отношение бит принятых с ошибкой к общему числу отправленных бит:
Постановка задачи.
Предположим у нас есть железка с высокоскоростным интерфейсом. Необходимо проверить качество передачи по цифровому каналу. Обычно задаются конкретным верхним порогом BER, и проверяют превышает ли конкретный образец заранее заданное значение верхнего порога BER.
Когда речь идёт о малых количествах ошибок при большом трафике, можно сказать, что возникновение ошибки в тот или иной момент времени имеет вероятностный характер. Для нас это означает следующие: нельзя взять железку, подключить измерительное оборудование, запустить тест, поковырять в носу и остановить тест зафиксировав значение BER. Почему нельзя? А нельзя потому, что возможно передалось слишком малое количество бит за отведённый промежуток времени, и из за низкой вероятности появления ошибок, они толком не успели появится, и тест покажет отличный BER.
Допустим мы выяснили — лучше подождать подольше, тогда измерительный стенд выдаст BER, максимально приближенный к реальности. Это допустимо? Да, но только когда у вас одна железка и вагон времени… Что делать с большой партией которую необходимо проверить? Об этом поговорим в следующем параграфе.
Определение времени тестирование или какое количество бит передать через цифровой канал?
Мы принимаем тот факт, что появление ошибки для нас являются случайной величиной. Раз так, то в дальнейшем, мы будем рассматривать данный вопрос с точки зрения теории вероятности. Для удобства введём такое понятие как статистический уровень доверия (в литературе встречается как SLC).
Статистический уровень доверия — это вероятность, что фактическая вероятность больше чем некая константа, которую мы задали.
Фактическая вероятность — вероятность которая была получена при очень большом количестве(стремящимся к бесконечности) экспериментов.
Немного забегая вперёд, SLC по сути показывает, на сколько мы можем доверять нашей вероятности появления ошибок(BER) при определённом количестве тестов. Мы будем задавать разный уровень доверия, и наблюдать как меняется количество бит, которые необходимо передать в ходе тестирования.
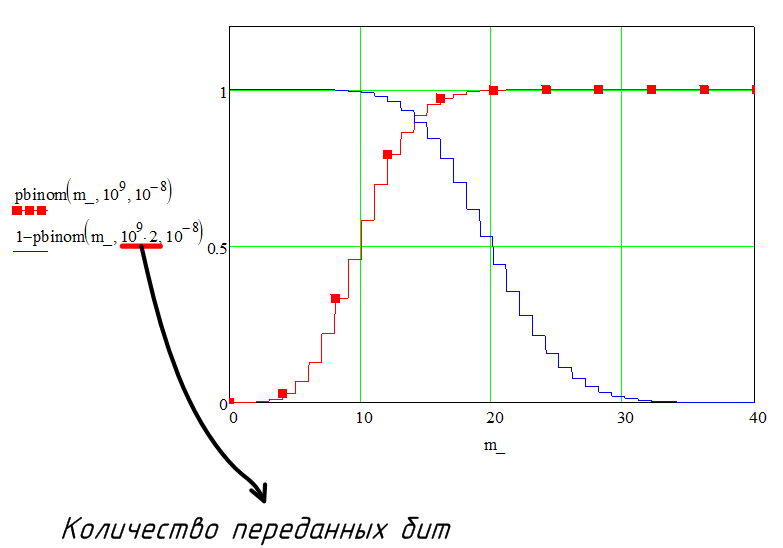
Итак, все расчёты будут вестись на основе биномиального распределения. По сути биномиального распределение — это распределение вероятностей возникновения какого либо события n раз. Сразу для примера, построим биномиальное распределение вероятностей встретить n ошибочных битов при передачи 10^ <9>бит в системе, вероятность ошибки 10^ <-8>.
Из рисунка видно, что вероятность встретить 0 ошибочных бит как и 20 очень мала. А вот максимальная вероятность приходится на n = 10.
Опишем, что скрывается за функцией dbinom. Данная функция, для каждого n, считает вероятность по формуле Бернули:
\LARGE P = С_
Где P — Вероятность, что в k независимых испытаний, некое случайное событие наступит ровно m раз. В случае биномиального распределения, данное событие считается для каждого m.
p — вероятность наступления событие единичной попытки.
q — вероятность, что событие не наступит при единичной попытки. Для q верно: q = 1-p.
Тут надо отметить, что если мы возьмём и посчитаем вероятности для большого числа k, и просуммируем их, то получим 1(ну или число очень близкое к 1). Изобразим это на графике:
График выше можно читать следующем образом: вероятность того, что мы обнаружим 15 бит или меньше при передаче 10^ <9>бит равна примерно 90%.
Теперь ещё раз вспомним постановку задачи. Нам необходимо найти количество бит, которые нужно передать, чтобы наш BER был близок к истинному BER. Держа это в уме, и что функция pbinom возвращает вероятность встретить m ошибок или менее. Можно сказать, что 1 — pbinom = SLC. Для наглядности построим всё это на одном графике.
Теперь мы говорим, что для SLC = 95%, нас устраивает если на 5 ошибочных битов приходилась почти вся вероятность(красный график). В данном графике это не так, поскольку мы передали через систему слишком маленькое количество бит. Давайте увеличим количество переданных бит.
Теперь SLC = 95% нас удовлетворяет т.к. в него укладывается почти все возможные m.
Теперь запишем всё это математически, при этом я опустил вывод формулы для n(количество необходимых бит). Скажу лишь, что при вычисление допустимо применять теорему Пуассона. Формула для n выглядит следующим образом:
\LARGE n = \frac<1>
Это уравнение справедливо для количества найденных ошибок равно 0(полное уравнение по ссылке). Почему 0? Всё очень просто, обычно у правильно спроектированной системы BER является на порядок ниже, чем того требует стандарт. Поэтому в этом уравнение, BER задаётся стандартом, и т.к. мы предполагаем что в тестируемой системе BER ниже, чем того требует стандарт, следовательно вероятность обнаружить 0 ошибок действительно велика.
Теперь давайте предположим, что нам необходимо подтвердить, что наша система удовлетворяет BER = 10^ <-12>с SLC = 98%. В таком случае n = 3.9 \cdot 10^ <12>бит будет достаточно. И если данные требования предъявляются для системы с скоростью передачи 1ГБит/с тогда время тестирования составить примерно 3900 секунд.
Реально ли серийные образцы тестируют так долго? Конечно же нет, если тестирование получается таким долгим, то в сигнал намеренно добавляют шум, чтобы увеличить BER и уменьшить время тестирования. Но это уже отдельная тема, здесь мы её касаться не будем.
Глазвовая диаграмма простой метод тестирования и анализа цифрового тракта, который позволяет выявлять грубые ошибки в проектирование.
Для более точного оценки качества системы коммуникации используют параметр BER, для данного теста необходимо более дорогостоящие оборудование и большое время на тестирование одного образца, но тем не менее есть методики, которые поваляют сократить время тестирования. При BER тестах, необходимо аккуратно подходить к выбору времени тестированию одного образца т.к. в случае неправильного выборе времени, можно сделать неправильный вывод о качестве изделия.
ИССЛЕДОВАНИЕ МЕТОДА ГЛАЗКОВЫХ ДИАГРАММ ДЛЯ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА БИТОВЫХ ОШИБОК В ЦИФРОВЫХ СИСТЕМАХ СВЯЗИ
В данной статье рассмотрен метод выявления коэффициента ошибок в канале связи с помощью глазковых диаграмм. В программном пакете MATLAB смоделирована схема для измерения коэффициента ошибок.
Ключевые слова: глазковая диаграмма, вероятность ошибки, коэффициент битовой ошибки, помехоустойчивость.
Сфера телекоммуникаций является важной частью человечества, поскольку представляет собой возможность общения людей друг с другом. На сегодняшний день это наиболее перспективное направление в науке, которое продолжает развиваться.
Одно из требований к сетям обмена информацией – точность приема этой информации. Сейчас практически все системы связи являются цифровыми. Повышение точности приема информации тесно связано с помехоустойчивостью системы. А, в свою очередь, характеристикой помехоустойчивости является коэффициент битовых ошибок (BER – bit error rate). Вычисление коэффициента ошибок является наиболее эффективным способом для оценки функционирования системы.
Так как радиоканал сети связи является менее защищенным, чем кабельная система передачи информации, вычисление количества ошибок в такой системе будет актуальным.
1. Определение коэффициента ошибок.
Для начала стоит определить, что коэффициент битовых ошибок – это некоторая величина, которая помогает оценить помехоустойчивость системы связи. И чем меньше BER, тем лучше работает система, и тем менее она будет восприимчива к воздействию внешних помех.
По определению коэффициент битовых ошибок является отношением ошибочно принятых битов к общему количеству переданных битов.
где n – количество ошибок;
N – количество переданных битов.
Как правило, коэффициент битовых ошибок является оценкой вероятности ошибок в приеме бита.
2. Основы метода глазковых диаграмм.
Принцип работы схемы, представленной на рисунке 1, заключается в том, что поток бит подается на осциллограф, пока синхронизация внешней развертки осуществляется от битового потока с частотой fb. Если требуется построение многоуровневых диаграмм, то сигнал дополнительно направляют на многоуровневый конвертер, а синхронизация осуществляется от символьного потока с частотой fs.
Рис. 1. Схема построения глазковых диаграмм
Построение глазковой диаграммы
С точки зрения исследования глазковая диаграмма – это изображение на экране осциллографа в виде результата наложения импульсных сигналов друг на друга, часто с применением режима персистенции (запоминания осциллограмм на некоторое время) и с нормированием масштабов осциллограмм сигналов. В процессе передачи сигнала по каналу связи импульс искажается. И по мере этих искажений можно делать выводы о параметрах канала связи. [1]
Рис. 2. Глазковая диаграмма двухуровневого сигнала
Расстояние B характеризуется, как раскрыв глазковой диаграммы, определяется между двумя ближайшими уровнями реализаций сигнала и соответствует значению коэффициента интенсивности битовых ошибок. Расстояние B/2 является запасом помехоустойчивости регенератора, который равен минимальному дополнительному уровню шума, который может вызывать ошибку. Максимальный запас помехоустойчивости обеспечивается, в случае когда принятие решения о переданном бите информации производится в определенный момент времени iT. [2]
3. Реализация метода глазковых диаграмм.
Целью данной работы являлось моделирование канала связи и определение коэффициента ошибок по методу глазковых диаграмм. Для наглядного представления метода глазковых диаграмм исследование было проведено в программном пакете MATLAB с использованием канала с аддитивным белым гауссовским шумом. В цифровой системе передачи, чтобы описать гауссовский шум, используют распределение Гаусса.
где: µ – математическое ожидание; σ – среднеквадратическое отклонение.
Схема реализации поставленной задачи приведена на рисунке 3.
Рис. 3. Схема исследования в Simulink
В исследуемой схеме сигнал задается генератором случайных последовательностей и преодолевает свой путь, начиная с конвертации в биполярный вид (Unipolar to Bipolar Converter), затем, разделяясь на две ветви, следует на модулятор с минимальным частотным сдвигом (MSK) и с минимальным гауссовским сдвигом (GMSK). Пройдя через модуляторы, сигнал попадает в канал с аддитивным белым гауссовским шумом (AWGN) для имитации условий прохождения сигнала по каналу, близких к реальным. Далее установлены два осциллографа глазковых диаграмм (Eye Diagram), с помощью которых можно оценить интенсивность битовых ошибок. Затем сигнал проходит через демодуляторы и обратно конвертируется в однополярный вид, после чего можно пронаблюдать результат на осциллографах (Time Scope).
Полученные глазковые диаграммы представлены на рисунках ниже (Рис.4, Рис.5).
Рис. 4. Глазковая диаграмма по ветви с GMSK модуляцией
Рис. 5. Глазковая диаграмма по ветви с MSK модуляцией
В идеале глазковая диаграмма, исходя из названия, представляет собой «раскрытый глаз», так как получилось на рисунке 7 при MSK модуляции. На рисунке 6 при другой ветке модуляции видим очевидное наложение волн друг на друга – явление интерференции. Анализируя подобные глазковые диаграммы, можно определить коэффициент интенсивности битовых ошибок, значение которого соответствует расстоянию между низким и высоким глазковыми уровнями. Такое расстояние называется вертикальным глазковым открытием. Обратим внимание, что поставленный блок счетчика ошибок показывает значение 0.28409, что допустимо при передаче сигнала при моделировании на компьютере.
4. Заключение.
Бесперебойная и точная передача данных всегда являлась главной задачей в телекоммуникационной сфере. Однако не всегда нам удается передать данные безошибочно. Для того чтобы регулировать измерение коэффициента ошибок в системе, метод глазковых диаграмм является удобным, нетрудным и неутомительным. Простота реализации с помощью пакета MATLAB является преимуществом перед другими методами выявления ошибок.