Что такое гипербола в математике как выглядит
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| 0,5 | 8 | 1 | 4 | 2 | 2 | 4 | 1 | 8 | 0,5 | fpm_start("true"); Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y. Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено. Пример 2Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже: Гипербола в математикеГипербола (в математике) — это две кривые, которые похожи на бесконечные луки, зеркально повторяющие друг друга. Гипербола — это множество точек плоскости, для которых модуль разности расстояний от двух данных точек (F1 и F2 на рисунке, называемых фокусами гиперболы) — это величина постоянная и меньшая, чем расстояние между фокусами. F1 и F2 — фокусы гиперболы. Из определения гиперболы мы знаем, что модуль разности расстояний от фокусов гиперболы — это величина постоянная, это означает: |MF1 − MF2| = константа; т. е. расстояние от (M до F1) минус (M до F2) всегда будет постоянной величиной (константой; постоянной; цифрой с определённым числовым значением). Каноническое уравнение гиперболыКаноническое уравнение гиперболы выглядит так: Где a и b — длины полуосей (действительной и мнимой); т. е. a = расстояние от 0 до а и b = расстояние от 0 до b, как показано на этом рисунке: Примечание: уравнение аналогично каноническому уравнению эллипса (x²/a² + y²/b² = 1), разница в сложении вместо вычитания. Эксцентриситет гиперболыЭксцентриситет (обычно обозначаемый буквой е) показывает, насколько гипербола является «некривой», т. е. чем он ближе к 1, тем более вытянут её прямоугольник в направлении оси (меньше углы, образуемые асимптотами) и тем больше эта гипербола будет «растягиваться» вдоль своей действительной оси. Эксцентриситет гиперболы всегда больше 1. (величина отрезка F1F2 = 2c; c = расстояние от нуля до F1 и, соответственно, от нуля до F2) M — точка на кривой; N — точка на директрисе (отрезок MN перпендикулярен директрисе). Эксцентриситет (обозначаемый буквой е) является соотношением MF1/MN и имеет формулу: ПараболаПарабола — это геометрическое место точек, где любая точка находится на одинаковом расстоянии от: данной точки (фокус) и данной прямой (директриса). У параболы квадратичная функция вида: Что такое гиперболаСтатья находится на проверке у методистов Skysmart. Понятие гиперболыГипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами. Каноническое уравнение гиперболы в алгебре выглядит так: , где a и b — положительные действительные числа. Кстати, канонический значит принятый за образец. В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней. Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи. Вспомним особенности математической гиперболы: Если гипербола задана каноническим уравнением, то асимптоты можно найти так: Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
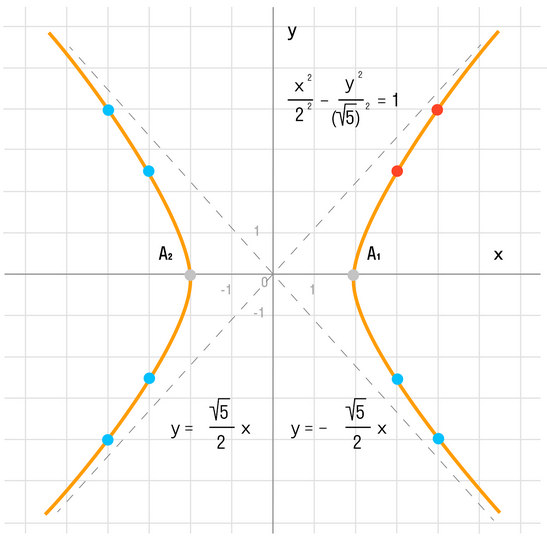
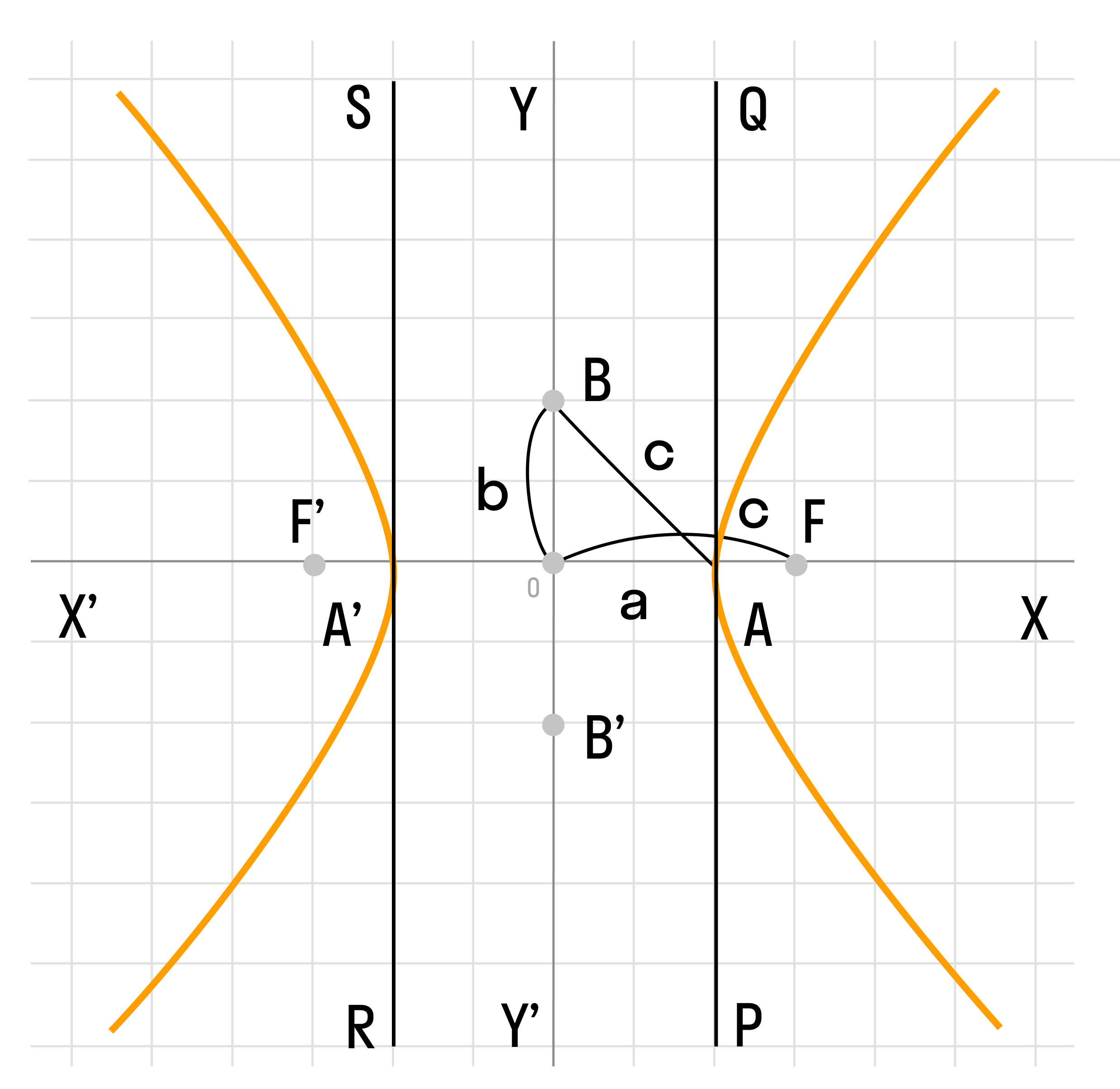
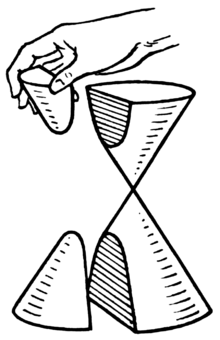
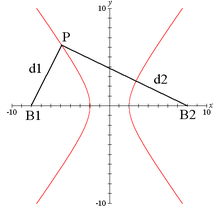
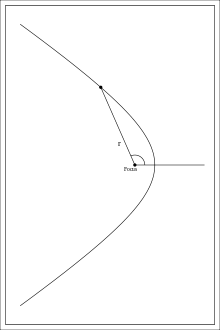
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0). В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти. Способ такой же, как при построении эллипса. Из полученного канонического уравнения на черновике выражаем: Уравнение распадается на две функции: — определяет верхние дуги гиперболы (то, что ищем); — определяет нижние дуги гиперболы. Далее найдем точки с абсциссами x = 3, x = 4: Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема. Действительная ось гиперболы — отрезок А1А2. Расстояние между вершинами — длина |A1A2| = 2a. Действительная полуось гиперболы — число a = |OA1| = |OA2|. Мнимая полуось гиперболы — число b. В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся. Форма гиперболыПовторим основные термины и узнаем, какие у гиперболы бывают формы. Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы. Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы. Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы. Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию. Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола. Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2. Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно. Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике. Фокальное свойство гиперболыТочки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы). Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы. Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы: Рассмотрим, как это выглядит на прямоугольной системе координат: Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем: Запишем это уравнение в координатной форме: Избавимся от иррациональности и придем к каноническому уравнению гиперболы: , т.е. выбранная система координат является канонической. Директориальное свойство гиперболыДиректрисы гиперболы — это две прямые, которые проходят параллельно оси. ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают. Директориальное свойство гиперболы звучит так: Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e. Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат. На самом деле для фокуса F2 и директрисы d2 условие можно записать в координатной форме так: Построение гиперболыЧтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему. Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы. В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции: Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график: Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу. По определению эксцентриситет гиперболы равен Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с. Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной. Гипербола (математика) Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы. СодержаниеИсторияТермин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком. ОпределенияГипербола может быть определена несколькими путями. Коническое сечениеГипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами. Как геометрическое место точекЧерез фокусыГипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна. Для сравнения: кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини. Через директрису и фокусГеометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная Связанные определенияАсимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее: a — расстояние от центра C до каждой из вершин СоотношенияДля характеристик гиперболы определённых выше подчиняются следующим соотношениям Типы гиперболГиперболу, у которой при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a). Гиперболы, связанные с треугольникомУравненияДекартовы координатыГипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
Канонический видПеремещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
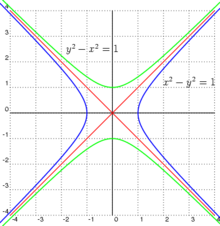
Полярные координатыЕсли полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то Уравнения в параметрической формеВ первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви. СвойстваАсимптотыДля гиперболы, заданной в каноническом виде уравнения двух асимптот имеют вид:
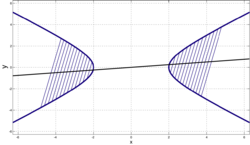
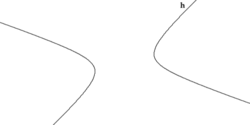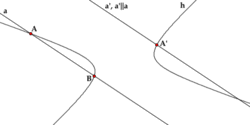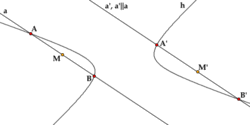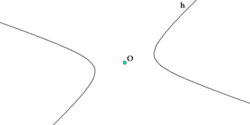
Диаметры и хордыДиаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось. Угловой коэффициент Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси. Касательная и нормальПоскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
или, что то же самое,
Уравнение нормали к гиперболе имеет вид:
Кривизна и эволютаКривизна гиперболы в каждой её точке (x, y) определяется из выражения:
Соответственно, радиус кривизны имеет вид:
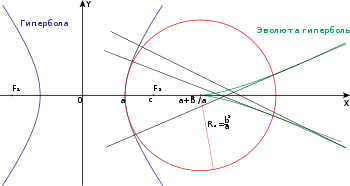
В частности, в точке (a, 0) радиус кривизны равен
Координаты центров кривизны задаются парой уравнений: Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы. ПримененияСм. такжеПримечанияЛитератураЦиклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды) |
 Конические сечения Конические сечения | |
|---|---|
| Главные типы | Эллипс • Гипербола • Парабола |
| Вырожденные | Точка • Прямая • Пара прямых |
| Частный случай эллипса | Окружность |
| Геометрическое построение | Коническое сечение • Шары Данделена |
| См. также | Коническая константа |
| Математика • Геометрия | |
Полезное
Смотреть что такое «Гипербола (математика)» в других словарях:
Гипербола — В Викисловаре есть статья «гипербола» Гипербола (из др. греч … Википедия
Равнобочная гипербола — Гипербола и её фокусы Гипербола геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно, то есть | | F1M | − | F2M | | = C… … Википедия
Эксцентриситет (математика) — Эллипс (e=1/2), парабола (e=1) и гипербола (e=2) с фиксированными фокусом F и директрисой. (|FM| = e |MM |) Эллипс и его e = 1 / 2 Эксцентриситет (обозначается “e” или “ε”) числовая характеристика конического сечения, показывающая степень его… … Википедия
Путь (математика) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
Прямая пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Обратная пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Коническое сечение — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса) … Википедия
Конические сечения — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия












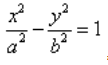
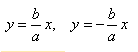
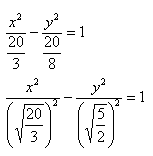
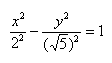
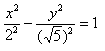
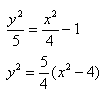
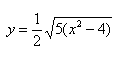
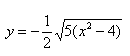

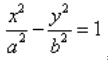
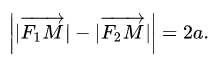
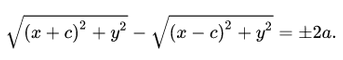
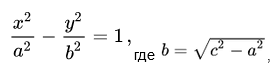

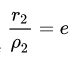
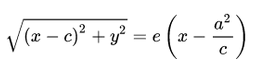
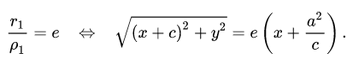
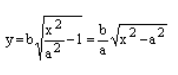

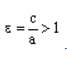


 причем
причем  2a > 0.» border=»0″ />
2a > 0.» border=»0″ />
 1″ border=»0″ /> называется эксцентриситетом гиперболы.
1″ border=»0″ /> называется эксцентриситетом гиперболы.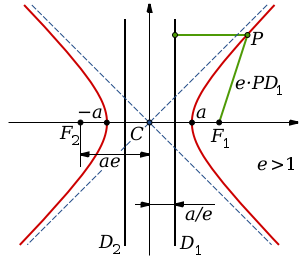
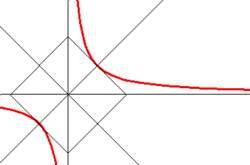
 , называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
 ,
,

 ,
,




 .
.
 параллельных хорд и угловой коэффициент
параллельных хорд и угловой коэффициент  соответствующего диаметра связан соотношением
соответствующего диаметра связан соотношением
 ,
, .
.
 .
. .
.

 .
. .
. .
.
 .
. .
. .
. .
.
 ,
,
 .
.

