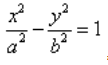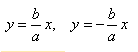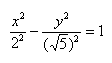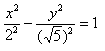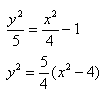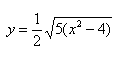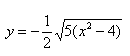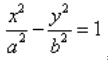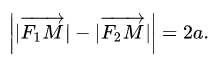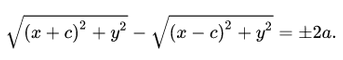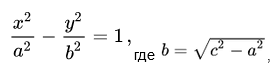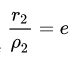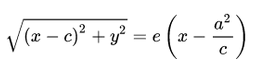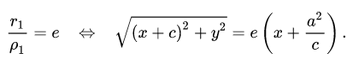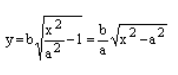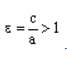Что такое гипербола простыми словами

гипе́рбола

1. матем. плоская кривая, состоящая из двух бесконечных ветвей

2. лингв. стилистическая фигура, состоящая в образном преувеличении какого-либо действия, предмета, явления

3. перен. любое чрезмерное преувеличение

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова летник (существительное):

Источник

Что такое гипербола

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие гиперболы

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:

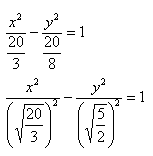
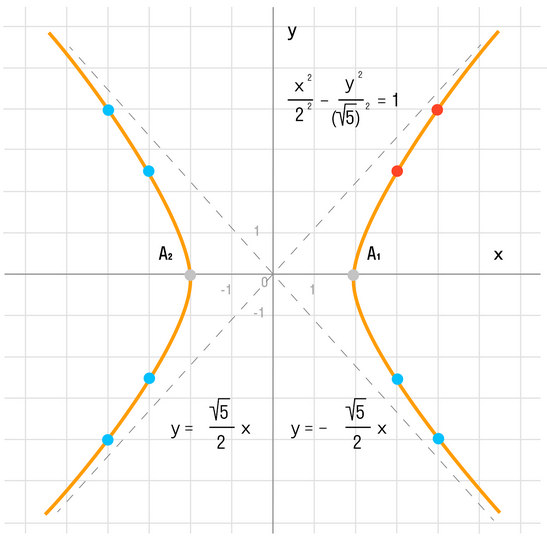
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

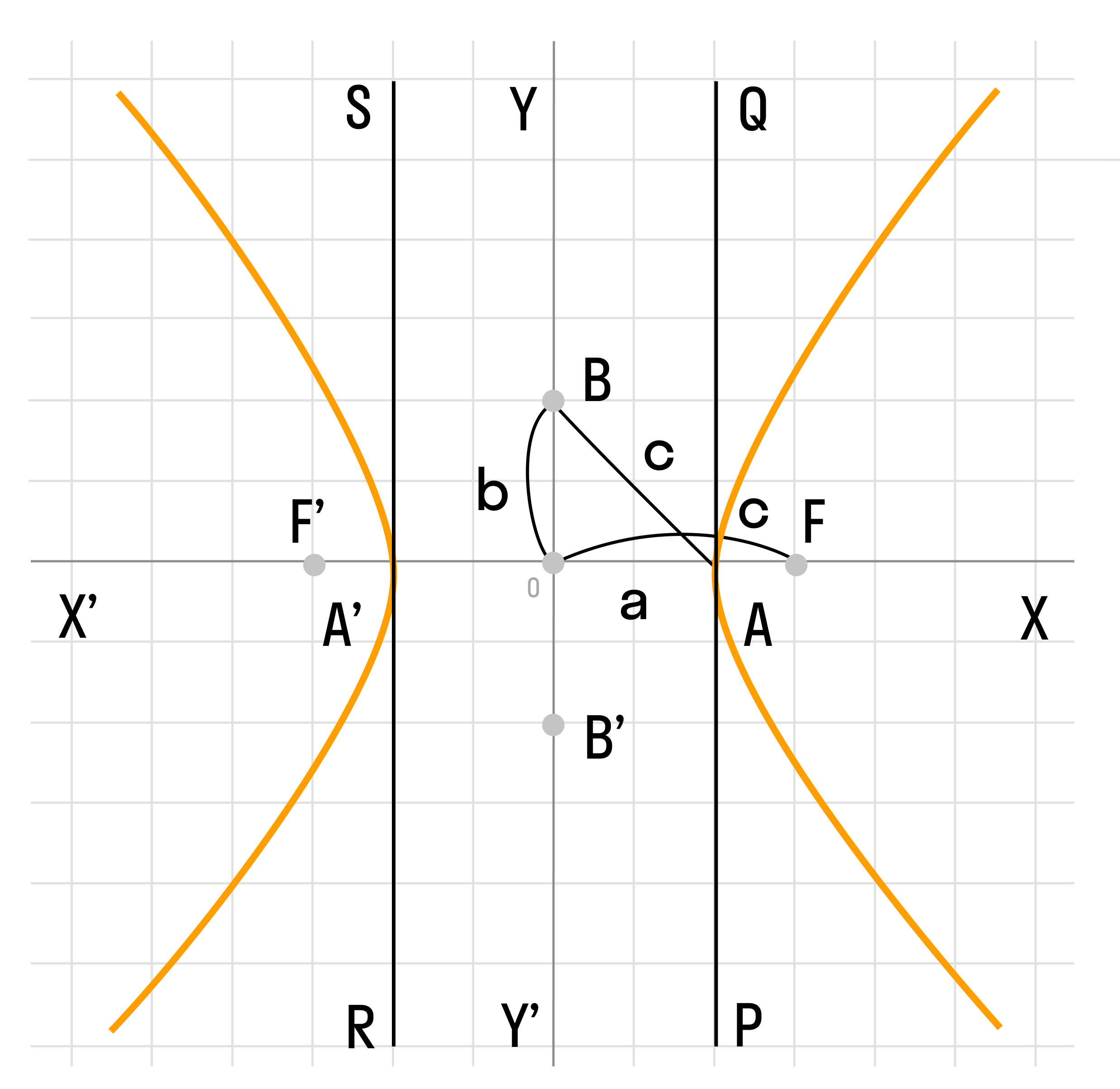
Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Фокальное свойство гиперболы

Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Источник

Что такое гипербола? Примеры

Гипербола — это чрез­мер­ное пре­уве­ли­че­ние каких-либо каче­ствен­ных или коли­че­ствен­ных свойств пред­ме­тов, явле­ний, процессов.

Узнаем, что такое гипер­бо­ла в худо­же­ствен­ной лите­ра­ту­ре, если сна­ча­ла выяс­ним, что это сло­во по сво­е­му про­ис­хож­де­нию явля­ет­ся гре­че­ским: hyperbole — это бук­валь­но зна­чит «пре­уве­ли­че­ние». Начальная часть гипер- явля­ет­ся при­став­кой во мно­гих сло­вах и пере­во­дит­ся как «сверх», «над», «выше нор­мы», напри­мер:

гипер­то­ния, гипер­тро­фия, гиперемия.

Одним из средств уси­ле­ния эмоционально-оценочного и рас­ши­ре­ния смыс­ло­во­го диа­па­зо­на сло­ва, уве­ли­че­ния опо­сред­ствен­но­го отра­же­ния дей­стви­тель­но­сти, образ­но­сти и выра­зи­тель­но­сти речи явля­ют­ся худо­же­ствен­ные тропы:

В худо­же­ствен­ной лите­ра­ту­ре сло­вом «гипер­бо­ла» назы­ва­ют при­ём, состо­я­щий в наме­рен­ном пре­уве­ли­че­нии каких-либо качеств или свойств, явле­ний, про­цес­сов с целью созда­ния ярко­го и впе­чат­ля­ю­ще­го обра­за, например:

В худо­же­ствен­ной лите­ра­ту­ре писа­те­ли при­ме­ня­ют гипер­бо­лу с целью уси­ле­ния выра­зи­тель­но­сти, созда­ния образ­ной харак­те­ри­сти­ки героя, ярко­го и инди­ви­ду­аль­но­го пред­став­ле­ния о нём. С помо­щью гипер­бо­лы выяв­ля­ет­ся автор­ское отно­ше­ние к пер­со­на­жу, созда­ёт­ся общее впе­чат­ле­ние от высказывания.

Примеры использования гиперболы в художественной литературе

И сос­на до звезд доста­ёт. (О. Мандельштам)

Порядочный чело­век от вас за три­де­вять земель убе­жать готов. (Ф.Достоевский)

Миллион тер­за­ний (А.С. Грибоедов «Горе от ума»).

Намеренное пре­уве­ли­че­ние с целью созда­ния гро­тес­ка исполь­зу­ет Н.В. Гоголь в пове­сти «Тарас Бульба»:

К гипер­бо­ле часто при­бе­гал В.В. Маяковский:

Любовь мою, как апо­стол во вре­мя оно, по тыся­че тысяч раз­не­су дорог.

Видеоурок: Гипербола

Источник

Гипербола в русском языке

Всего получено оценок: 100.

Всего получено оценок: 100.

В устной и письменной речи часто используются различные изобразительно-выразительные средства языка. В данной статье кратко рассмотрим, что такое гипербола и каковы ее основные функции, приведем конкретные примеры.

Определение

Гипербола в русском языке – это образное выражение, преувеличение свойств, особенностей предметов и явлений.

Термин «гипербола» греческого происхождения. С греческого «hyperbole» – это преувеличение, излишек.

Преувеличиваться может следующее: значение, сила, чувство, размер, красота.

Гипербола относится к изобразительно-выразительным средствам языка (тропам).

Функции

Гипербола в речи выполняет ряд функций:

Цель преувеличения заключается в том, чтобы усилить выразительность и образность речи.

Примеры

Самыми яркими примерами гипербол являются следующие выражения: бесконечные поляны, быстрый как молния, море слез и др.

Многие гиперболические выражения используются в повседневной жизни. Например: испугаться до смерти, ждать целую вечность, не виделись сто лет, представить тысячу неприятностей, море по колено и др.

Гипербола часто используется в различных художественных произведениях. Приведем примеры из литературы: гора кровавых тел (М. Ю. Лермонтов), пылал во сто сорок солнц (В. В. Маяковский), в муку бы стер вас всех!

Что мы узнали?

Гипербола (с греч. «преувеличение, излишек») – это вид тропа; образное выражение, основанное на преувеличении свойств, особенностей предметов и явлений (значение, сила, чувство, размер, красота и др.). Цель преувеличения: усилить выразительность и образность речи. Гипербола привлекает внимание к высказыванию; обращает внимание на конкретный предмет или явление, на его исключительность; создает комический эффект; выражает авторское отношение к описываемому.

Источник

Что такое гипербола, примеры из литературы и повседневной жизни

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Все мы в жизни хоть раз говорили или слышали подобные выражение (а кто-то и не раз): ВЕЧНО ОПАЗДЫВАЕТЕ или СТО ЛЕТ НЕ ВИДЕЛИСЬ.

И мало кто задумывался, что эти фразы лишены какого-то здравого смысла. Так, человек просто не может «вечно опаздывать». И не может кто-то не видиться «сто лет», хотя бы потому, что люди редко так долго живут.

Подобные преувеличения в русском языке называются гиперболами и именно о них пойдет речь в этой публикации.

Гипербола — это красивое преувеличение

Само это слово греческое – «hyperbole» и обозначает оно «чрезмерность, избыток, преувеличение».

Гипербола – это одно из средств усиления эмоциональной оценки, заключающееся в чрезмерном преувеличении каких-либо явлений, качеств, свойств или процессов. Благодаря этому создается более впечатляющий образ.

Причем часто преувеличение доходит до совершенно непостижимых понятий, иногда даже граничащих с абсурдом. Любой иностранец, если будет переводить такие словосочетания дословно, будет явно озадачен. Мы же давно к ним привыкли, и воспринимаем их как совершенно нормальные.

Вот примеры наиболее часто используемых в обиходе гипербол:

НАПУГАТЬ ДО СМЕРТИ
ТЫСЯЧА ИЗВИНЕНИЙ
ХОТЬ ЗАЛЕЙСЯ
РЕКИ КРОВИ
ГОРЫ ТРУПОВ
ЖДУ ЦЕЛУЮ ВЕЧНОСТЬ
ЕХАТЬ ЗА ТЫСЯЧУ КИЛОМЕТРОВ
ВЕСЬ ДЕНЬ ПРОСТОЯЛА
КУЧА ДЕНЕГ
ПИР НА ВЕСЬ МИР
МОРЕ СЛЕЗ
НЕ ВИДЕЛИСЬ 100 ЛЕТ
ОКЕАН СТРАСТЕЙ
ВЕСИТ СТО ПУДОВ
ЗАДУШИТЬ В ОБЪЯТЬЯХ
ИСПУГАТЬСЯ ДО СМЕРТИ

Все перечисленные выражения мы постоянно используем в разговорной речи. И ради эксперимента просто попробуйте разобрать их дословно и увидите, насколько некоторые из них смешны, а порой и абсурдны.

Ну, например, «хоть залейся» — это должно быть такое количество жидкости, чтобы ее хватило на целый бассейн, в который можно было бы погрузиться с головой. Хотя на самом деле мы этим выражением просто хотим сказать, что напитков у нас много — даже больше чем нужно.

Или фраза «куча денег» на самом ведь деле обозначает просто хорошее финансовое состояние, а не то, что человек собрал все свои сбережения и давай их складывать в одну кучу.

А выражение «ехать за тысячу километров» мы употребляем, ни когда речь идет о реальном расстоянии, например, от Москвы до Волгограда или Ростова-на-Дону. А просто в значении «далеко», хотя на самом деле в реальных цифрах там расстояние может быть всего в несколько километров.

И так можно «развенчать» абсолютно любую гиперболу. Но делать этого не стоит. Они и не должны означать абсолютную правду, их задача – наиболее живописно охарактеризовать конкретную ситуацию или мысль, усиливая ее эмоциональный окрас.

Примеры гипербол в художественной литературе

На самом деле подобные преувеличения – это очень старый литературный прием. Он использовался еще в русских былинах, а это было без малого тысячу лет назад. С помощью гипербол многократно усиливали силу богатырей и их противников.

Сон богатырский длился 12 ДНЕЙ (ну не может человек спать почти две недели)

На пути богатыря стояли силы несметные – ВОЛК ИХ ЗА ДЕНЬ НЕ ОБЕЖИТ, ВОРОН ЗА ДЕНЬ НЕ ОБЛЕТИТ (это сколько врагов должно быть – миллион?)

Махнет богатырь рукой – СРЕДИ ВРАГОВ УЛИЦА, махнет другой – ПЕРЕУЛОК (то есть одним ударом богатырь убивает сразу несколько десятков)

Взял Илья Муромец палицу ВЕСОМ СТО ПУДОВ (тут надо понимать, что сто пудов – это полторы тонны)

Соловей-разбойник свистит – ЛЕС К ЗЕМЛЕ КЛОНИТСЯ, а ЛЮДИ МЕРТВЫМИ ПАДАЮТ (ну тут совсем что-то из разряда сказки)

Точно такие же гиперболы встречаются и в «Слове о полку Игореве». Например:

«Русичи червлеными щитами перегородили широкие поля, ища себе честь, а князю славы» или «Войско такое, что можно Волгу веслами расплескать, а Дон вычерпать шлемами».

Среди писателей больше всего гипербол встречается у Николая Васильевича Гоголя. Преувеличения есть практически в каждом его известном произведении. Вот, например, он описывает реку Днепр:

Редкая птица долетит до середины Днепра.
Днепр как дорога без конца в длину и без меры в ширину.

Или использует преувеличения в своих сатирических произведениях, вкладывая их в уста героев:

В муку бы вас все стер! (Городничий)
Тридцать пять тысяч одних курьеров… Меня сам государственный совет боится. (Хлестаков)

А в «Мертвых душах» есть такие слова: «Бесчисленны человеческие страсти как морские пески».

Гиперболы использует практически любой писатель или поэт. С их помощью они, например, более красочно описывают характер героев произведений или показывают свое авторское отношение к ним.

Причем писатели зачастую не используют уже устоявшиеся выражения, а стараются придумать что-то свое.

Вот еще примеры гипербол в литературе:

Примеры гипербол в рекламе

Конечно, мимо такого интересного приема, который позволяет усилить реальное значение слов, не могли пройти и рекламщики. Масса слоганов основана на этом принципе. Ведь задача – привлечь внимание клиента, обещая при этом «золотые горы» и всячески подчеркивая уникальность товара:

В создании рекламных роликов также часто используется принцип гиперболы. Например, серия знаменитых видео про батончики «Сникерс» со слоганом «Ты не ты, когда голоден». Там, где различные персонажи превращаются в совершенно других людей и начинают творить всякие глупости, и только шоколадный батончик способен вернуть их в привычную русло.

В этих роликах явно гиперболизировано (сильно преувеличено) чувство голода и «чудодейственная» сила самого «Сникерса».

Ну и самый простой пример гипербол, который применяют в рекламе, это выражения типа «самый лучший», «самый стильный», «самый комфортный» и так далее, а про цены, наоборот, говорят «самые низкие».

Вместо заключения

Придать большую выразительность и эмоциональную окраску любому выражению можно не только с помощью гиперболы. Есть в русском языке прием, который является ее полной противоположностью. Он не преувеличивает, а, наоборот, уменьшает значение.

Не успеешь глазом моргнуть, а годы уже пролетели.

Называется такой прием «литота». Об этом подробно – в нашей следующей статье.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Главное слишком не увлекаться. Иначе вашу неудачную гиперболу, могут принять за обычную ложь.

Прочитала статью и поняла, что я любитель всё преувеличивать или преуменьшать. Ведь из гипербол возникают и ложные слухи, даже сплетни. Пусть гипербола останется в литературе, а из нашей устной речи уйдёт, особенно с упоминанием слов «смерть», «испугался», «задушить».

Источник