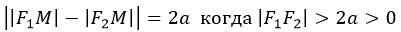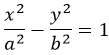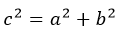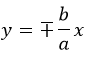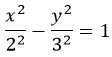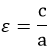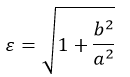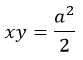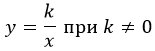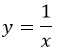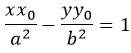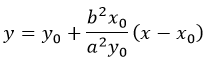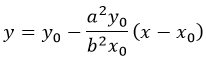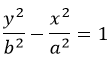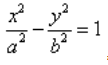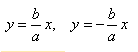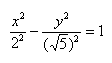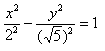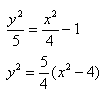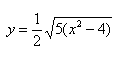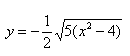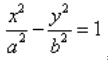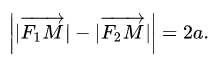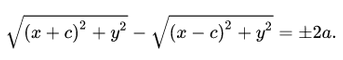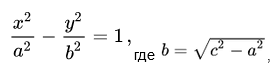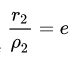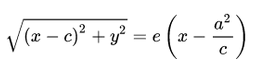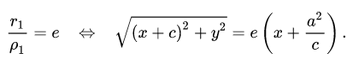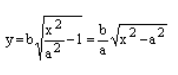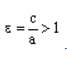Что такое гипербола примеры в математике

Гипербола

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Функция заданная формулой \(y=\frac\), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
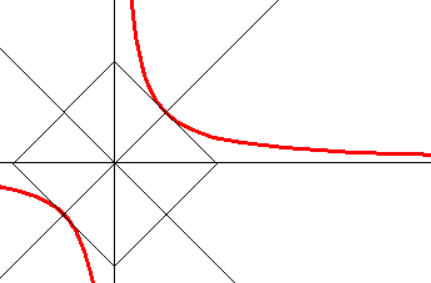
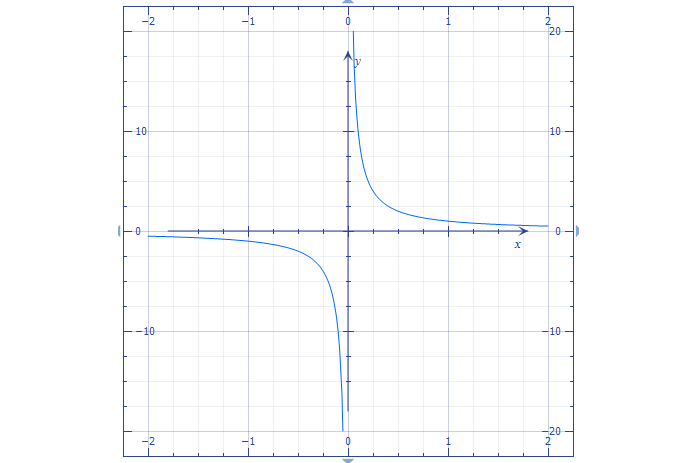
График функции \(y=\frac\) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=\frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment

Источник

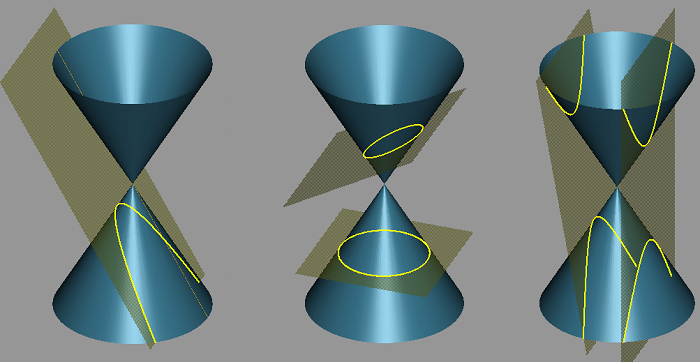
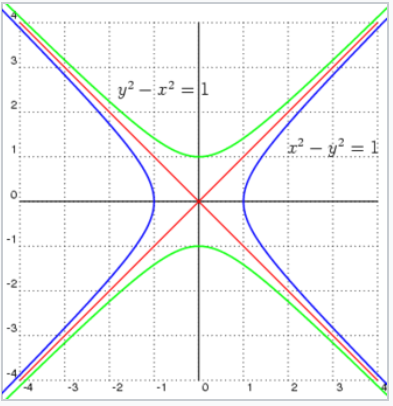
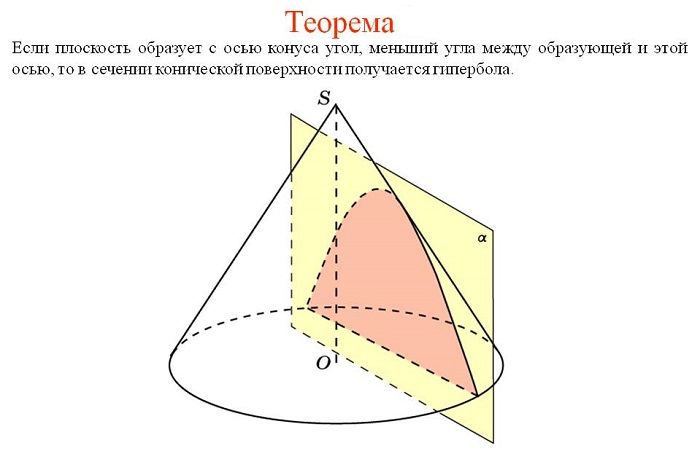
Перед вами родственные кривые, полученные при сечении конуса плоскостью. Парабола, эллипс (окружность), гипербола.

Что такое гипербола в математике

Это геометрическое место точек M, физическая разница расстояний от которых до выбранных (F₁, F₂), называемых фокусами, постоянна.

Оговоримся, что все сказанное относится к Евклидовой плоскости, где параллельные прямые не пересекаются.

Но если из отрезка |F₁F₂| соорудить координатную прямую X, за начальную точку взять середину (она же будет центром гиперболы) отрезка, то получим декартову систему координат. Где кривая описывается алгебраическим уравнением II-го порядка.

Получим классическую формулу аналитической геометрии:

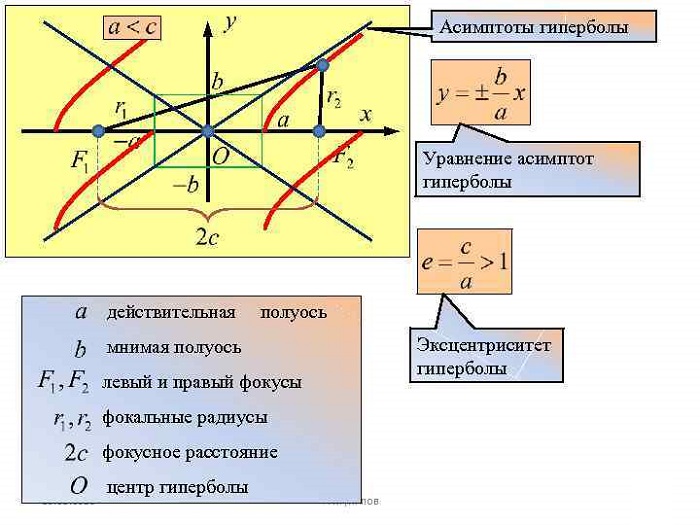
где a – действительная полуось, b – мнимая.

поскольку x и y связаны квадратной зависимостью, обе оси будут осями симметрии;

пересечения с осью абсцисс (фокусов) с координатами ±a называются вершинами гиперболы, и расстояние между ними является минимальной дистанцией между ветвями (о последних ниже);

кратчайший отрезок от фокуса до вершины зовется перицентрическим расстоянием и пишется «r_p».

Асимптоты и фокусы гиперболы

Фокусы находятся на оси X (из этого исходили). Расстояние до центра гиперболы (он же центр симметрии C) называется фокальным и обозначается «c». Его формула:

Умозрительно очевидно, что сечение конуса состоит из двух кривых. Называются они ветвями гиперболы. Также не подлежит сомнению то, что ветви ограничены воображаемой поверхностью. Фокусы всегда находятся внутри ветвей.

Помучившись с производными и пределами, получим формулы асимптот (прямые, расстояние до которых от кривой стремится к нулю на бесконечном удалении от «0»):

Дистанцию от фокуса до асимптоты зовут прицельным параметром и обозначают буквой «b».

Как построить график функции гиперболы

Существует много ресурсов, где можно онлайн наблюдать, как строится функция. Но нужно все уметь самому. Итак, давайте учиться.

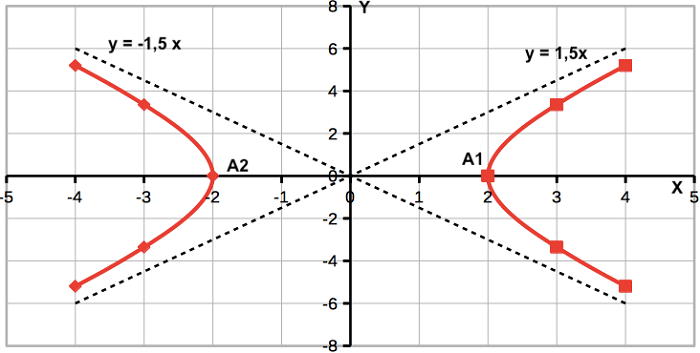
Построим для примера график уравнения

По формуле выше выстраиваем асимптоты.

Отмечаем вершины х = ±2 (А1, А2). Приблизительный вид уже ясен.

При х = ±3, y = ±3,5 (примерно).

Эксцентриситет гиперболы

Эксцентриситетом считают величину:

Является параметром, характеризующим отклонение конического сечения от окружности:

кривые с равным эксцентриситетом подобны;

показатель угла наклона асимптот.

Равнобочная (равносторонняя) гипербола

Таковой кривая является при условии a = b. Если покрутить систему координат, функцию можно свести к виду:

Эксцентриситет данной конструкции составит квадратный корень из 2.

Иначе говоря, получаем график обратной пропорциональности:

Или «любимую» школьниками.

Коль уж речь зашла о школьном курсе, добавим сведений:

прямые x = 0, y = 0 – асимптоты;

область определения – все действительные числа, кроме 0;

область значений – все, за исключением 0;

функция нечетная, поскольку меняет знак при смене знака аргумента;

убывающая при положительных и отрицательных x.

Касательная и нормаль

В каждой точке гладкой кривой возможно построить касательную и нормаль (перпендикуляр). Гипербола – не исключение. Касательная – прямая, совпадающая с кривой только в одной точке (в пределах изгиба одного порядка).

Уравнение касательной в точке с координатами (x₀y₀) имеет вид:

Сопряженные гиперболы

Записанное таким образом уравнение даст сопряженную фигуру:

То есть с теми же асимптотами, но расположенную по-другому, с поворотом на 90°.

Свойства гиперболы

Их должен знать каждый школьник:

Касательная в произвольной точке H окажется биссектрисой угла F₁HF₂.

Кривая симметрична относительно осей и своего центра.

Отсеченный асимптотами отрезок касательной делится точкой соприкосновения пополам. Площадь же выделенного треугольника не меняется от изменения точки.

Использование

Где применяются знания о гиперболе:

для создания эллиптических и других координат;

в солнечных часах (сечение конуса света);

для анализа движения космических объектов.

Заключение

Непростая кривая с неожиданными в некоторых случаях применением. Что удивительно, задача о сечениях конуса была поставлена древнегреческими учеными во II-м веке до нашей эры. Это говорит о высочайшем уровне тогдашних инженеров.

Нет, солнечные часы понятно были, а мелких искусственных спутников не было точно. И астероиды не исследовали, но вопросы возникали. И были ответы без ссылок на многочисленных богов. Удивительные люди.

Источник

Что такое гипербола

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие гиперболы

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

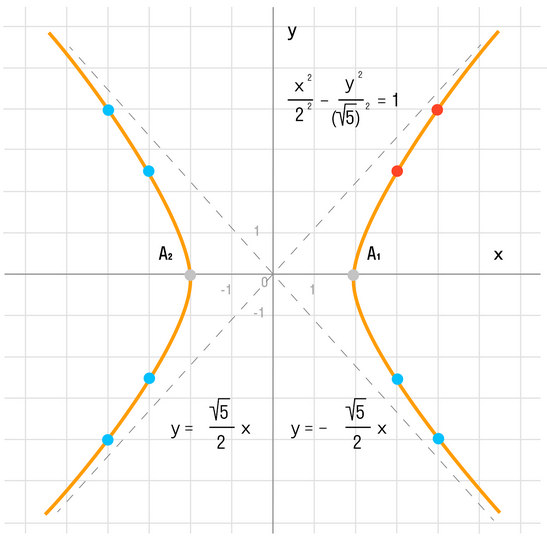
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:

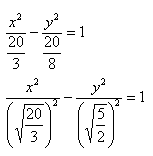
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

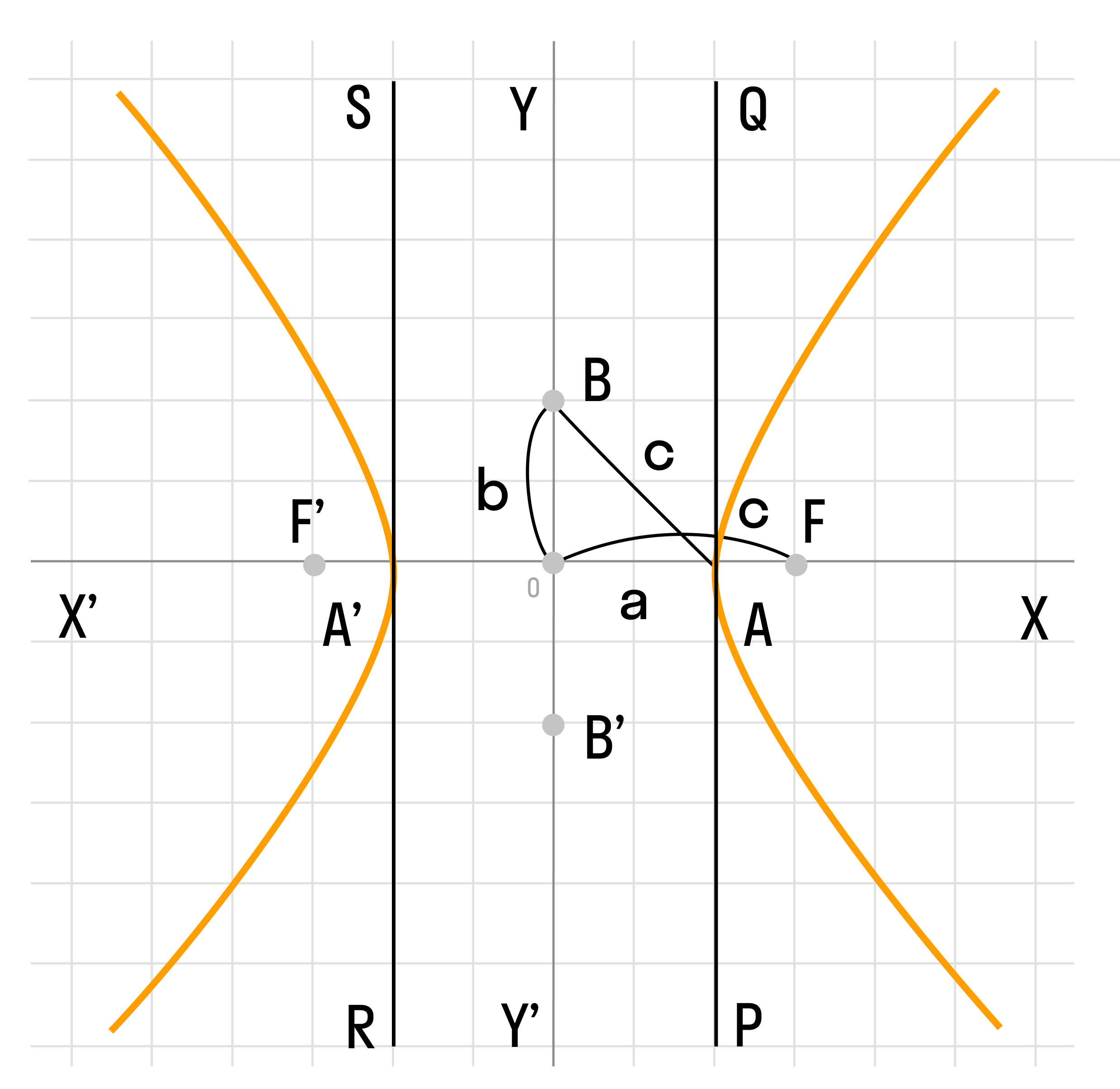
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Фокальное свойство гиперболы

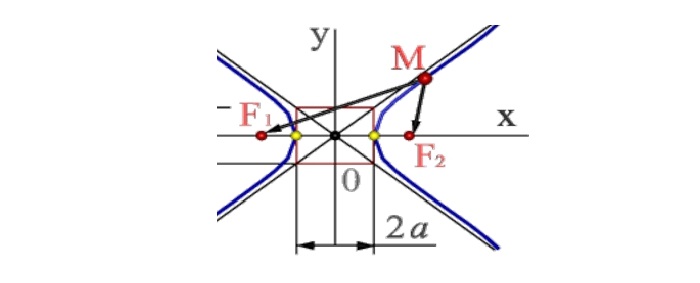
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Источник

Гипербола: определение, функция, формула, примеры построения

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

Пример 1

Дана функция y = 4 /_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

0,5

8

1

4

2

2

4

1

8

0,5

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y. Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено. Пример 2 Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже: Источник ← Что такое гипербола пример Что такое гипербола примеры → Вам также понравится Что такое бизнес логика в программировании 17.04.202223.04.2022 admin 0 Что можно посмотреть в пермском крае на машине 16.04.202218.04.2022 admin 0 Что такое градиент давления в скважине 17.04.202227.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.