Что такое гипербола определение
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| 0,5 | 8 | 1 | 4 | 2 | 2 | 4 | 1 | 8 | 0,5 | fpm_start("true"); Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y. Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено. Пример 2Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже: Значение слова «гипербола»[От греч. ‛υπερβολή — преувеличение] [От греч. ‛υπερβάλλω — прохожу через что-л.] Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека Гипербола (математика) — плоская кривая второго порядка. Гипербола (риторика) — троп, преувеличение. ГИПЕ’РБОЛА, ы, ж. [греч. hyperbolē]. 1. Кривая из числа конических сечений (мат.). Г. получается при сечении прямого круговорота 2. Фигура преувеличения (лит.). Стиль Гоголя изобилует гиперболами. || Всякое чрезмерное, преувеличенное высказывание по поводу чего-н. (книжн.). Ну, это г.: в действительности всё происходило проще. Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека гипе́рбола1. матем. плоская кривая, состоящая из двух бесконечных ветвей 2. лингв. стилистическая фигура, состоящая в образном преувеличении какого-либо действия, предмета, явления 3. перен. любое чрезмерное преувеличение Делаем Карту слов лучше вместе Спасибо! Я стал чуточку лучше понимать мир эмоций. Вопрос: умудрённость — это что-то нейтральное, положительное или отрицательное? Гипербола (математика) Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы. СодержаниеИсторияТермин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком. ОпределенияГипербола может быть определена несколькими путями. Коническое сечениеГипербола может быть определена, как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами. Как геометрическое место точекЧерез фокусыГипербола может быть определена, как Геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна. Для сравнения: кривая постоянной суммы расстояний между двумя точками — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини. Через директрису и фокусГеометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная Связанные определенияАсимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее: a — расстояние от центра C до каждой из вершин СоотношенияДля характеристик гиперболы определённых выше подчиняются следующим соотношениям Типы гиперболГиперболу, у которой при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a). Гиперболы, связанные с треугольникомУравненияДекартовы координатыГипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
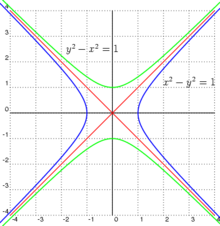
Канонический видПеремещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду
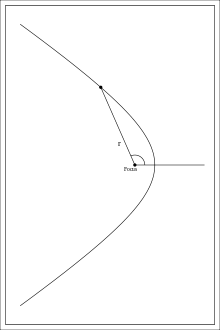
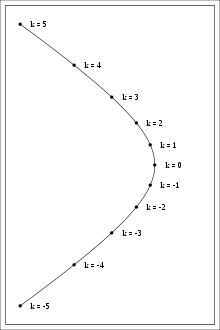
Полярные координатыЕсли полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то Уравнения в параметрической формеВ первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви. СвойстваАсимптотыДля гиперболы, заданной в каноническом виде уравнения двух асимптот имеют вид:
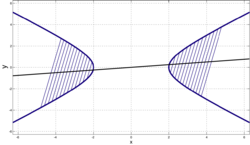
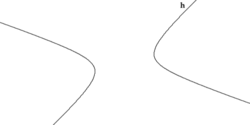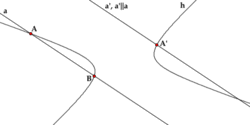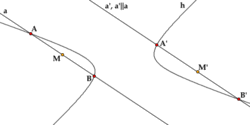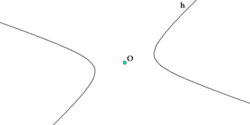
Диаметры и хордыДиаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось. Угловой коэффициент Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси. Касательная и нормальПоскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
или, что то же самое,
Уравнение нормали к гиперболе имеет вид:
Кривизна и эволютаКривизна гиперболы в каждой её точке (x, y) определяется из выражения:
Соответственно, радиус кривизны имеет вид:
В частности, в точке (a, 0) радиус кривизны равен
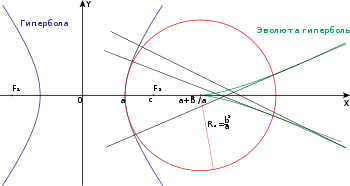
Координаты центров кривизны задаются парой уравнений: Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы. ПримененияСм. такжеПримечанияЛитератураЦиклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды) |
 Конические сечения Конические сечения | |
|---|---|
| Главные типы | Эллипс • Гипербола • Парабола |
| Вырожденные | Точка • Прямая • Пара прямых |
| Частный случай эллипса | Окружность |
| Геометрическое построение | Коническое сечение • Шары Данделена |
| См. также | Коническая константа |
| Математика • Геометрия | |
Полезное
Смотреть что такое «Гипербола (математика)» в других словарях:
Гипербола — В Викисловаре есть статья «гипербола» Гипербола (из др. греч … Википедия
Равнобочная гипербола — Гипербола и её фокусы Гипербола геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно, то есть | | F1M | − | F2M | | = C… … Википедия
Эксцентриситет (математика) — Эллипс (e=1/2), парабола (e=1) и гипербола (e=2) с фиксированными фокусом F и директрисой. (|FM| = e |MM |) Эллипс и его e = 1 / 2 Эксцентриситет (обозначается “e” или “ε”) числовая характеристика конического сечения, показывающая степень его… … Википедия
Путь (математика) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
Прямая пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Обратная пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Коническое сечение — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса) … Википедия
Конические сечения — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия




 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!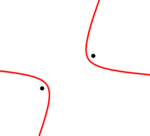


 причем
причем  2a > 0.» border=»0″ />
2a > 0.» border=»0″ />
 1″ border=»0″ /> называется эксцентриситетом гиперболы.
1″ border=»0″ /> называется эксцентриситетом гиперболы.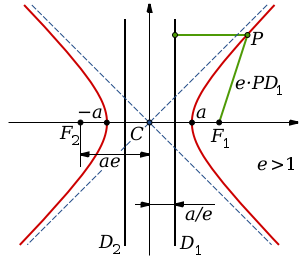
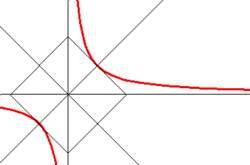
 , называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
 ,
,

 ,
,




 .
.
 параллельных хорд и угловой коэффициент
параллельных хорд и угловой коэффициент  соответствующего диаметра связан соотношением
соответствующего диаметра связан соотношением
 ,
, .
.
 .
. .
.

 .
. .
. .
.
 .
. .
. .
. .
.
 ,
,
 .
.

