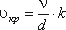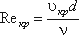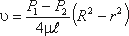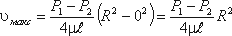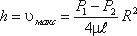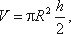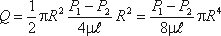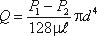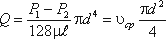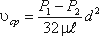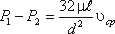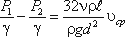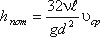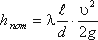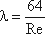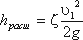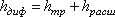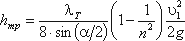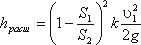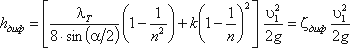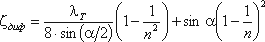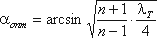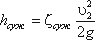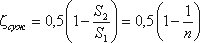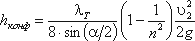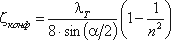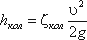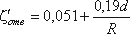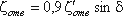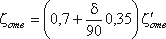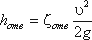Что такое гидравлические потери

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Содержание статьи

Коэффициент гидравлического сопротивления

Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:

где ρ — плотность среды, g — ускорение свободного падения.

В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.

где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

Значение коэффициента ξ_{вн. суж} от значения отношения (F₂/F₁)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле

ξ _{поворот} = 0,946sin(α/2) + 2.047sin(α/2) 2

где α – угол поворота трубопровода.

Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:

ξ_вх = 0,505 + 0,303sin α + 0,223 sin α 2

Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

Гидравлическое сопротивление полностью открытой запорной арматуры равно

ξ_{вентиля} = от 2,9 до 4,5

Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.

Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.

Для диафрагмы с острыми краями:

Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

Видео о гидравлическом сопротивлении

На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)

Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.

Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

Источник

Гидравлические потери

Гидравлические потери принято разделять на два вида:

Гидравлические потери выражают либо в потерях напора в линейных единицах столба среды, либо в единицах давления : , где — плотность среды, g — ускорение свободного падения.

Содержание

Коэффициенты потерь

Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха [2]

,

;

таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζ_тр=λL/d.

Влияние режима течения в трубах на гидравлические потери

Значение в технике

На преодоление гидравлических потерь в различных технических системах затрачивается работа таких устройств, как насосы, воздуходувки.

Для уменьшения гидравлических потерь рекомендуется в конструкциях гидроборудования избегать применения деталей, способствующих резкому изменению направления потока — например, заменять внезапное расширение трубы постепенным расширением (диффузор), придавать телам, движущимся в жидкостях, обтекаемую форму и др. Даже в абсолютно гладких трубах имеются гидравлические потери [2] ; при ламинарном режиме шероховатость мало на них влияет, однако при обычных в технике турбулентных режимах её увеличение, как правило, вызывает рост гидродинамического сопротивления.

Иногда, напротив, требуется ввести гидравлическое сопротивление в поток. Для этого применяются дроссельные шайбы, редукционные установки, регулирующие клапана. По измерению давления на некотором элементе, график коэффициента гидравлического сопротивления которого известен, можно узнать скорость потока в некоторых распространённых типах расходомеров.

Источник

Что такое потери напора?

Третья статья в цикле статей по теоретическим основам гидравлики посвящена определению потерь напора.

Как рассказывалось ранее, при своем движении жидкость испытывает сопротивление, что выражается затратами ее энергии, т.е. затратами ее напора, что называют потерями напора.

Два вида потерь напора

Потери напора принципиально делятся на два типа:

Местные потери конкретно на данном рисунке: поворот, задвижка (условное обозначение по ГОСТ – «бантик»), еще один поворот и внезапное (т.е. не плавное) расширение.

Местные потери

Местные потери напора (говорят также “потери напора на местные сопротивления“) – это потери напора, которые происходят в основном из-за вихреобразования в конкретных местах трубопровода (потому и «местные»). Любое препятствие на пути движения потока жидкости является местным сопротивление. Чем сильнее деформируется поток, тем больше будет потеря напора. Например, на рисунке ниже показано внезапное сужение трубопровода. Хорошо видны 4 вихревые зоны до и после сужения.

Местную потерю напора можно определить, зная коэффициент сопротивления для данного сопротивления (обозначается буквой дзэта ζ, не имеет размерности) и среднюю скорость потока в сопротивлении V.

Пример. Определить потерю напора в вентиле, установленном на трубе внутренним диаметром d = 51 мм, при расходе Q = 2 л/с.

Сначала по уравнению неразрывности (ссылка на статью 2) определим среднюю скорость движения жидкости.

V = Q / ω = 4 · Q / 3,14 · d² = 4 · 0,002 / 3,14 · 0,051² = 0,98 м/с

Теперь необходим коэффициент сопротивления вентиля. Такие данные берут из гидравлических справочников или у производителей конкретной арматуры. По справочным данным находим, что коэффициент местного сопротивления вентиля равен 6.

Тогда потеря напора на вентиле: h_вент = ζ · V²/ 2 · g = 6 · 0,98² / 2 · 10 = 0,29 м.

Иллюстрация местных потерь напора

При расчете трубопроводных систем (внутренний водопровод здания, наружная водопроводная сеть и т.п.) обычно высчитывают не все сопротивления (так как их может быть очень много), а только самые существенные, создающие наибольшие сопротивления: например, счетчик воды. Потеря напора на остальных местных сопротивлениях учитывается коэффициентом, на который умножается значение потерь напора по длине (1,05 – 1,15 для наружных сетей, 1,1 – 1,3 для внутренних сетей здания).

Потери по длине

Потери напора по длине – потери напора на участках трубопровода. Возникают из-за работы сил трения. (сила трения возникает между слоями движущейся жидкости). Величина потерь напора, также, как и местных потерь, напрямую зависит от скорости движения жидкости. При достаточно высокой скорости усиливается влияние шероховатости стенок трубы.

Потерю напора по длине можно увидеть по разнице в уровнях воды между двумя пьезометрами

Точное определение потерь напора по длине является довольно сложной задачей, для этого необходимо устанавливать режим движения жидкости (бывает ламинарный и турбулентный), подбирать расчетную формулу для коэффициента гидравлического трения в зависимости от числа Рейнольдса Re, характеризующего степень турбулизации потока. Это изучается студентами в рамках курса механики жидкости.

При этом для быстрого расчета потерь напора были составлены специальные таблицы для инженеров, позволяющие, зная материал трубы и ее диаметр, а также расход воды, быстро определить так называемые удельные потери напора (сколько напора теряется на 1 м трубы). Эта величина называется 1000i, значение 1000i = 254 означает, что поток, проходя 1 м такой трубы теряет 254 мм (миллиметра) напора, т.е. 0,254 метра. Это значение также называется «гидравлический уклон», и это нельзя путать с геодезическим, т.е. просто с физическим уклоном (наклоном) самой трубы. Для расчета стальных труб используют таблицы Шевелева.

Скачать таблицы таблицы Шевелева в формате PDF можно на нашем сайте.

Таблицы Шевелева для определения потерь напора

Например, из данного фрагмента видно, что если вода с расходом 1,50 л/с пойдет по трубе диаметром 50 мм, то скорость в этой трубе будет 0,47 м/с, а 1000i составит 9,69 мм на метр (на каждом метре трубы теряется 9,69 миллиметров напора).

Чтобы определить, сколько метров напора будет потеряно на всем участке – нужно перемножить 1000i с длиной участка. Чтобы ответ получился в метрах, 1000i делят на 1000.

Итак, потери напора по длине: h_l = 1000i·l / 1000 = i·l

Если наш участок трубы имеет длину, скажем, 25 метров, то потеря напора на нем:

h_l = 9,69*25/1000 = 0,24 м.

Учтем и местные сопротивления, тогда полная потеря напора на данном участке:

Таблицы были переведены в электронный вид в виде программы, созданной Любчуком Ю.Е.
Загрузить программу “Таблицы Шевелева” можно с нашего сайта.

С помощью этой программы, можно легко посчитать потери напора в трубах из различных материалов. В следующей статье подробно опишем, как пользоваться данной программой на задаче из жизни.

Источник

Что такое гидравлические потери

Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

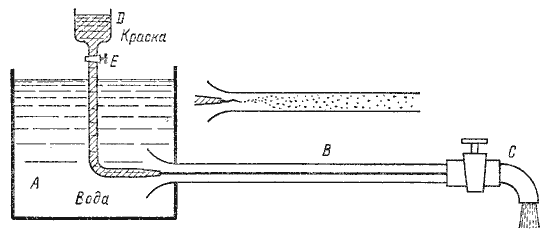
Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.

Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ _кр.

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

Как показывает опыт, для труб круглого сечения Re_кр примерно равно 2300.

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.

В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.

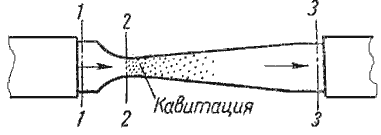
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.

При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.

Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.

При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.

Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.

Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.

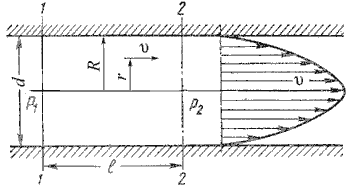
Уравнение, связывающее переменные υ и r, имеет следующий вид:

Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.

Максимальная скорость дает высоту параболоида

Как известно из геометрии, объем параболоида высотой h и площадью ρR 2 равен

Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид

Расход в трубе можно выразить через среднюю скорость:

Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).

Потеря давления в трубопроводе будет равна

Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

Так как левая часть полученного равенства равна потерям напора h_пот в трубе постоянного диаметра, то окончательно это равенство примет вид:

Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:

Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re 2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

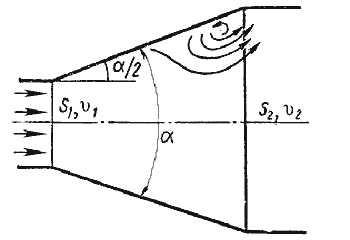
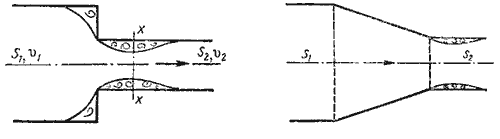
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

Учитывая это полную потерю напора можно переписать в виде:

откуда коэффициент сопротивления диффузора можно выразить формулой

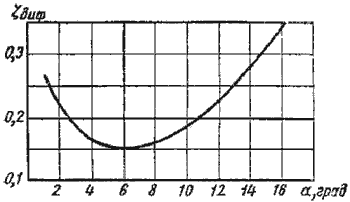
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рис.4.11).

3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).

Полная потеря напора определится по формуле ;

где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

где коэффициент сопротивления конфузора определяется по формуле

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).

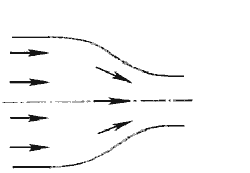
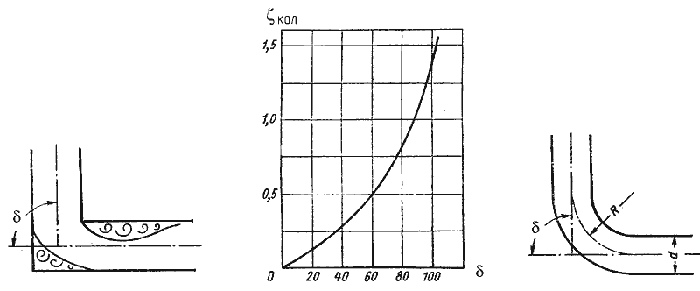
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.

Источник