Что такое геометрический рисунок
Геометрический орнамент
Становление геометрического орнамента
Геометрически орнамент возник задолго до появления текстиля, керамики, металлических предметов быта и орудий труда и каких бы то ни было рукотворных архитектурных сооружений. Как украшения для этих форм он стал использоваться по мере их изобретения. В большинстве случаев орнамент при этом выполнял не столько функцию украшения, сколько нес сакральный мистический смысл. Одним из самых первых распространившихся повсеместно элементов орнамента стал ромб. Так же достаточно часто использовался ромбо-меандровый орнамент. Данный геометрический элемент можно считать структурообразующим. Именно ромб лежит в основе орнамента в целом.
В качестве примера можно привести найденные на территории России костяные фигурки Матери-прародительницы, относимые к эпохе палеолита, декорированными именно ромбическим орнаментом. Женщины того времени на празднествах украшали себя именно таким узором. Постепенно он стал символом именно плодородия, удачи и процветания. Палеонтологом В. И. Бибиковой было убедительно доказано, что ромб и волнообразные линии, часто сопровождающие его, являются ничем иным, как воспроизведением узора мамонтовой кости. Раскопки показали, что такой орнамент использовался повсеместно, начиная от неолита и до бронзового века. Вплоть до гальштатской эпохи он помещался в основном на ритуальных предметах и жертвенниках.
Во время неолита к ромбо-меандровому орнаменту добавляются спирально-змеиный и линейно-струйчатый. Для этого периода характерны вертикальные линии, волнистые либо прямые, символизирующие дождь. Часто композицию дополняли клубки сплетшихся змей. Важным этапом в становлении орнамента считается возникновение геоцентрической идеи. Именно она стала символом завершения человеком познания мира. Изображения коловрата встречаются, например, на русских прялках, прославянских сосудах, в русских народных костюмах и т.д. Чаще всего «колесо Юпитера» изображалось с шестью спицами. Широко использовался этот орнаментальный элемент и в резьбе. В данном случае он носил название «громового знака». Все основные виды геометрического орнамента полностью сложились уже к I в до н. э. За прошедшие столетия этот вид декора изменений практически не претерпел. Если сравнить, например, орнаменты фабричных тканей XVIII – XX века с древними декорами, особой разницы заметить нельзя.
Арабский геометрический орнамент
В историю арабский геометрический орнамент вошел под названием «гирих» (араб. – «узел»). Мотивом восточного декора часто становилась плотно связанная орнаментальная сетка. В основе гириха лежит разделенный на части круг. Таким образом, происходит построение всех других фигур – треугольника, прямоугольника, многоугольника и т.д. Такое композиционное решение позволяет создавать симметричные мотивы. Любой геометрический орнамент всегда математически правилен и может быть разделен на равные части. Особенностью арабского гириха является некоторый отход от этой точности, предоставляющей художнику больший простор для творчества.
Создание бесконечного орнамента состоит из следующих основных этапов:
• выбор определений раппортной системы;
• построение отдельных мотивов;
• размещение их на сетке;
• выбор способа исполнения (зависит от материала).
Художественная сторона в орнаментах напрямую связана с четвертым этапом, то есть находиться в полностью зависимости от того, на каком предмете будет выполняться декор. Еще одной особенностью именно арабского узора является получения очень сложных геометрических систем всего лишь из одного мотива. О сложности орнаментов говорит, например, то, что уже в XVIII веке восточные художники умели гармонично сочетать двенадцатиконечные звезды с пятиконечными.
Рисование геометрических тел
Изучение и рисование геометрических тел в учебном академическом рисунке является основой для освоения принципов и методов изображения более сложных форм.
Обучение изобразительным искусствам требует строгого соблюдения последовательности усложнения учебных задач и многократных повторений для овладения техникой. Наиболее подходящей формой для усвоения принципов построения рисунка являются геометрические тела, имеющие в своей основе ясные конструктивные строения. На простых геометрических телах легче всего понять и усвоить основы объемно-пространственной конструкции, передачи форм в перспективном сокращении, закономерности светотеней и пропорциональные отношения.
Упражнения по рисованию простых геометрических тел позволяют не отвлекаться на детали, имеющиеся в более сложных формах, таких, как архитектурные объекты и тело человека, а всецело сосредоточиться на главном — изобразительной грамоте.
Правильно понятые и усвоенные закономерности при изображении простых форм должны способствовать более осознанному подходу к рисованию сложных форм в последующем.
Для того чтобы научиться грамотно и правильно изображать форму предмета, необходимо осознать скрытую от глаз внутреннюю структуру предмета — конструкцию. Под словом «конструкция» (от латинского construct) подразумевается «строение», «структура», «план», то есть взаимное расположение частей предмета и их соотношение. Это важно знать и понимать при изображении любых форм. Чем сложнее форма (независимо от материала, фактуры и цвета предмета), тем больше и серьезнее студентам придется изучать внутреннее строение натурной модели. Гак, например, при рисовании живой натуры — головы или фигуры человека, помимо знания общеконструктивных особенностей непременно следует знать и пластическую анатомию. Поэтому без ясного понимания строения формы и характера предмета невозможно грамотно освоить рисунок.
При изображении пространственных форм, кроме знания закономерностей строения конструкции, необходимы знания о законах перспективы, пропорции, светотени. Вопросы, касающиеся перспективы и пропорции, подробно освещены в разделах «Пропорции» и «Основы перспективы».
Для правильного изображения натурной модели студентам необходимо еще раз напомнить о необходимости приучить себя всегда анализировать натуру, ясно представлять ее внешнее и внутреннее строение. К сожалению, как показывает практика, многие студенты ограничиваются лишь поверхностным впечатлением, не углубляясь в суть строения формы предмета. В искусстве, как и в любой науке, к изучению натурного предмета необходимо подходить с научной точки зрения. Подходить к работе следует осознанно, не довольствуясь копированием внешних форм, которые видит глаз. Такое рисование не будет способствовать успешному выполнению работ по изображению как простых, так и сложных форм.
Рисование геометрических форм малоопытным рисовальщикам кажется на первый взгляд достаточно легким. Но это далеко не так. Не имея достаточного опыта в рисовании, студенты легко привыкают к механическому копированию. Поэтому при изображении более сложных форм можно легко запутаться. Для более уверенного овладения рисунком прежде всего необходимо освоить методы анализа форм и принципы геометрического построения простых тел.
Любая форма состоит из плоских фигур: прямоугольников, треугольников, ромбов, трапеций и других многоугольников, которые отграничивают ее от окружающего пространства. Задача заключается в том, чтобы правильно понять, как эти поверхности сочетаются между собой, образуя форму. Для правильного ее изображения студентам необходимо научиться рисовать такие фигуры в перспективе, чтобы без особого труда выделять на плоскости объемные тела, ограниченные этими плоскими фигурами. Плоские геометрические фигуры служат основой понимания конструктивного построения объемных тел. Так, например, квадрат дает представление о построении куба, прямоугольник — о построении призмы параллелепипеда, треугольник — пирамиды, трапеция — усеченного конуса, круг представляется шаром, цилиндром и конусом, а эллипсовидные фигуры — шарообразными (яйцевидными) формами (рис.34).
Рисунки геометрических фигур карандашом с перспективой, тенью поэтапно на плоскости
Простейшие геометрические фигуры карандашом – начальная стадия рисования любого объекта. Об этом свидетельствует компьютерное моделирование. Как и компьютерные трехмерные объекты включают в себя множество фигур, изображение делится на формы.
Особенности построения геометрических фигур
Рисунок геометрических фигур карандашом имеет такие этапы:
| № | Этап | Описание |
| 1 | Анализ модели | Необходимо представить фигуру как каркас из точек и линий. Прорисовывание невидимых линий – главный методологический прием, помогающий рисовать сложные модели. |
| 2 | Наметка линий и вершин | Для этого нужно совершать легкие скользящие движения карандашом, не надавливая на него слишком сильно. |
| 3 | Обозначение видимых ребер | Следует детально прорисовать линии, которые видимы зрителю. Например, если изображается шар или конус, то детально прорисовываются края формы. |
| 4 | Штриховка | С ее помощью можно отобразить расположение теней. |
Штриховка
Штриховка – важный элемент в изображении трехмерных объектов. С ее помощью художник передает тень.
Правила, которые следует запомнить начинающему творцу, следующие:
Свет и тень
Любая тень образуется, если имеется источник света. Художник должен заранее определить, где именно располагается этот источник и с какой стороны падают на предмет лучи. Если при рисовании возникают трудности со светотенью, следует потренироваться на простом варианте.
Применять можно одну из 2-х техник – штриховку или растушевку. Перед работой рекомендуется включить свет, который будет направлен на предмет. Также важно, чтобы в помещении не было других, более ярких источников света.
Начинающий художник должен запомнить, что существуют следующие участки на рисунке:
| Участок | Описание |
| Блик | Часть рисунка, отражающая свет лампы или солнечного луча. |
| Свет | Области, освещенные лучами под прямым углом. |
| Полутень | Области, располагающиеся между светом и тенью. Их еще называют промежуточными. |
| Тень | Это не освещенные области. |
| Рефлекс | Это освещаемый участок, который получается от предметов поблизости. Огромную роль играет яркость падающего света: чем он ярче, тем более насыщенной будет тень. |
| Падающая тень | Тень от фигуры на то, что находится вокруг. Например, на горизонтальную поверхность, где располагается фигура или стена возле нее. |
Важно уметь находить границу между светом и тенью. Ее форма зависима от рисуемого изображения. К примеру, на шаре эта граница одна, а на кубе – другая. Проблема поиска границы заключена в том, что она обычно размытая. Изредка она бывает четкой: чем ярче свет, тем четче граница.
Например:
В изобразительном искусстве применяется прием, носящий название – «кьяроскуро». Он основан на противопоставлении освещенной и затененной областей. При искусственном освещении образуется среда, где свет становится слишком ярким, а тень – очень темной, что придает насыщенности и резкости.
Рисование в перспективе: куб
Рисунок геометрических фигур карандашом следует начинать с куба.
Обычно применяется белая гипсовая модель, на которой отчетливо видна светотень. Модель лучше приобрести или сделать самостоятельно, фотографию использовать не рекомендуется.
Для изображения необходимо:
Рисование геометрических тел вращения
Геометрические тела вращения начинают рисовать только после освоения изображения куба. Изначально фигуры изображают по отдельности, после – пробуют натюрморт.
Для успеха прорисовывания сложных форм, начинают с изображения простых. Модели можно приобрести в магазине или изготовить своими силами. Для этого используется картон или толстая бумага.
Фигуры нельзя заменять их фотографиями: срисовывание объемных фигур с плоской поверхности лишено смысла и не несет пользы.
Конус
Слово «конус» имеет греческое происхождение. Оно переводится как «сосновая шишка». Такое название фигуре дали потому, что она похожа на шишку или на колпак.
Если же выражаться математическим языком, эта фигура является симметричным телом, которое образуется вследствие объединения лучей, берущих начало из 1-й точки (вершины конуса) и проходящих через плоскую поверхность.
Основанием является круг. Если установить модель конуса основанием на горизонтальную поверхность и посмотреть на нее сбоку, она предстанет перед глазами как треугольник.
Однако в зависимости от угла, под которым смотрят на фигуру, нижняя ее часть, может превращаться в полукруг, поэтому при изображении конуса следует учитывать угол зрения. Также важно, с которой стороны на фигуру падает свет для последующего наложения штриховки.

Рисовать карандашом объемную геометрическую фигуру конуса следует следующим образом:
Цилиндр
Цилиндр имеет 2 основания – внизу и вверху. Оба они имеют форму круга и абсолютно равны по размеру. Образующая цилиндра – вертикаль, расположенная перпендикулярно основанию.

Рисунок геометрических фигур карандашом в форме цилиндра выполняется в следующем порядке:
Шар считается простейшей фигурой, недаром такую форму под воздействием сил природы приобретают все планеты и звезды. Однако изобразить шар – задача не из простых.
Первые трудности могут возникнуть с рисованием окружности, затем приходится сталкиваться с серьезными проблемами, появляющимися при штриховке.
Перед работой модель шара рекомендуется осветить мягким светом. В этом случае не будет резких теней, что значительно упростит задачу.
Последовательность рисования шара следующая:




Для рисования натюрмортов из геометрических фигур необходимо:
Для начинающего художника рисование геометрических фигур карандашом подобно обучению алфавита для тех, кто изучает язык. Такая тренировка поможет в дальнейшем при создании сложных фигур и композиций на бумаге.
Видео о рисовании геометрических фигур
Рисунок геометрических фигур карандашом:
Ghenadie Sontu Fine Art
BLOG
Рисование геометрических тел
Главная задача учебного рисунка — изучение и практическое рисование с натуры многообразных форм, созданных природой и человеком. Рисуя с натуры какой-либо конкретный предмет, нужно постоянно возвращаться к повторению общих понятий и принципов учебного рисунка, чтобы они твердо вошли в сознание и в конце концов применялись бы при рисовании автоматически, без лишней затраты времени, без лишних физических и умственных усилий.
Практическая часть пособия построена по принципу последовательного возрастания трудности заданий: от рисования простых геометрических тел до работы над такими сложными по внутреннему строению и внешней пластике формами, как человек и архитектура. Освоение принципов рисунка, его технического и графического исполнения осуществляется сначала на простых формах геометрических тел и предметов быта, для рисования которых достаточно представления о внешнем облике, а затем на голове и фигуре человека, в изображении которых решающую роль играет знание внутренней конструкции и умение увидеть связь анатомического строения с внешней формой.
Эти упражнения являются достаточно хорошей школой для приобретения необходимых основ мышления и навыков в рисунке, владея которыми можно решать любые задачи, в том числе и рисования архитектурных сооружений. Опираясь на общие принципы, практическая часть пособия показывает применение единого метода в изучении и рисовании различных форм.
Методические таблицы на примерах конкретных форм и определенных задач иллюстрируют стадии практического ведения рисунка — от композиционного размещения и линейного построения до тонального решения.
Последовательность выполнения учебного рисунка на листе бумаги такова:
пометка композиционного размещения крайними точками;
нахождение геометрического центра композиции, от которого должно идти дальнейшее построение;
пометка точками основных конструктивных узлов с учетом пропорций и перспективы и нанесение линиями направлений движения основных масс;
прорисовка линиями больших форм с последующей дорисовкой деталей;
нанесение светотени, начиная с линий собственных теней, проработки теней и кончая моделировкой формы на свету;
обобщение и придание цельности рисунку.
На каждой стадии работы необходима строгая проверка и исправление ошибок, допущенных в предыдущих стадиях.
В методических таблицах проведен принцип применения минимума средств для решения той или иной задачи и разумного использования точек, линий и тушевки, различной их силы в начале, середине и конце выполнения работы.
Прежде чем приступить к выполнению рисунка, поставить первую точку и провести первую линию, нужно осознать, что и для чего делать и в какой последовательности во времени вести работу. Необходимо учитывать, что человек не может сразу ответить на все вопросы правильно, ему свойственно ошибаться, поэтому манера в начале работы должна быть такой, которая обеспечивает возможность ясно видеть ошибки и исправлять их с минимальной затратой времени и усилий. Последнее достигается использованием в рисунке точек и линий различной силы.
Первые пометки на листе бумаги в учебном рисунке как с натуры, так и по представлению должны быть слабыми, скупыми или, как говорят, исчезающими, а после анализа и сравнения с натурой исправления следует вносить более сильной линией. Первые пометки по контрасту с последующими при этом становятся незаметными, а к резинке при такой манере учебного рисунка приходится прибегать крайне редко — тогда, когда ошибочная пометка сделана настолько сильно, что спорит с правильной и мешает видеть рисунок. Стирать ошибочные пометки рекомендуется только после того, как найдены правильные.
Большое значение имеют кратковременные рисунки с натуры и по представлению. Поэтому перед тем, как делать длительный учебный рисунок с той или другой точки зрения, рекомендуется осмотреть рисуемый предмет-модель со всех сторон и сделать с характерных точек кратковременные рисунки-наброски, как правило, линейные, позволяющие полнее изучить рисуемую форму в целом, более уверенно и успешно вести длительный рисунок с нее. С помощью набросков можно получить ясное представление о внешней форме, о движении в пространстве и о пропорциях рисуемого объекта. Если форма предмета сложная, то для ясного ее понимания полезно сделать мысленно ряд сечений плоскостью и изобразить эти сечения на бумаге линией. Иногда быстрый набросок может решать одну из частных задач рисунка: в одном случае — конструктивную, в другом — задачу пропорций и передачи характера, в третьем — движения, светотени или композиции. Для решения каждой из задач следует выбирать соответствующую манеру изображения и степень законченности.
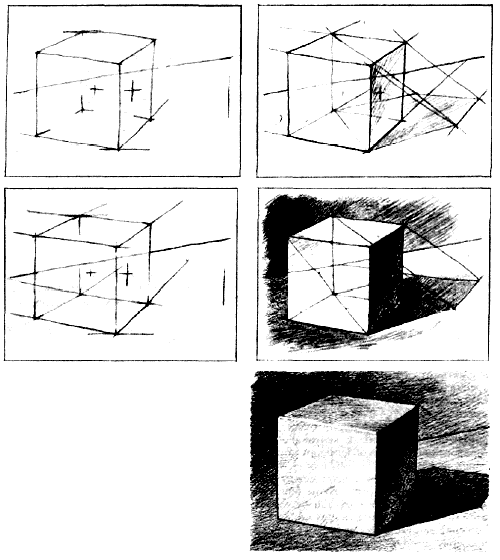
Рис 1. Последовательность рисунка куба
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это это часть плоскости, которая лежит внутри окружности.
Окружность — это граница круга.
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.