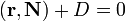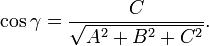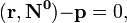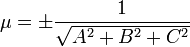Что такое геометрическая плоскость
Плоскость

Всего получено оценок: 106.
Всего получено оценок: 106.
Плоскость – это основная единица планиметрии. Для правильного восприятия сложных фигур, таких как, пирамида, конус или призма, необходимо понимать и, главное, представлять себе, что такое плоскость.
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Способы задания плоскостей
Плоскость может быть задана тремя точками, нележащими на одной прямой. Из этого утверждения следуют еще два варианта задания плоскостей. При этом специального знака плоскостей не существует.
Плоскость можно задать двумя пересекающимися прямыми, тогда одной точкой будет служить точка пересечения прямых, а двумя другими произвольные точки на одной и второй прямой.
Еще один вид это задание прямой и точкой, нележащей на этой прямой. По аналогии со вторым вариантам: одна точка уже есть и не лежит на прямой, а две других это произвольные точки имеющейся линии.
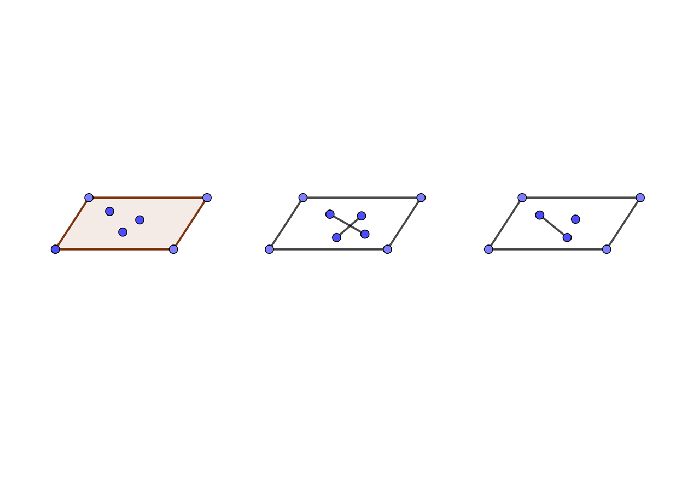
Взаимное расположение прямой и плоскости
Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.
Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.
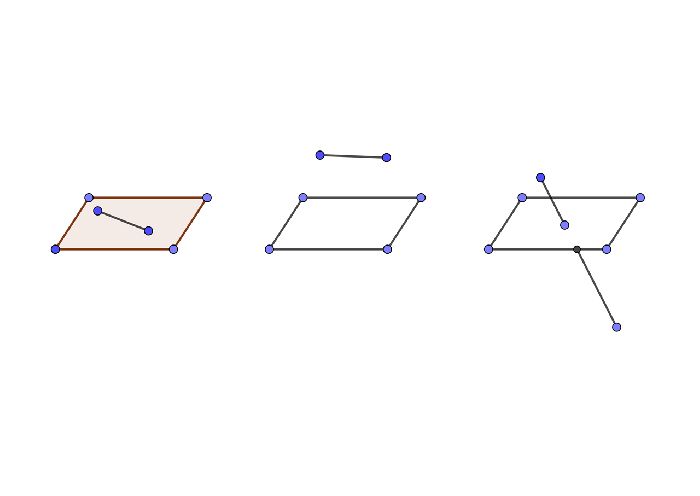
Взаимное расположение плоскостей
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.
Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.
Что мы узнали?
Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.
Плоскость (в математике)
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Содержание
Некоторые характеристические свойства плоскости
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
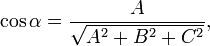
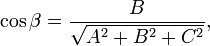
(смешанное произведение векторов), иначе
где 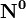
(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между параллельными плоскостями
Связанные понятия
Если в векторной форме, то
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Полезное
Смотреть что такое «Плоскость (в математике)» в других словарях:
ПЛОСКОСТЬ — ПЛОСКОСТЬ, в математике плоская поверхность, такая, что любая прямая, соединяющая две ее точки, целиком принадлежит этой поверхности. Общее уравнение плоскости в трехмерной декартовой системе координат выглядит как ах+by+cz=d, где а, b, с и d… … Научно-технический энциклопедический словарь
Плоскость Минковского — В математике, плоскость Минковскогоe двумерное аффинное пространство снабжённое метрикой которая инвариантна относительно параллельных переносов. Названа в честь Минковского. Часто данное аффинное пространство ототожествляют с плоскостью R2.… … Википедия
Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
соприкасающаяся плоскость — в точке M кривой l, плоскость, имеющая с l в точке М касание порядка п≥2. См. Соприкосновение,Кручение. * * * СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ в точке M кривой l, плоскость, имеющая с l в точке M касание порядка nі2. См.… … Энциклопедический словарь
Симметрия (в математике) — Симметрия (от греч. symmetria ‒ соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), ‒ преобразование пространства (плоскости), при… … Большая советская энциклопедия
Расстояние в математике — Метрическим пространством называется множество, в котором определено расстояние между любой парой элементов. Содержание 1 Формальное определение 2 Обозначения 3 Примеры … Википедия
Координаты в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Координаты, в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Плоскость в пространстве – необходимые сведения, способы задания плоскости, плоскости в пространстве
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Взаимное расположение прямой и плоскости
Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.
Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.
Рис. 2. Взаимное расположение прямой и плоскости.
Параллельные плоскости
Теперь рассмотрим подробнее каждый из названных выше случаев. Предположим, что в общей форме заданы следующие две плоскости:
A1*x + B1*y + C1*z + D1 = 0;A2*x + B2*y + C2*z + D2 = 0.
Как понять, являются ли они параллельными? Сделать это очень просто. Достаточно вспомнить о нормальных векторах. Если две плоскости параллельны между собой, значит, их нормали также параллельны. Выпишем координаты нормальных векторов к указанным плоскостям. Имеем:
Достаточным условием параллельности n1¯ и n2¯ является возможность задания одного из них через другой. Математически это записывается так:
Где k — некоторое (в том числе отрицательное) число. Если одну нормаль невозможно выразить путем умножения координат другой на число, то такие плоскости не будут параллельными.
Частным случаем параллельности плоскостей является их полное совпадение друг с другом. Тогда должны выполняться такие условия:
Пример параллельных плоскостей в пространстве приведен ниже.
Пересекающиеся плоскости и угол между ними
Поскольку существует всего два варианта взаимного расположения плоскостей, то достаточно проверить, являются ли они параллельными или нет. В случае их пересечения часто возникает необходимость в определении соответствующего угла. Согласно определению, углом между рассматриваемыми геометрическими объектами является угол между их нормалями.
Таким образом, изучая вопрос взаимного расположения плоскостей и угла между плоскостями, достаточно рассчитать скалярное произведение векторов n1¯ и n2¯. Соответствующая формула примет вид:
Угол между плоскостями θ всегда является острым, поскольку в числителе стоит модуль скалярного произведения.
Следует отметить частный случай, когда две плоскости пересекаются под углом 90o. Тогда достаточно вычислить скалярное произведение нормальных векторов. Оно будет равным нулю.
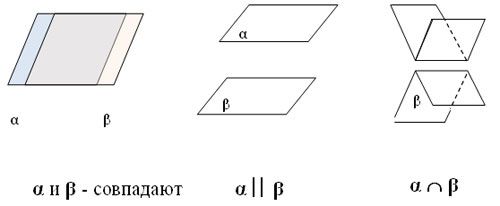
Взаимное расположение плоскостей
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.
Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.
Рис. 3. Расположение плоскостей.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат Охуz в трехмерном пространстве. Координатные векторы i→, j→, k→ считаются нормальными векторами плоскостей Oyz, Oxz и Oxy. Это суждение верно, так как i→, j→, k→ ненулевые и расположены на координатных прямых Ox, Oy и Oz. Эти прямые перпендикулярны координатным плоскостям Oyz, Oxz и Oxy.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат Охуz. Для определения нормального вектора n→=(A, B, C) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид Ax+By+Cz+D=0. То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2x-3y+7z-11=0.
Определить координаты направляющих векторов заданной плоскости x+2z-7=0.
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x+2z-7=0 к виду 1·x+0·y+2z-7=0. Отсюда получим, что координаты нормального вектора данной плоскости равны (1, 0, 2). Тогда множество векторов будет иметь такую форму записи (t, 0, 2·t), t∈R, t≠0.
Ответ: (t, 0, 2·t), t∈R, t≠0.
При помощи уравнения плоскости в отрезках, имеющего вид xa+yb+zc=1, и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1a, 1b, 1c.
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Основные понятия геометрии. Понятие точки, прямой и плоскости
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия.
Прямая и плоскость безграничны, поэтому на чертеже изображают часть.
Точка – это самая простая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура – это множество точек, обладающих определенным свойством, характерным только для этой фигуры.
Прямую можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком (или отрезком прямой). Основное свойство отрезка – это его длина. Длина отрезка – это расстояние между его концами. Измерить отрезок – это значит установить его длину в определенных единицах. Основные единицы измерения длины: миллиметр (мм), сантиметр (см), дециметр (дм), метр (м), километр (км).
Отрезок изображается так:
Луч – это направленная полу прямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку, то этой точкой прямая разбивается на два противоположно направленных луча. Такие лучи называются дополнительными.
Плоскость, как и прямая, – это первичное понятие, не имеющее определения. У плоскости, как и у прямой, невозможно увидеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную геометрическую фигуру:
Взаимное расположение прямой и точки
Возможны два варианта взаимного расположения прямой и точки на плоскости:
– либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку);
– либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Аксиома – это утверждение, устанавливающее некоторое свойство и принимаемое без доказательства.
Основные свойства принадлежности точек и прямых
Основные свойства взаимного расположения точек на прямой и на плоскости
Основные свойства измерения отрезков
Основные свойства откладывания отрезков
Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путем рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы.
ПЛОСКОСТЬ
Смотреть что такое «ПЛОСКОСТЬ» в других словарях:
ПЛОСКОСТЬ — ПЛОСКОСТЬ, плоскости, мн. плоскости, плоскостей, жен. 1. только ед. отвлеч. сущ. к плоский (книжн.). Плоскость груди. Плоскость острот. 2. Поверхность, имеющая только два измерения, так что между любыми двумя точками ее можно провести прямую,… … Толковый словарь Ушакова
плоскость — См … Словарь синонимов
плоскость X-Y — горизонтальная плоскость Плоскость, определяемая осями X и Y [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы горизонтальная плоскость EN X Y plane … Справочник технического переводчика
ПЛОСКОСТЬ — простейшая поверхность. Понятие плоскость (подобно точке и прямой) принадлежит к числу основных понятий геометрии. Плоскость обладает тем свойством, что любая прямая, соединяющая две ее точки, целиком принадлежит ей … Большой Энциклопедический словарь
Плоскость — период времени, в котором цена не повышается и не падет. Плоскость период времени, когда закрыты все позиции. По английски: Flat См. также: Тренды Финансовый словарь Финам … Финансовый словарь
плоскость U — U плоскость обрабатывает данные пользователя, проходящие через систему G PON. U плоскость обеспечивает связь между клиентами ATM или клиентами GEM (МСЭ Т G.984.3). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики… … Справочник технического переводчика
ПЛОСКОСТЬ — ПЛОСКОСТЬ, простейшая поверхность такая, что любая прямая, проходящая через 2 ее точки, принадлежит ей … Современная энциклопедия
ПЛОСКОСТЬ — ПЛОСКОСТЬ, и, мн. и, ей и ей, жен. 1. см. плоский. 2. (ей). В геометрии: поверхность, имеющая два измерения. Линия на плоскости. 3. (ей). Ровная, гладкая поверхность. По наклонной плоскости катиться (также перен.: опускаться в нравственном… … Толковый словарь Ожегова
плоскость — плоскость, мн. плоскости (неправильно плоскостя), род. плоскостей и плоскостей … Словарь трудностей произношения и ударения в современном русском языке