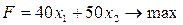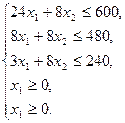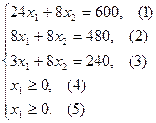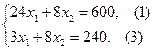Что такое геометрическая интерпретация

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №39. Геометрическая интерпретация комплексного числа.

Перечень вопросов, рассматриваемых в теме

3) определение модуля комплексного числа.

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Геометрическое изображение комплексных чисел.

а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).

Модуль комплексного числа

Как отмечалось выше, комплексное число также можно изображать радиус-вектором (рис. 4).

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Иногда еще модуль комплексного числа обозначается как r или ρ.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Найдите модуль комплексного числа z=5-3i

Решим данное задание, используя определение модуля.

Верный ответ: 2.

№2. Тип задания: рисование.

Изобразите вектором на комплексной плоскости точку z=2+3i

Разобьем z=2+3i на две части: z₁=2 и z₂= 3i. Отметим на плоскости точки О и А, соединим их:

Источник

Комплексные числа

Известно, что квадратное уравнение с вещественными коэффициентами и отрицательным дискриминантом не имеет вещественных корней. В частности, уравнение
$$
z^2+1=0\nonumber
$$
не имеет корней на множестве \(\mathbb\). Возникает потребность расширить множество \(\mathbb\) так, чтобы на более широком множестве было разрешимо квадратное уравнение с любыми вещественными коэффициентами.

Определение комплексного числа.

Комплексными числами называют пары \((x,y)\) вещественных (действительных) чисел \(x\) и \(y\), для которых следующим образом определены понятие равенства и операции сложения и умножения.
Обозначим комплексное число \((x,y)\) буквой \(z\), то есть положим \(z=(x,y)\). Пусть \(z_1=(x_1,y_1)\), \(z_2=(x_2,y_2)\). Два комплексных числа \(z_1\) и \(z_2\) считаются равными тогда и только тогда, когда \(x_1=x_2\) и \(y_1=y_2\), то есть
$$
\<(x_1,y_1) = (x_2,y_2)\>\Leftrightarrow \\ \wedge\ \.\nonumber
$$

Сумма и произведение комплексных чисел \(z_1\) и \(z_2\) обозначаются соответственно \(z_1+z_2\) и \(z_1z_2\) и определяются формулами
$$
z_1+z_2=(x_1+x_2,y_1+y_2),\label
$$
$$
z_1z_2=(x_1x_2-y_1y_2,x_1y_2+x_2y_1).\label
$$

Из формул \eqref и \eqref следуют соотношения
$$
(x_1,0) + (x_2,0) = (x_1+x_2,0),\qquad (x_1,0)(x_2,0) = (x_1x_2,0),\nonumber
$$
которые показывают, что операции над комплексными числами вида \((x, 0)\) совпадают с операциями над действительными числами. Поэтому комплексное число вида \((x, 0)\) отождествляют с действительным числом \(x\), то есть полагают \((x,0) = x\).

Следовательно, любое комплексное число \(z= (x,y)\) можно записать в виде \(x + iy\), то есть
$$
z = x + iy.\label
$$

Запись комплексного числа \(z = (x,y)\) в виде \eqref называют алгебраической формой комплексного числа.

В записи \eqref число \(x\) называют действительной частью комплексного числа и обозначают \(Re\ z\), а число \(y\) — мнимой частью и обозначают \(Im\ z\), то есть
$$
Re\ z = x,\quad Im\ z = y. \nonumber
$$

Если \(x= 0\), то есть \(z = iy\), то такое комплексное число называют чисто мнимым.

Здесь и всюду в дальнейшем, если не оговорено противное, в записи \(x+iy\) числа \(x\) и \(y\) считаются действительными (вещественными).

Число \(\displaystyle\sqrt\) обозначают \(|z|\) и называют модулем комплексного числа \(z\), то есть
$$
|z|=|x + iy|=\sqrt.\label
$$
Заметим, что \(|z|\geq 0\) и \(\<|z| = 0\>\Leftrightarrow \\).

Комплексное число \(x-iy\) называют сопряженным комплексному числу \(z = x + iy\) и обозначают \(\overline\) то есть
$$
\overline = \overline= x-iy.\label
$$
Из равенств \eqref и \eqref следует, что
$$
|z| = |\overline|,\qquad z\overline=|z|^2,\label
$$
так как \(z\overline=(x+iy)(x-iy) = x^2 + y^2\).

Свойства операций.

Операции сложения и умножения комплексных чисел обладают свойствами:

Эти свойства вытекают из определения операций сложения и умножения комплексных чисел и свойств операций для вещественных чисел.

Из уравнения \eqref в силу правила равенства и определения суммы комплексных чисел следует, что
$$
z_1-z_2=(x_1-x_2)+i(y_1-y_2).\nonumber
$$

Деление на множестве \(\mathbb\) вводится как операция, обратная умножению, а частным от деления комплексного числа \(z_1=_1+iy_1\) на число \(z_2 = x_2 + iy_2\) называют такое число \(z\), которое удовлетворяет уравнению
$$
zz_2=z_1\label
$$
и обозначается \(z_1:z_2\) или \(\displaystyle \frac\).

Докажем, что уравнение \eqref для любых комплексных чисел \(z_1\) и \(z_2\), где \(z_2\neq 0\), имеет единственный корень.

\(\circ\) Умножая обе части уравнения \eqref на \(\overline_2\), получим в силу равенства \eqref уравнение
$$
z|z_2|^2 = z_1\overline_2,\label
$$
которое равносильно уравнению \eqref, так как \(\overline_2\neq 0\).

Эту формулу можно не запоминать — важно знать, что она получается умножением числителя и знаменателя на число, сопряженное со знаменателем.

Найти частное \(\displaystyle \frac\), если \(z_1=5-2i,\ z_2=3 + 4i\).

Источник

Геометрическая интерпретация и графическое решение задачи линейного программирования

Геометрическая интерпретация задач дает возможность наглядно представить их структуру, выявить особенности. Задачу линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно.

Рассмотрим случай двух переменных:

(5)

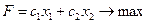
Дадим геометрическую интерпретацию элементов этой задачи.

Каждое из ограничений (6), (7) задаёт на плоскости x₁Ox₂ некоторую полуплоскость. Полуплоскость – выпуклое множество. Напомним, что выпуклым называют множество, которое вместе с любыми своими точками x₁ и x₂ содержит и все точки отрезка [ x₁; x₂]. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений (ОДР) задачи есть выпуклое множество.

Возможны ситуации, когда область допустимых решений ЗЛП:

— неограниченная выпуклая многоугольная область;

Геометрическая интерпретация целевой функции.

Пусть ОДР задачи ЛП – непустое множество.

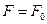
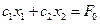
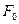
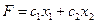
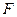
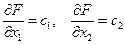
Выберем произвольное значение целевой функции , получим . Это уравнение прямой линии. В точках прямой целевая функция сохраняет одно и то же постоянное значение . Считая в равенстве параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции. Найдем частные производные целевой функции по x₁ и x₂: .

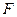
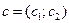
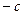
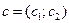
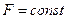
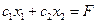
Частная производная функции показывает скорость её возрастания вдоль данной оси. с₁ и с₂ – скорости возрастания соответственно вдоль осей Ox₁ и Ox₂. Вектор называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор указывает направление наискорейшего убывания целевой функции Его называют антиградиентом.

Вектор перпендикулярен к прямой семейства .

Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения.

1. С учетом системы ограничений строится область допустимых решений.

2. Строится вектор .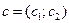

3. Проводится произвольная линия, перпендикулярная к вектору .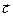

4. При решении задачи на максимум перемещается линия уровня в направлении вектора 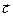так, чтобы она касалась области допустимых решений в ее крайнем положении.

В случае задачи на минимум линия уровня перемещается в антиградиентном направлении.

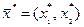
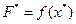
5. Определяется оптимальный план и экстремальное значение целевой функции .

Возможны следующие случаи:

— оптимальный план единственный;

— оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через сторону области допустимых решений;

— целевая функция неограниченна;

— область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального и минимального значения;

— задача не имеет решения: ОДР – пустое множество, т.е. система ограничений задачи несовместна.

Пример. Пусть предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами 3-х видов С, D и E в объёмах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и даны в таблице 1. Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В- 50 млн. руб. Требуется найти объёмы производства изделий, обеспечивающие максимальную прибыль.

Решение. Построим математическую модель задачи.

— количество деталей A,

— количество деталей B,

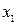
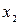
Ограничения будут иметь вид:

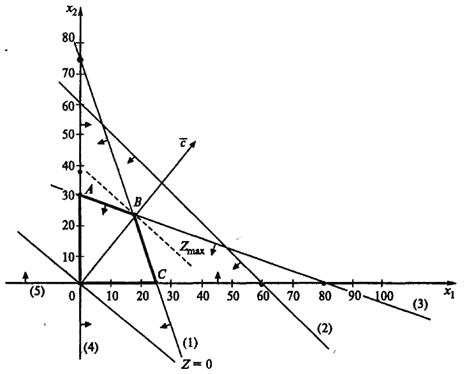
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений-неравенств запишем в виде уравнений и пронумеруем их:

Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

Чтобы построить первую прямую, найдем точки её пересечения с осями координат: при x₁ = 0, х₂ = 75, а при х₂ = 0, x₁ = 25. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку 0(0,0) и подставим ее координаты в неравенство — оно удовлетворяется. Так как точка 0(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой 24х₁ + 8х₂ = 600. На рис. 1 расположение полуплоскости относительно первой прямой отмечено стрелками.

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенствам. Точки, удовлетворяющие ограничениям х₁, ³ 0, х₂ ³ 0, находятся в первом квадранте.

Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. На графике (рис. 1) это многоугольник ОАВС.

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что данная задача линейной оптимизации имеет множество допустимых решений, т.е. многовариантна. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.

Приравняем функцию к нулю и построим соответствующую прямую. Вектор-градиент прямой функции 40х₁ + 50х₂ = 0 имеет координаты 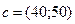. Изобразим вектор на графике и построим прямую перпендикулярно этому вектору (рис. 1). Перемещая прямую функции параллельно самой себе в направлении вектора, увидим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения.

Координаты точки В найдем, решая систему уравнений, прямые которых пересекаются в данной точке:

Решив эту систему, получим, что х₁ = 17,14; х₂ = 23, 57. Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную

Z_max = 40×17,14 + 50×23,57 = 1 864,1(млн. руб.).

Источник

Геометрическая интерпретация

Геометрическая интерпретация

записан в виде разложения / =Со?о+^1? 1 + • • • = / o+ / 1 + • • • + / т+ • • • — Каждый вектор Людмила Фирмаль

/ представлен в виде C u m M s для всех компонентов в направлении главных «ортов». Это геометрический смысл расширения рядов Фурье! U R a V n e n I E s a M K n U t O s t I[n°413], в терминах(12), записывается следующим образом: Или Квадрат длины «вектора» равен сумме

квадратов длин всех его составляющих. Это естественное обобщение Тео Р ЭМ С П и Ф А го Р а (соответствующее случаю Д У М е р н о г о вектора, разложенного на компоненты, перпендикулярные друг другу). Вспомнихм и о б о б щ е н О Е Р А В Н И Е З А М К Н у Т О С Т

, перпендикулярные друг другу[n°388,(1)]. Для углубления сходства между»пространством» рассматриваемой функции и обычным евклидовым пространством сначала расширяют класс рассматриваемой функции, а затем используют оба набора интегралов, которые затем выполняются в ходе так называемой теории функций вещественных

переменных[см. раздел VI, К Л Ю Ч Е Н Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Геометрическая и алгебраическая интерпретация математических понятий

Описание разработки

Софии Жермен: «Алгебра – не что иное, как записанная в символах геометрия, геометрия – это просто алгебра, воплощенная в фигурах».

Существуют способы решения алгебраических задач методами,

История математики свидетельствует о том, что оба метода, алгебраический и геометрический развивались в тесной взаимосвязи. В классическую греческую эпоху геометрия занимала привилегированное положение. Она являлась именно той наукой, в которой проявлялся дедуктивный характер рассуждения, искусство доказательства. Первые элементы алгебры появились сразу в интерпретациях: геометрический и буквенно-символической. Систематизация алгебраических сведений построение алгебры как особой части математики проходило также в двух равносильных и равноправных интерпретациях. Этот набор методов было принято называть геометрической алгеброй. Благодаря взаимосвязи алгебраического и геометрического методов были сделаны многие открытия в математике.

Геометрический метод состоит в том, что само доказательство или решение задачи направляется наглядным представлением. Основное
преимущество геометрического метода в его наглядности. Он позволяет увидеть то, что в алгебраическом методе скрыто за аналитическими выкладками. Кроме того, выполненный рисунок позволяет рассуждать, делать выводы. Недаром еще великий Р. Декарт в своем труде «Правила для руководства ума» специально выделял правило о том, что «полезно чертить фигуры и преподносить их внешним чувствам, для того,
чтобы таким образом нам было легче сосредоточивать внимание нашего ума».

Цели данной работы:

1. Показать, что преимущество геометрического решения алгебраических задач в его наглядности, так как геометрический подход допускает изящное решение.

2. Выявить связи между, казалось бы, совершенно разнородными темами школьного курса математики.

Рассмотреть ряд приёмов решения нестандартных и конкурсных

Практическая помощь учителям математики.

Между алгебраическими и геометрическими задачами, между языком алгебры (языком формул) и языком геометрии (языком расстояний) существует неразрывная связь, ставшая со времен Декарта очевидной даже тем, кто не слишком искушен в математике. В самом деле, решение многих геометрических задач может быть сведено к решению систем алгебраических уравнений и требует умения применять соответствующий алгебраический инструмент.

Алгебраический язык (язык формул)

Геометрический язык (язык расстояний)

Расстояния до координатных осей (координаты)

Модуль разности двух чисел

Расстояние между двумя точками координатной прямой

Сумма квадратов двух чисел

Квадрат расстояния между двумя точками координатной плоскости

2. Геометрический метод алгебраических задач

2.1. Решение уравнений и неравенств с модулем.

Аналогично решается уравнение |f(x)|=g(x). Действительно, если g(x) 0, то f(x)=g(x); f(x)=-g(x).

Другой способ решения состоит в рассмотрении двух случаев при освобождении от знака модуля: |f(x|=f(x) при f(x) > 0, |f(x|—f(x) при f(x)

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ КЕМЕРОВСКОЙ ОБЛАСТИ

Государственное образовательное учреждение среднего профессионального образования

Кемеровский профессионально-технический техникум

Геометрическая и алгебраическая интерпретация математических понятий

Выполнил преподаватель математики:

Коровина Нина Анатольевна.

Математические утверждения 4

2. Геометрический метод алгебраических задач 4

2.1. Решение уравнений и неравенств с модулем 4

2.2. Решение систем неравенств 7

2.3. Решение квадратных уравнений 8

2.4. Решение иррациональных уравнений и неравенств 9

2.5. Решение текстовых задач 11

2.6. Решение задач на наибольшее и наименьшее значения функции 12

2.7. Решение задач на нахождение площади фигуры, заданной на координатной плоскости 14

Источник