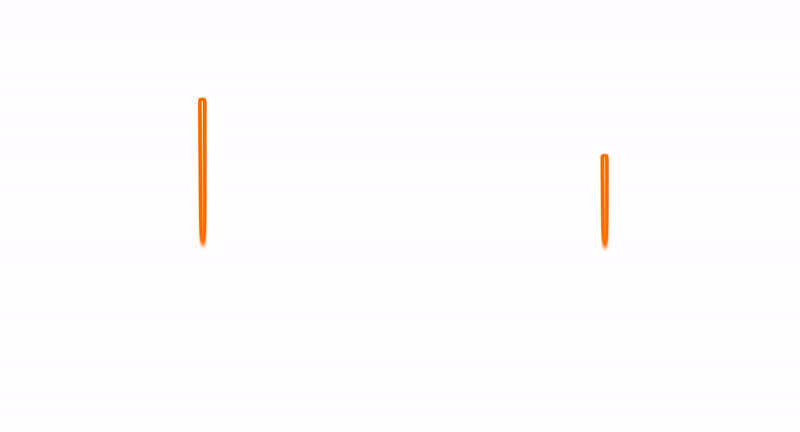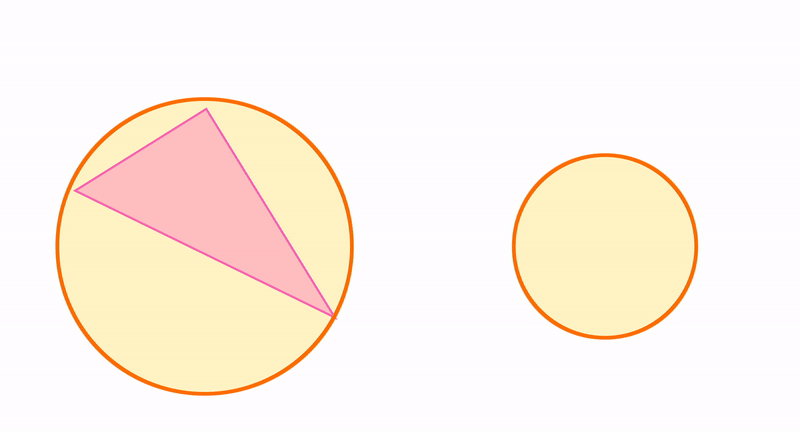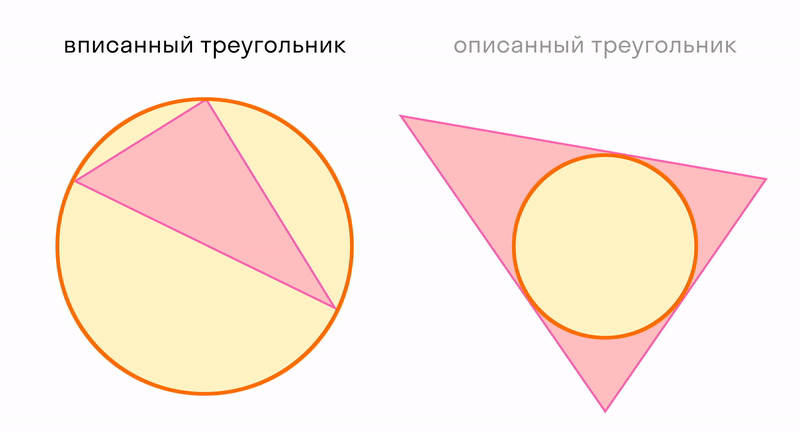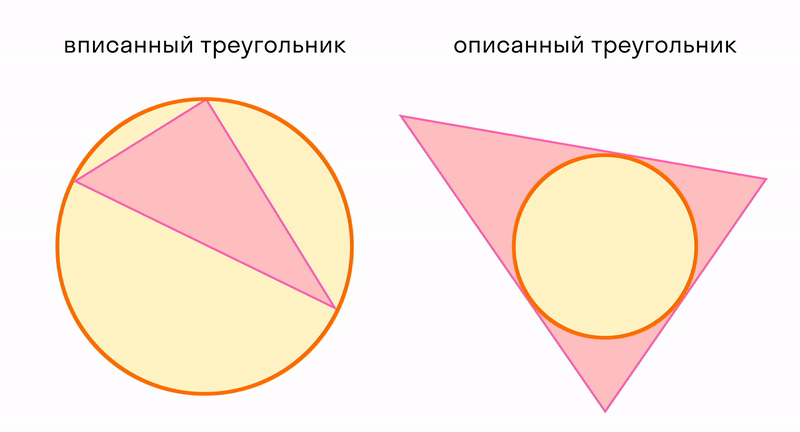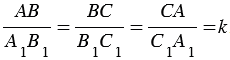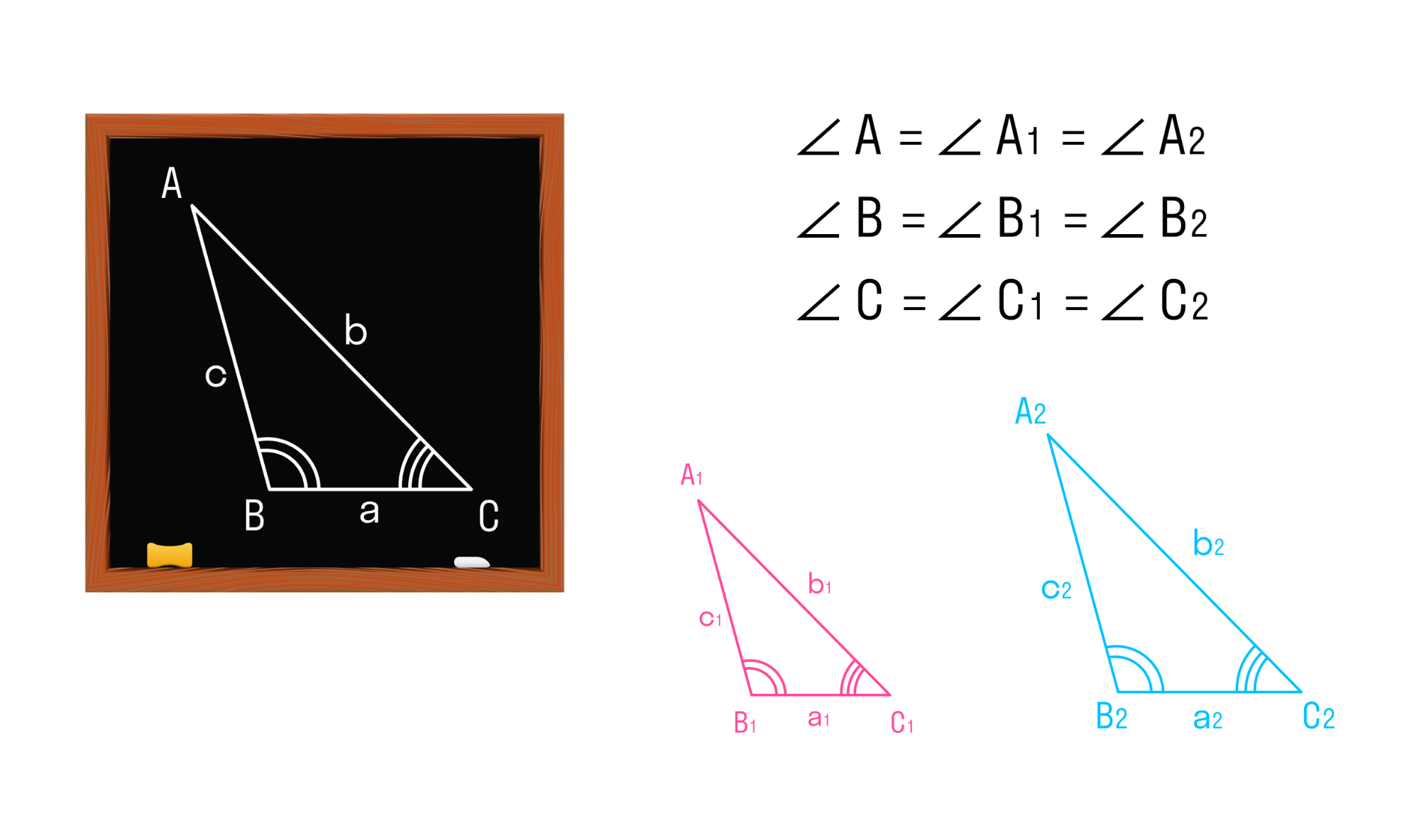Что такое геометрическая фигура в математике
Общая характеристика
Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.
Основные понятия о составляющих
Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.
Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).
Виды линий:
Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.
Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.
Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.
Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объекты
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.
Виды треугольника в зависимости от угла (У):
Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.
Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.
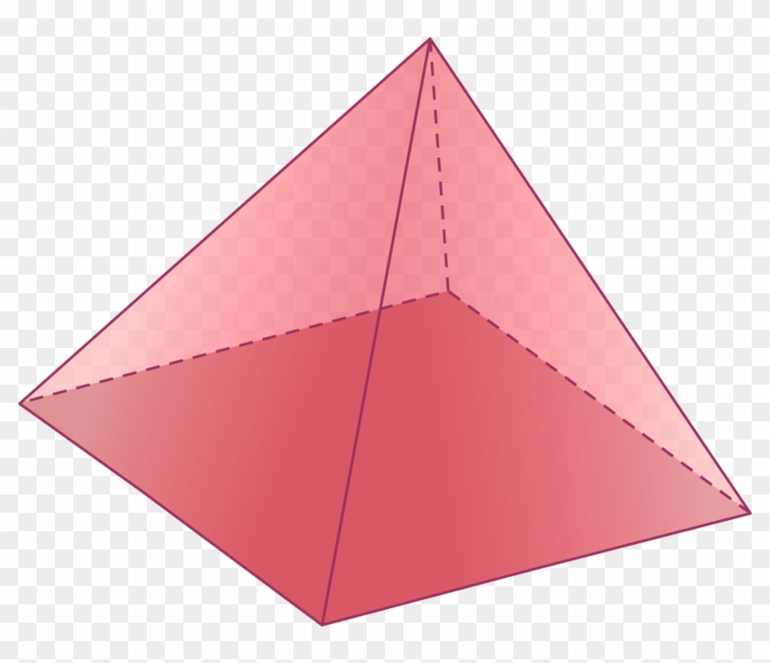
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.
Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.
Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
Сложные модели
В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.
Определение тела и пространства
Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.
Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).
Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.
В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).
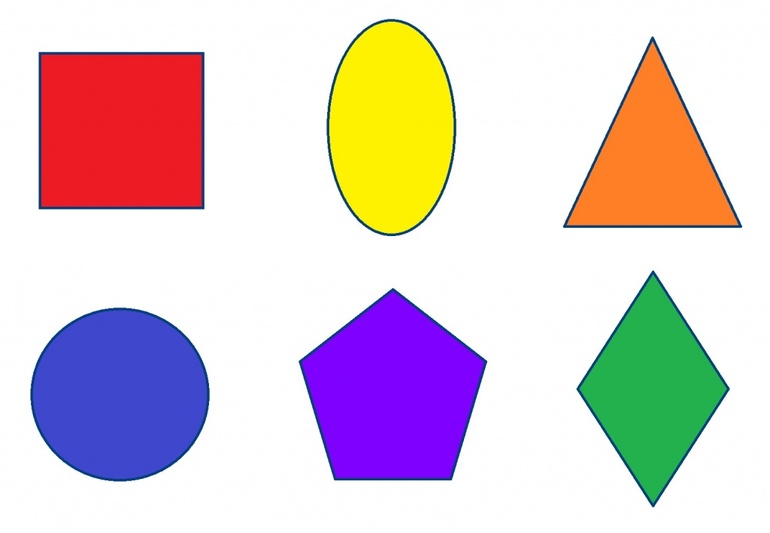
Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.
Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.
Объемные фигуры:
Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.
Виды многогранников:
В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.
Познавательные игрушки детям
Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.
Основной материал для обучения детей:
Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.
Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.
Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.
Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.
Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.
Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.
Геометрические фигуры и их названия
При изучении элементарной геометрии необходимо точно определить, что именно мы будем изучать. Каждая наука ставит в центр внимания определенные объекты, или понятия, которые должны быть четко и однозначно определены. Это нужно, чтобы у оппонентов не возникало причин для оспаривания полученных в ходе эксперимента или теоретических разработок выводов.
Геометрии это касается в полной мере. Это одна из самых древних наук, возникшая из необходимости измерения площадей земельных участков, длины пути, расстояния между городами. Позже предметом прикладной геометрии стали архитектурные проекты, определение положения звезд и вычисление размеров земли. Но сугубо прикладных функций, полезных в повседневной жизни, она не утратила.
Геометрические фигуры
Первый вопрос, на который нужно ответить при изучении раздела, является ли точка геометрической фигурой? Ответ сформулировал еще Эвклид — точка, это простейшая фигура, элемент, из которого состоят все остальные фигуры. Линия, как ошибочно думают многие, не элементарная фигура, а совокупность точек.
Из точек состоят все простые и сложные геометрические построения. Это единственная фигура, размеры которой нельзя определить и указать, как нельзя и ничего определенного сказать о количестве точек в длинной или короткой линии, как нельзя определить с достаточно высокой точностью количество атомов в массивном бесформенном куске железа или камня.
Простейшие фигуры
Из точек можно создать любые линии, прямые, закругленные, зигзагообразные. Вариантов множество. Линия — вторая по простоте фигура после точки. Все линии подразделяются на несколько видов:
Прямая — бесконечная последовательность точек, определяющая кратчайшее расстояние между двумя произвольными точками. Крайние пункты могут быть расположены как на расстоянии в несколько миллиметров, так и на противоположных концах Вселенной. Но важно одно, прямая проходит через эти точки и стремиться дальше, ни начала, ни конца у нее нет.
Отрезок — частичный случай прямой. Это то же расстояние между двумя точками, но линия начинается на одной из них, и заканчивается на другой. Длина отрезка — величина вполне определенная измеряемая при помощи линейки, циркуля или рулетки, в зависимости от того, где находится данный отрезок.
Луч — часть прямой, лежащая по одну сторону от выбранной точки. Луч имеет начало, но не имеет конца. Как пример геометрического луча можно привести луч фонарика или лазерной указки. Началом является лампочка или светодиод, а дальше луч распространяется как угодно далеко.
Ломаная линия — совокупность отрезков, которые имеют по одной общей точке (начало следующего отрезка является концом предыдущего), но не лежат на одной прямой. Ломаная линия может быть как замкнутой, так и незамкнутой. Если линия замкнута, то образует другой геометрический объект — плоскую фигуру.
Дуга — совокупность точек, которые находятся на одной линии, но не на одной прямой. Частичный случай — фрагмент окружности.
Как уже говорилось, замкнутые ломаные линии образуют плоские фигуры. Почему плоские, мы рассматриваем только линии, которые находятся в системе координат XY, то есть, всех их можно нарисовать на листе бумаги не прибегая к такой сложной технике, как перспектива.
Треугольник — самая простая и самая устойчивая плоская фигура. Образована тремя отрезками, соединенными последовательно. Чтобы построить треугольник, необходимо, чтобы сумма длин любых двух отрезков превышала длину третьего. В зависимости от длин отрезков и углов между ними, треугольники подразделяются на равносторонние, равнобедренные, прямоугольные и произвольные (с тупыми и острыми углами).
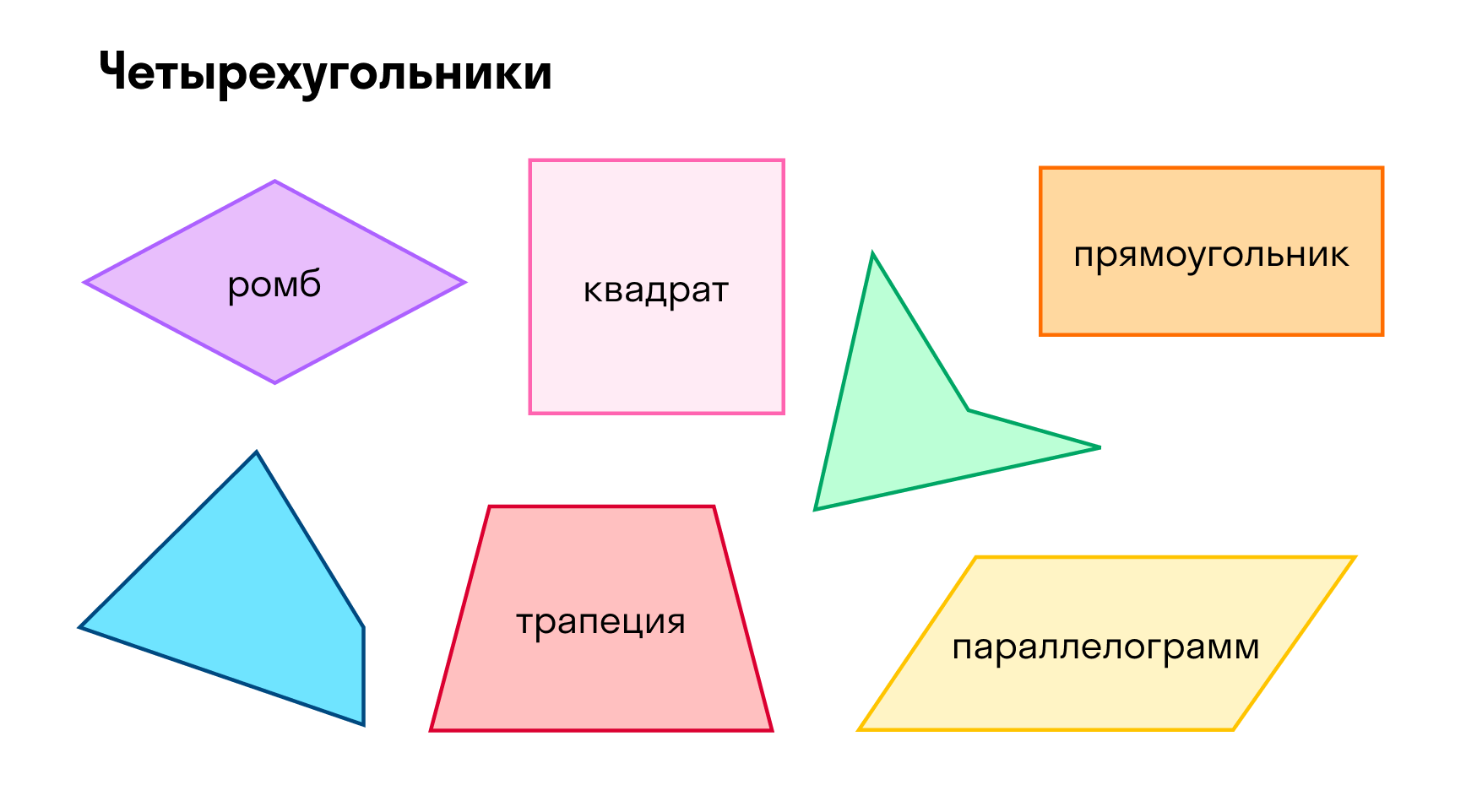
Четырехугольники
Ромб — преобразованный квадрат. Длина всех сторон одинакова, но углы не прямые. Иногда квадрат называют прямоугольным ромбом.
Трапеция — фигура, у которой параллельны только две противоположные стороны, которые называют основанием. В зависимости от расположения двух оставшихся сторон, трапеция бывает прямоугольной и непрямоугольной.
Многоугольники
Назвать все виды фигур в геометрии очень сложно. Но необходимо назвать многоугольники — это категория фигур, у которых количество сторон более 4. Их так и называют — пятиугольник, шестиугольник, восьмиугольник. В научной литературе многоугольники получили название «полигон». Соответственно, пятиугольник — пентагон, восьмиугольник — октагон и т.д.
Круги и овалы
Это фигуры, которые состоят не из отрезков, а из последовательно расположенных точек, находящихся на определенном расстоянии от центра. У кругов это расстояние одинаковое, у овалов — разное.
Объемные фигуры
Если рассматривать геометрические построения в пространстве координат XYZ, то получаются объемные фигуры, или тела. Это куб, конус, цилиндр, шар и другие. Но их изучение — предмет другой темы.
Основы геометрии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
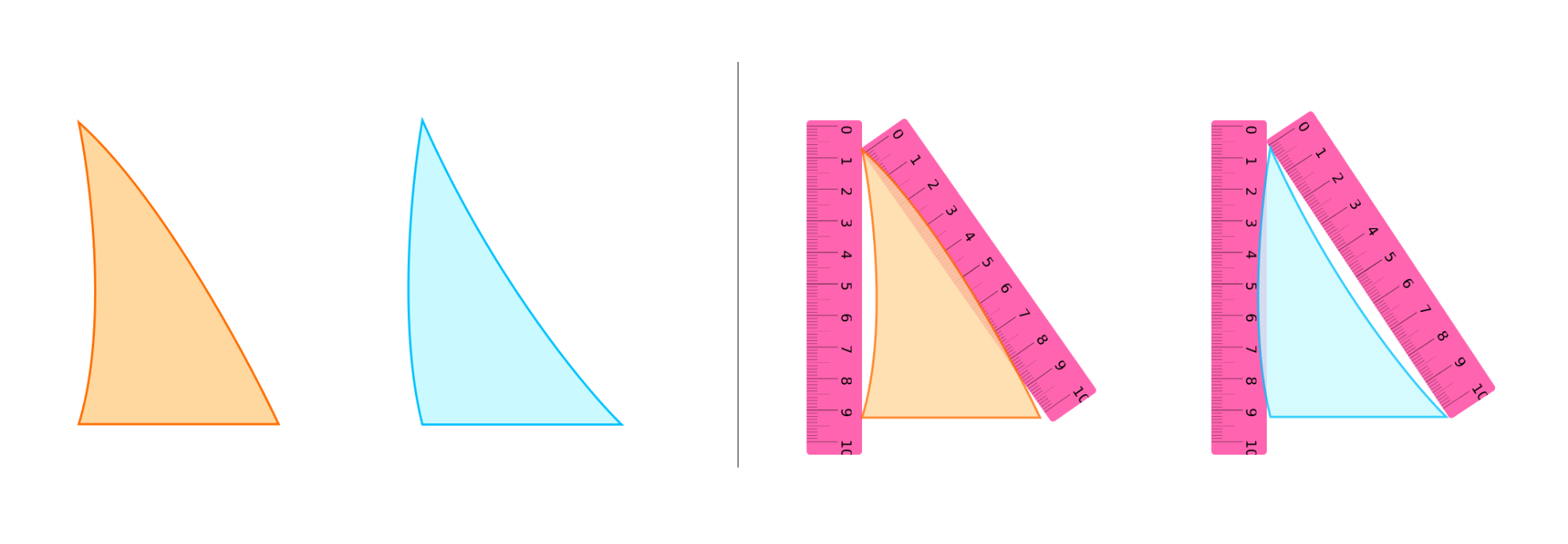
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
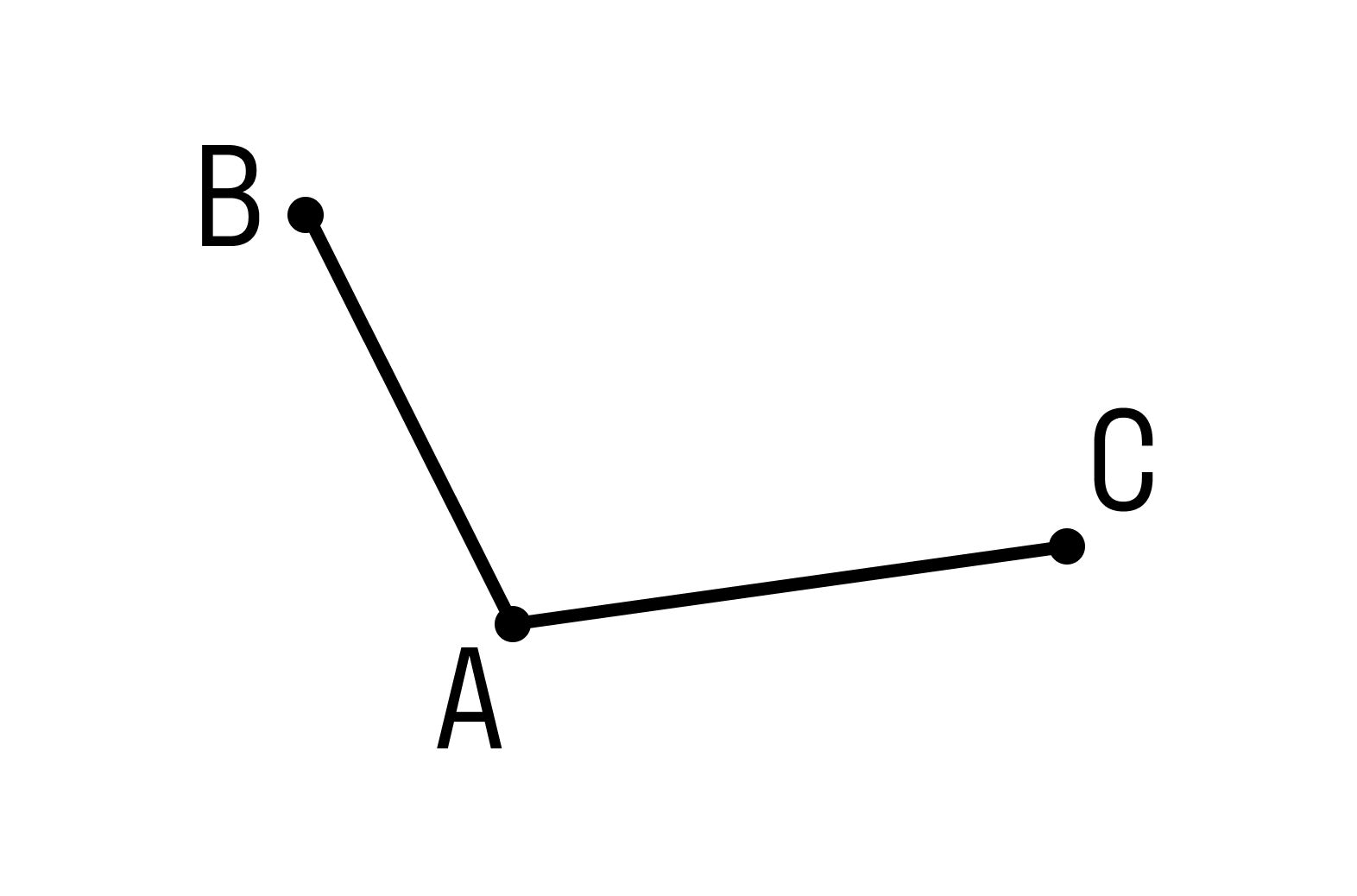
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
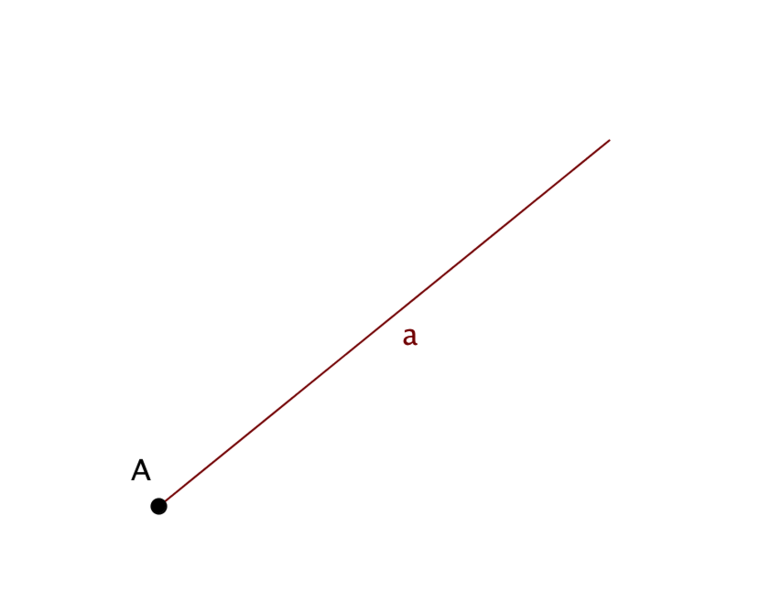
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
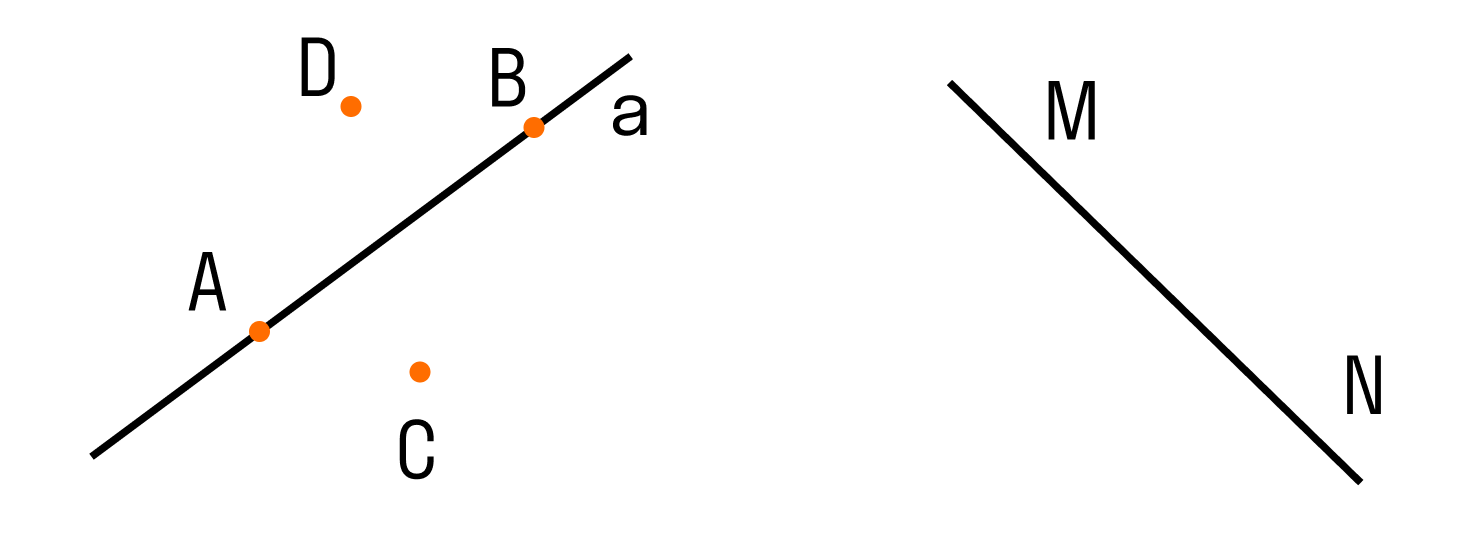
Два варианта расположения точек относительно прямой:
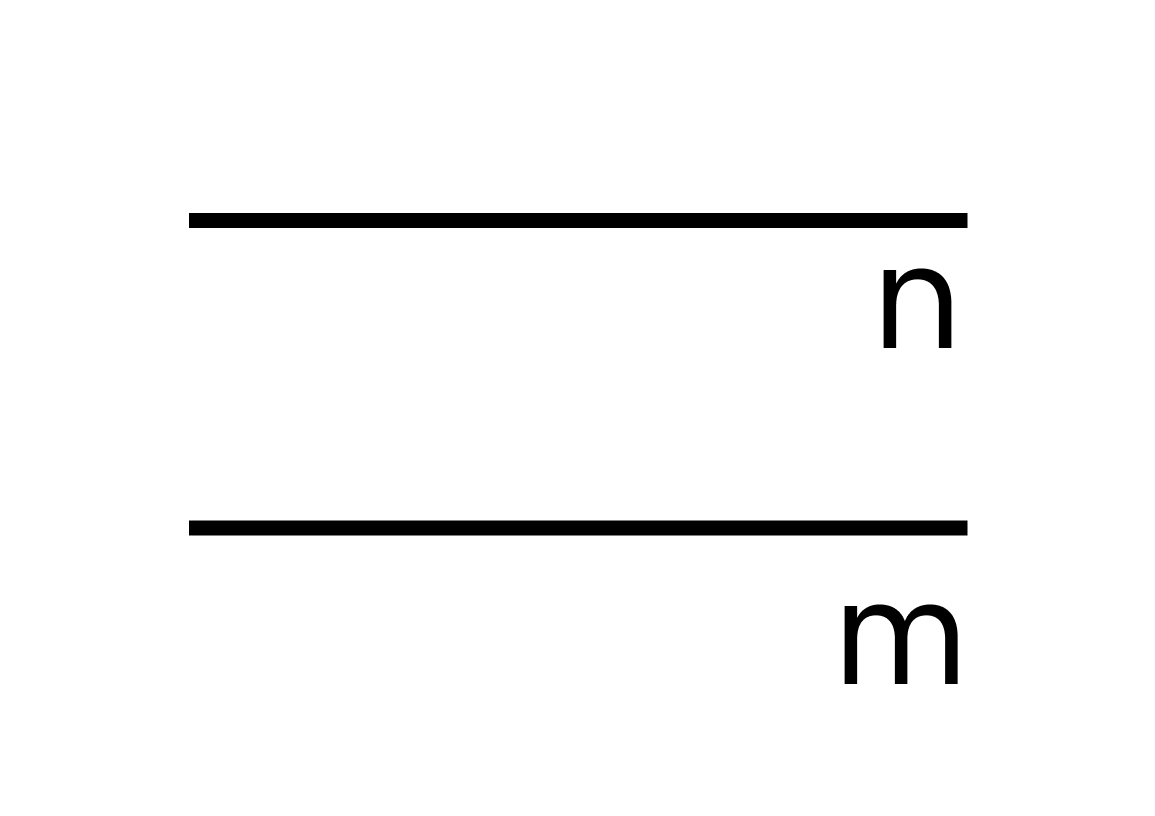
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
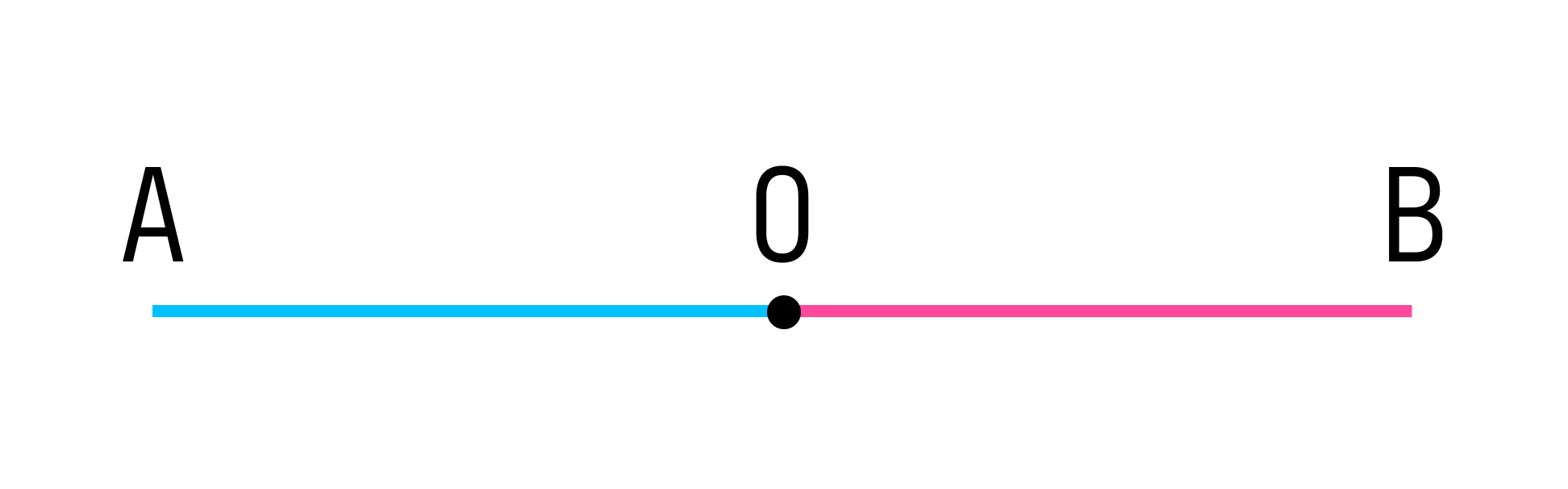
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
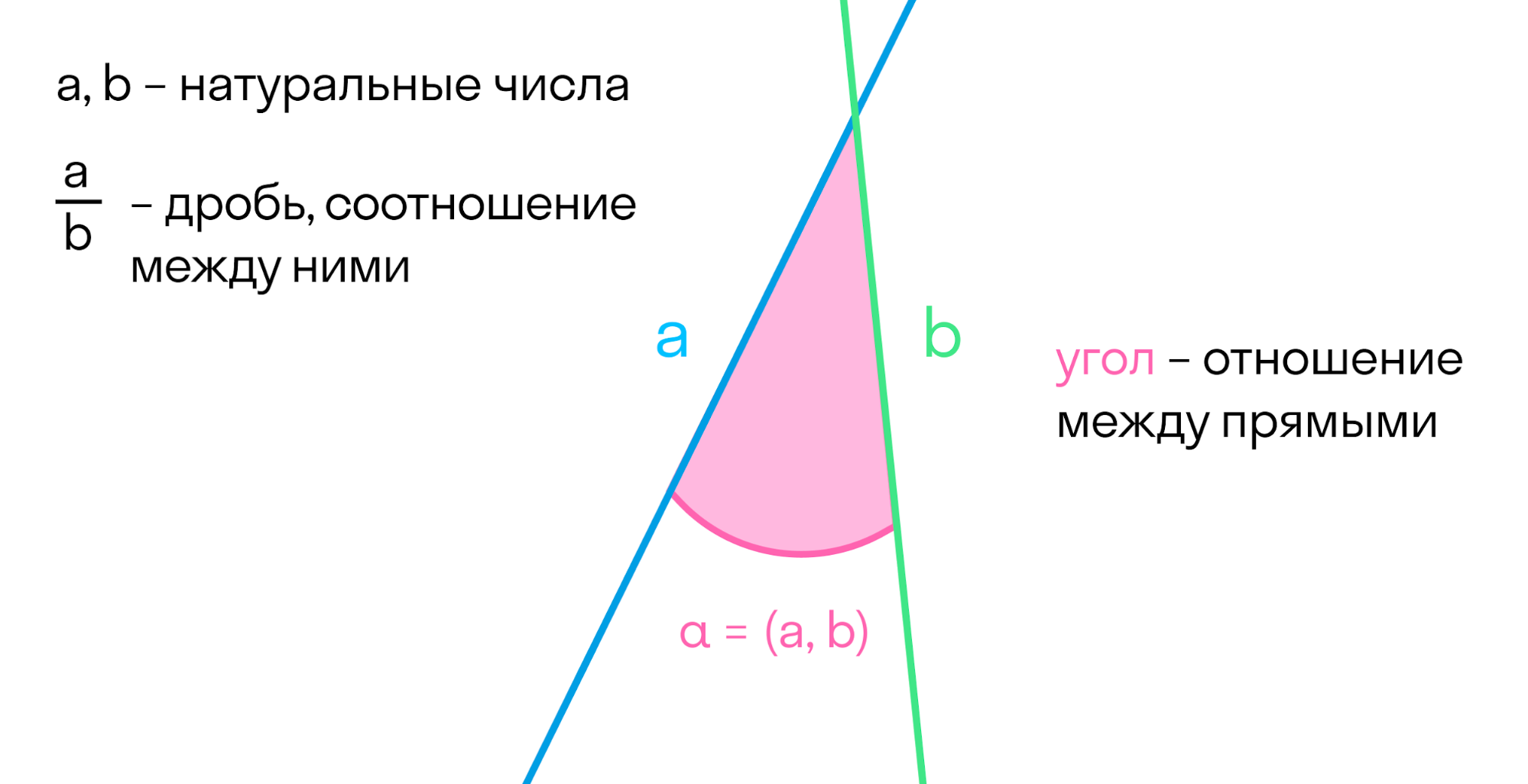
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
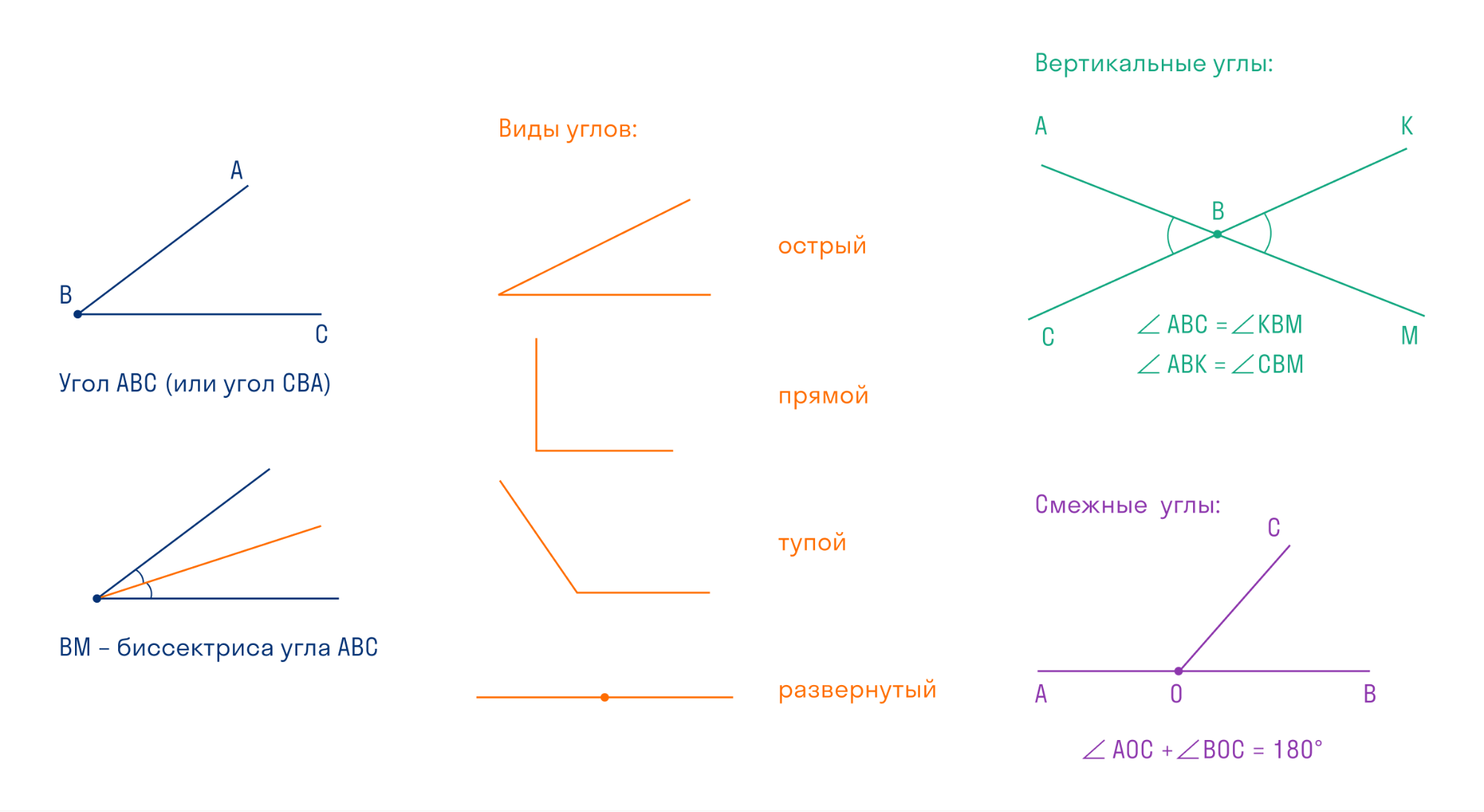
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
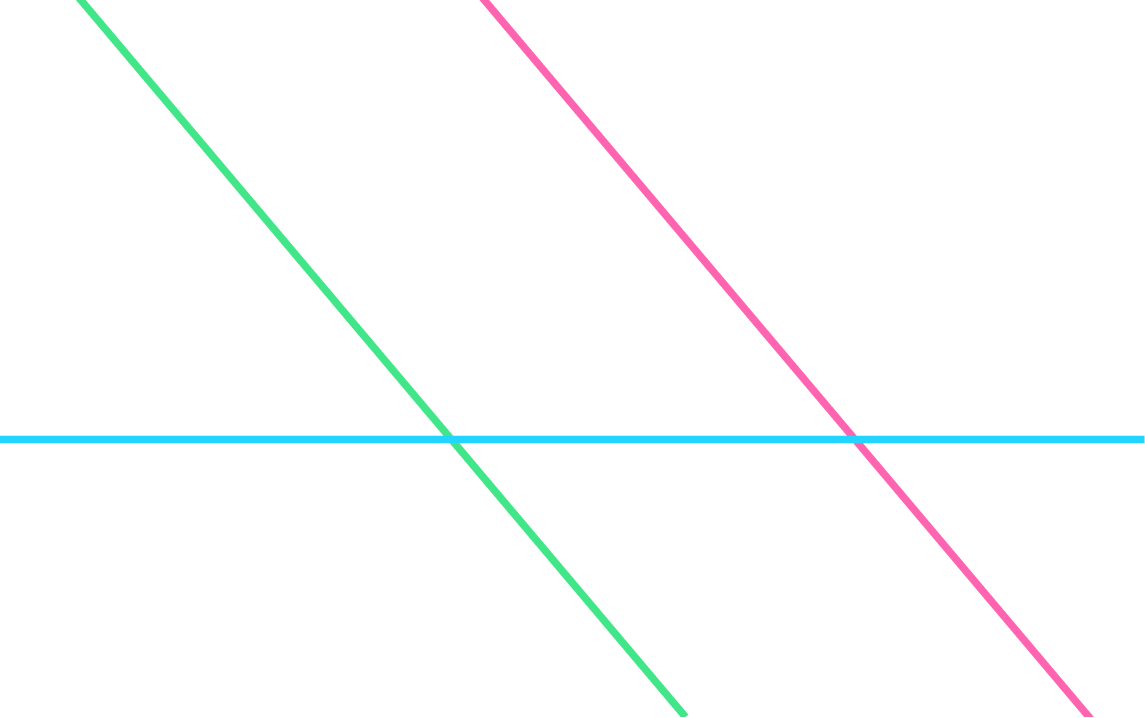
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
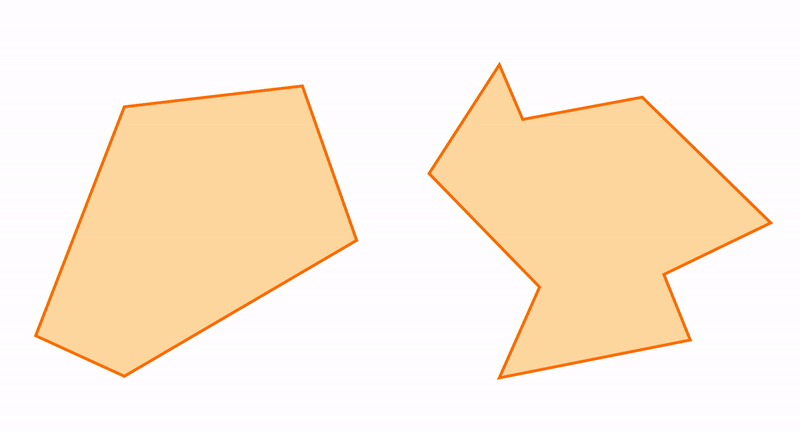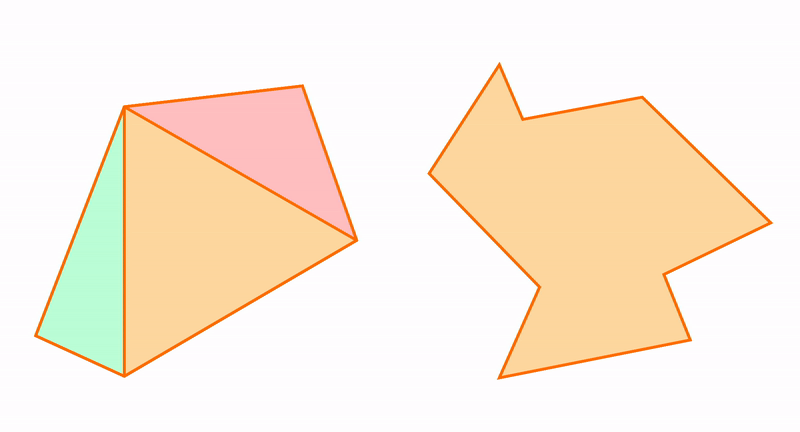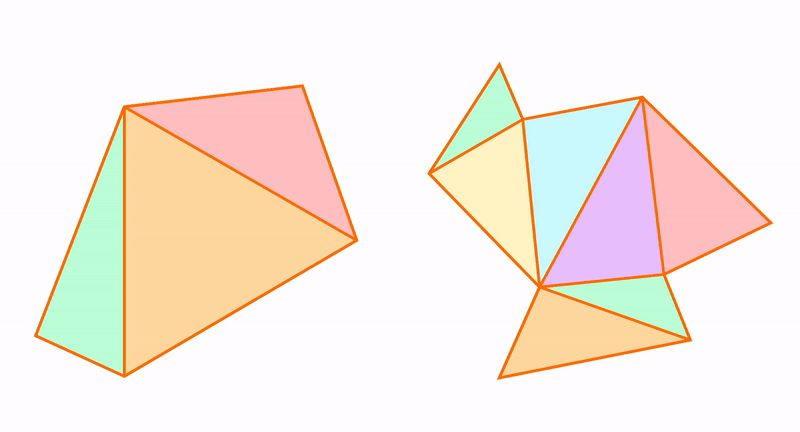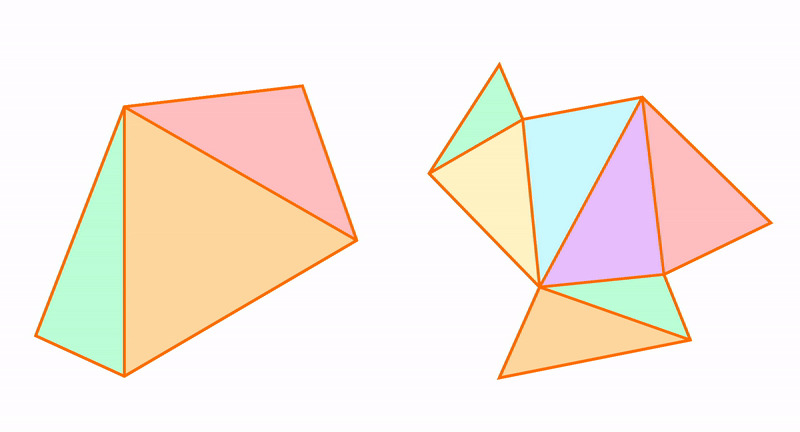
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
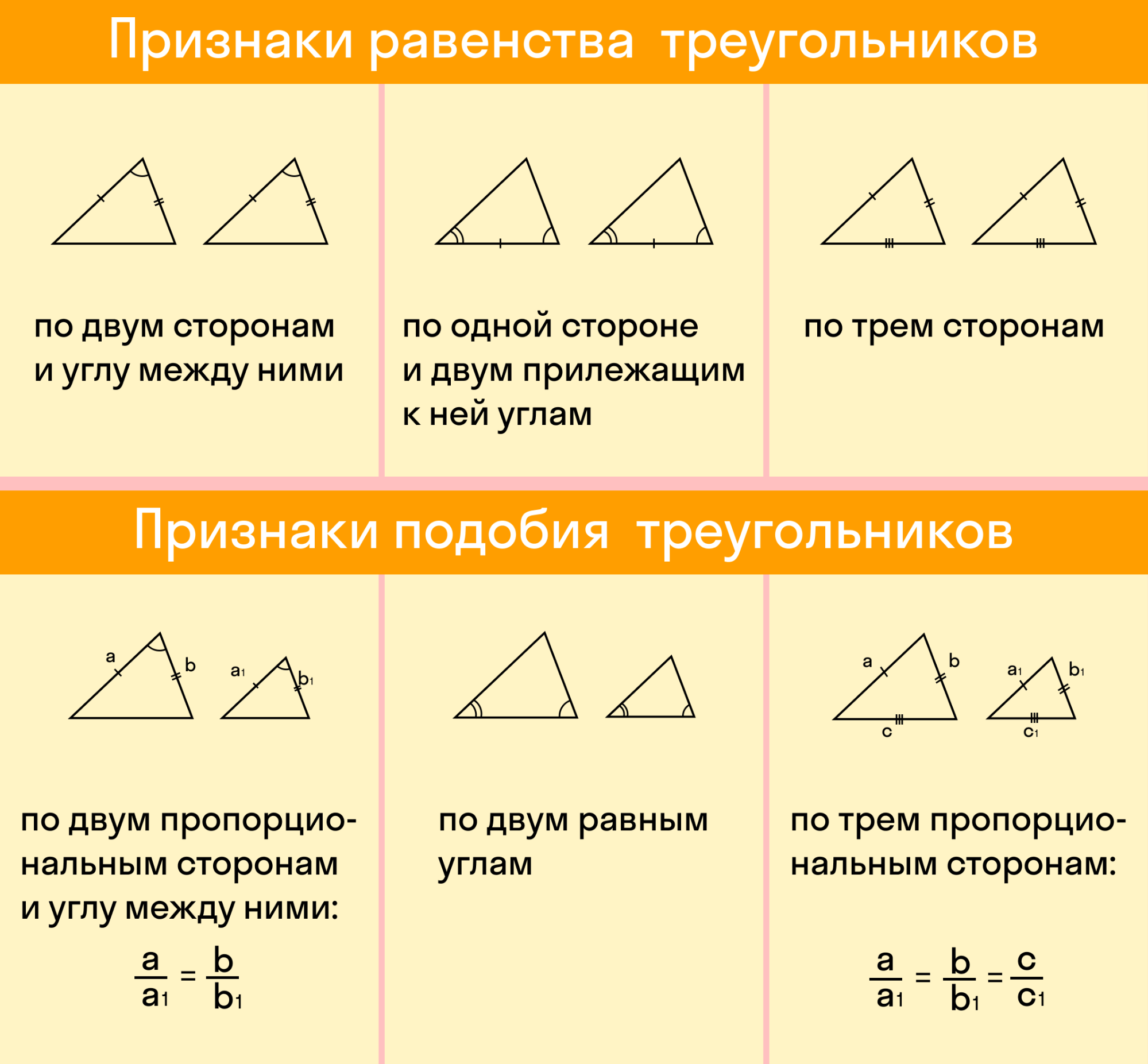
Первый признак равенства треугольников звучит так:
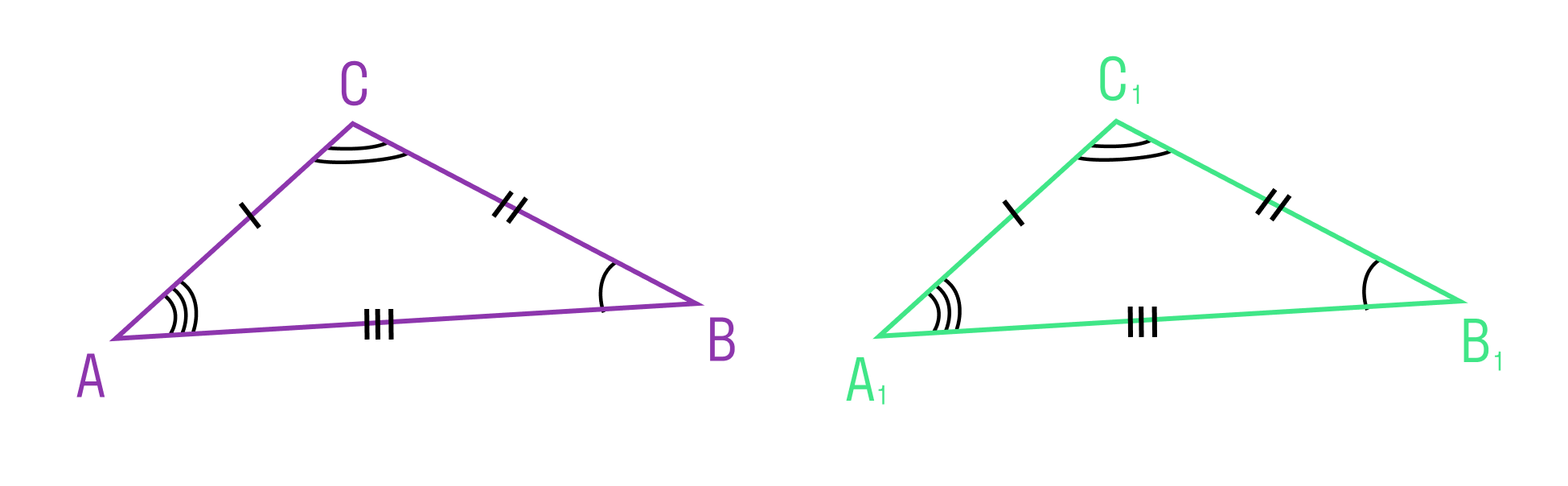
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Второй признак равенства треугольников
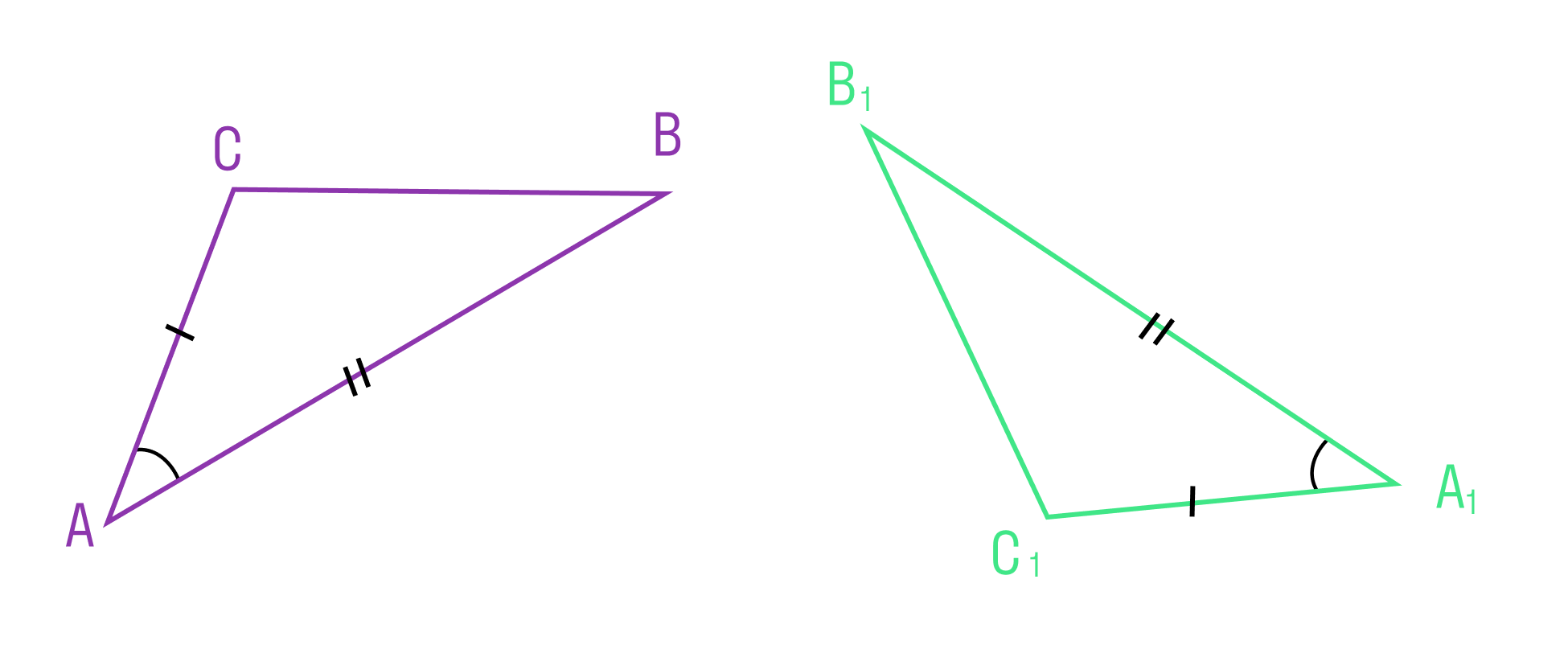
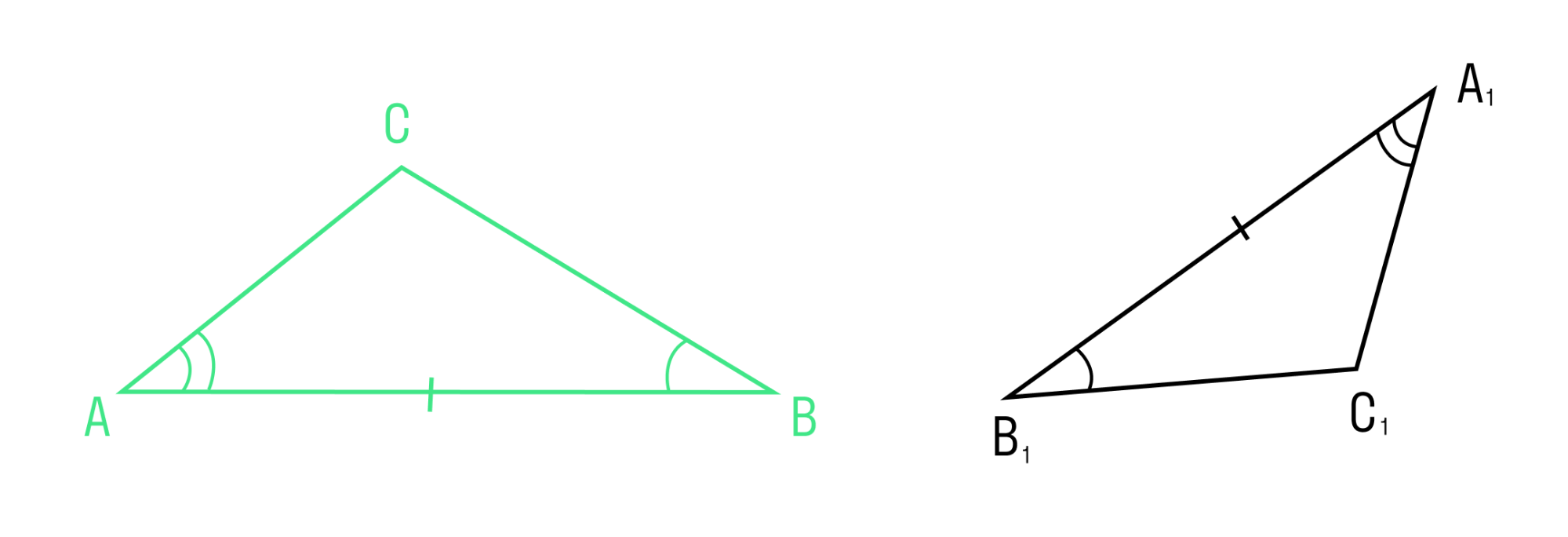
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников
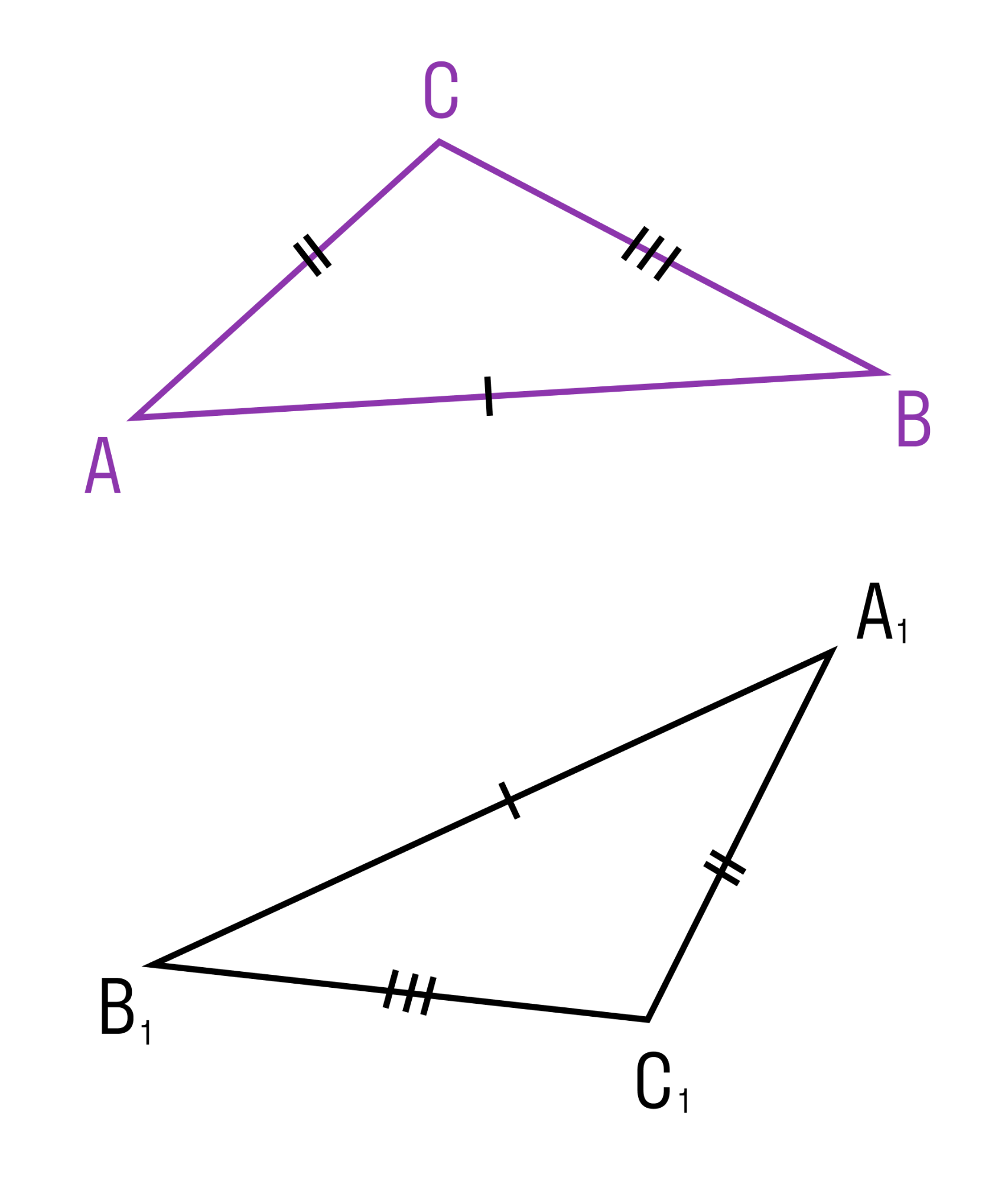
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
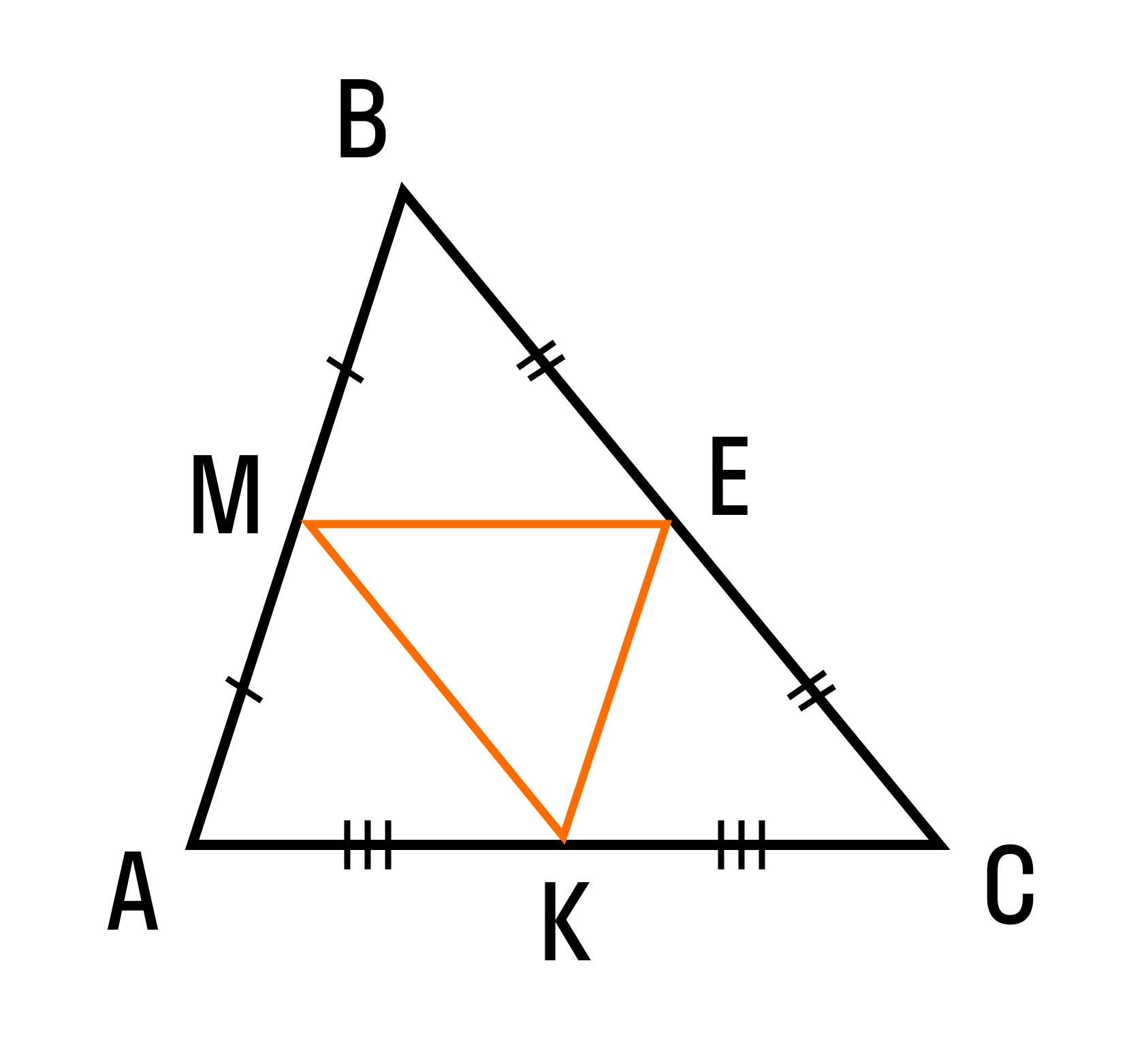
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
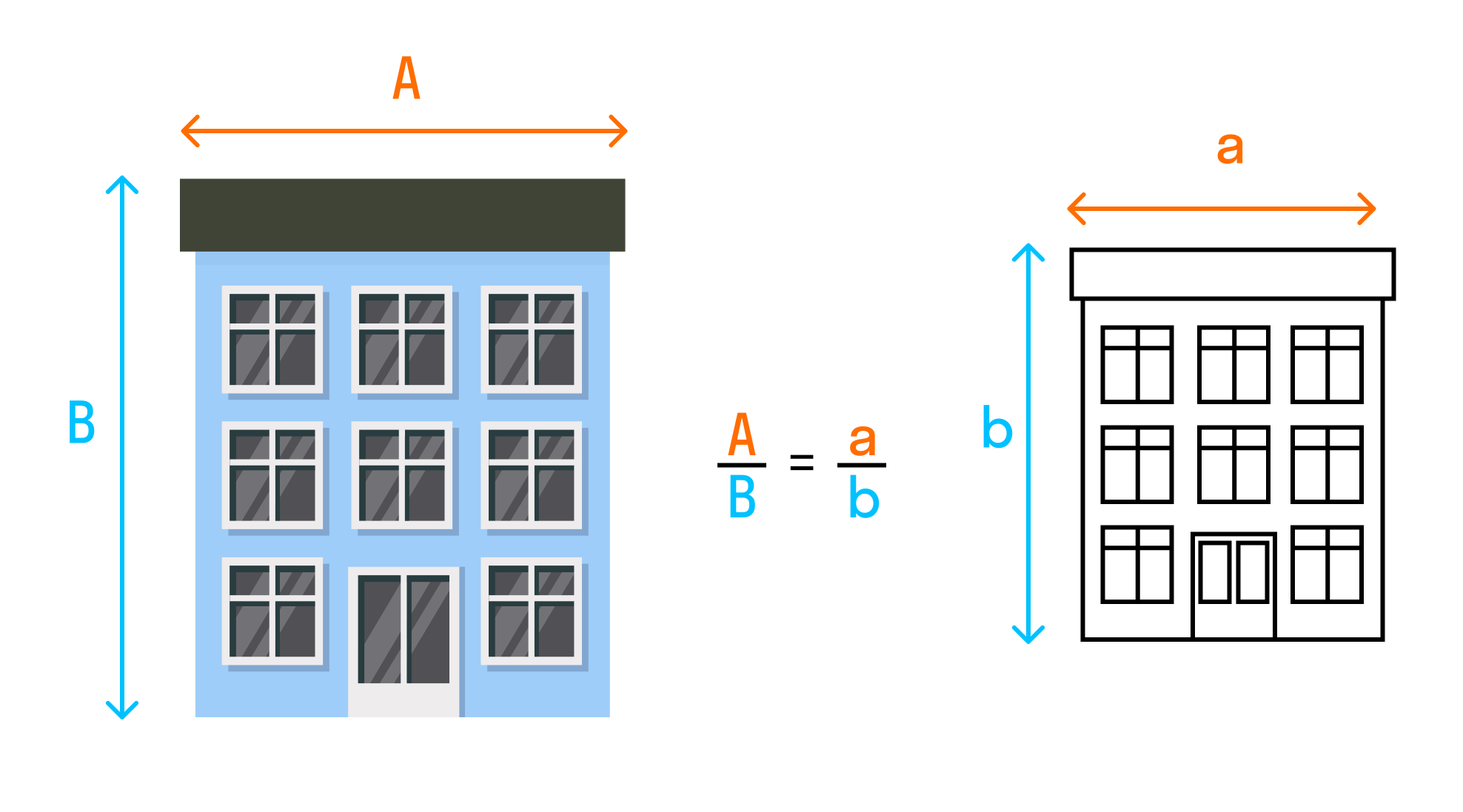
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
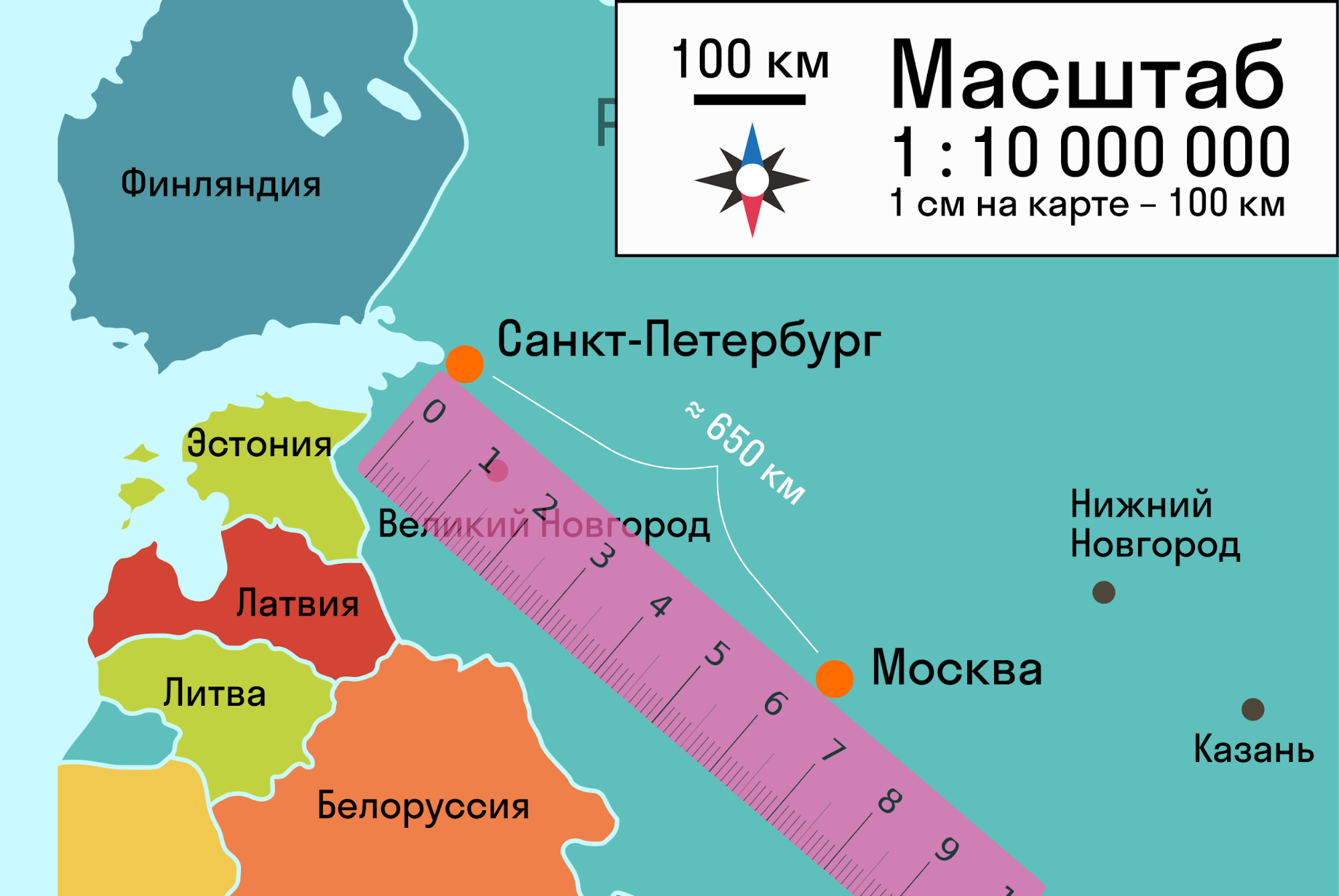
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
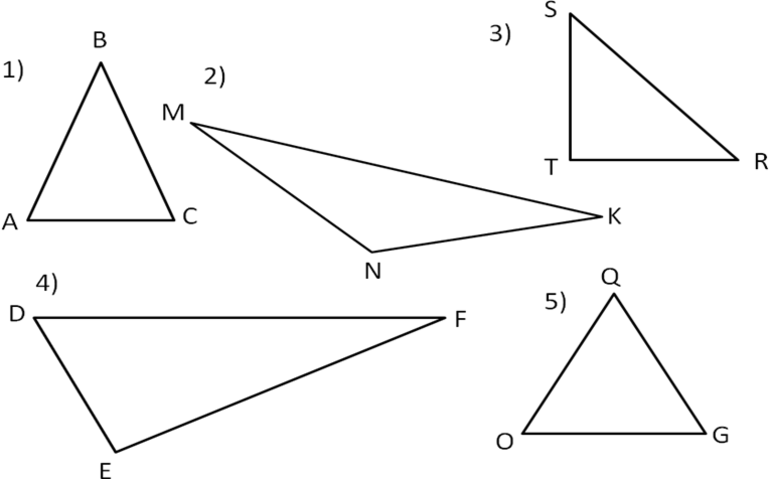
Для классификации треугольников можно использовать их типологию.
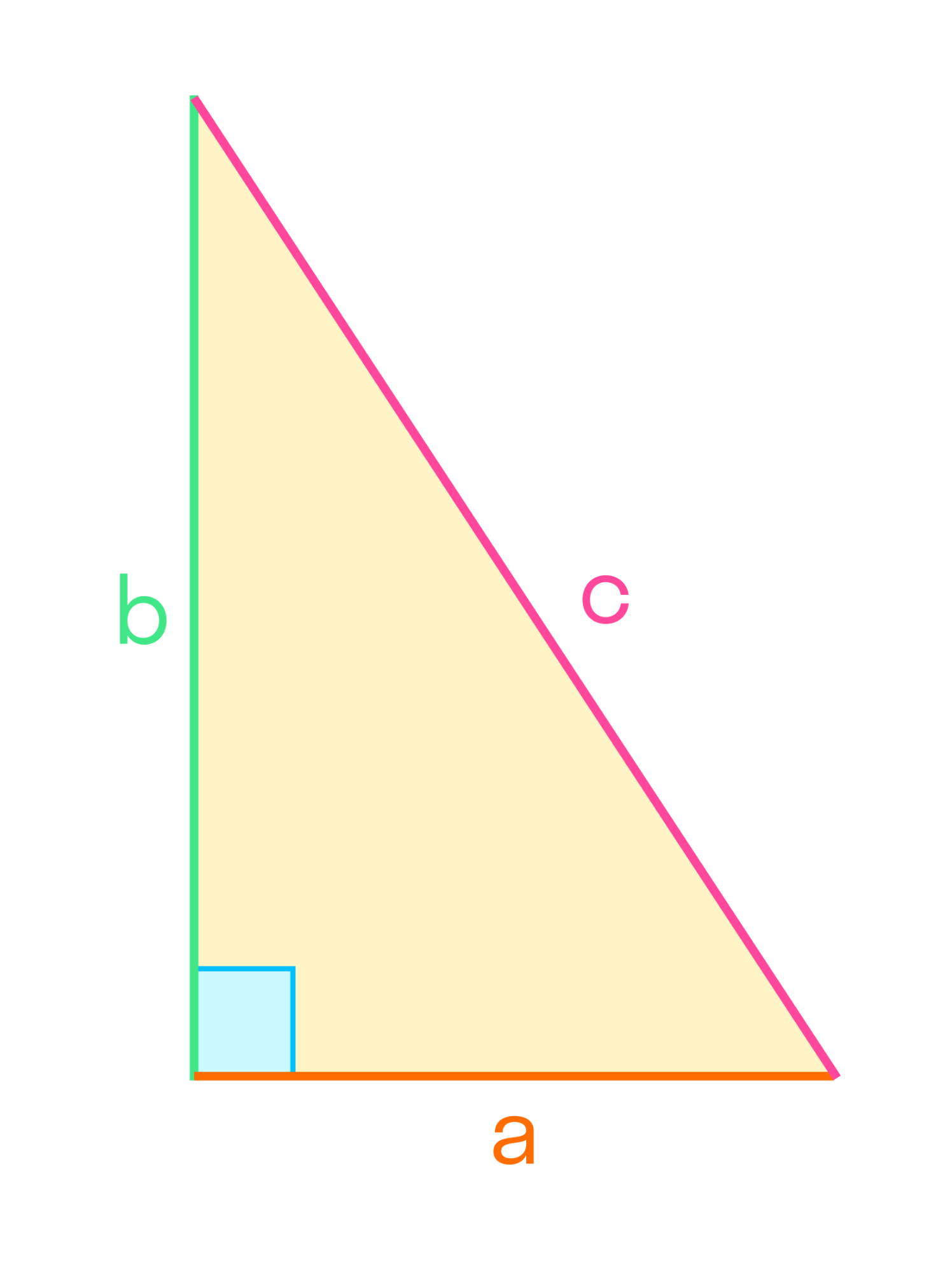
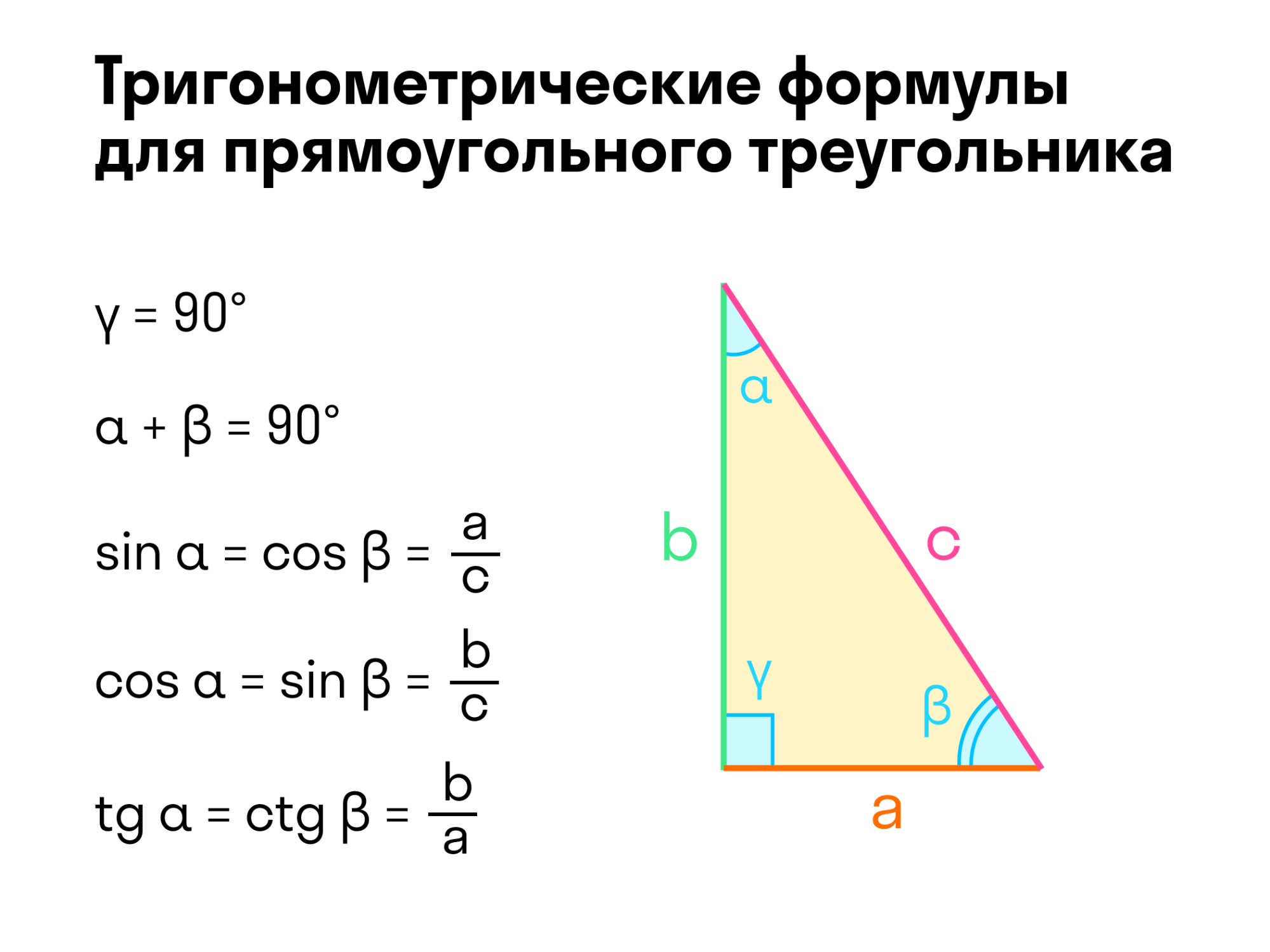
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
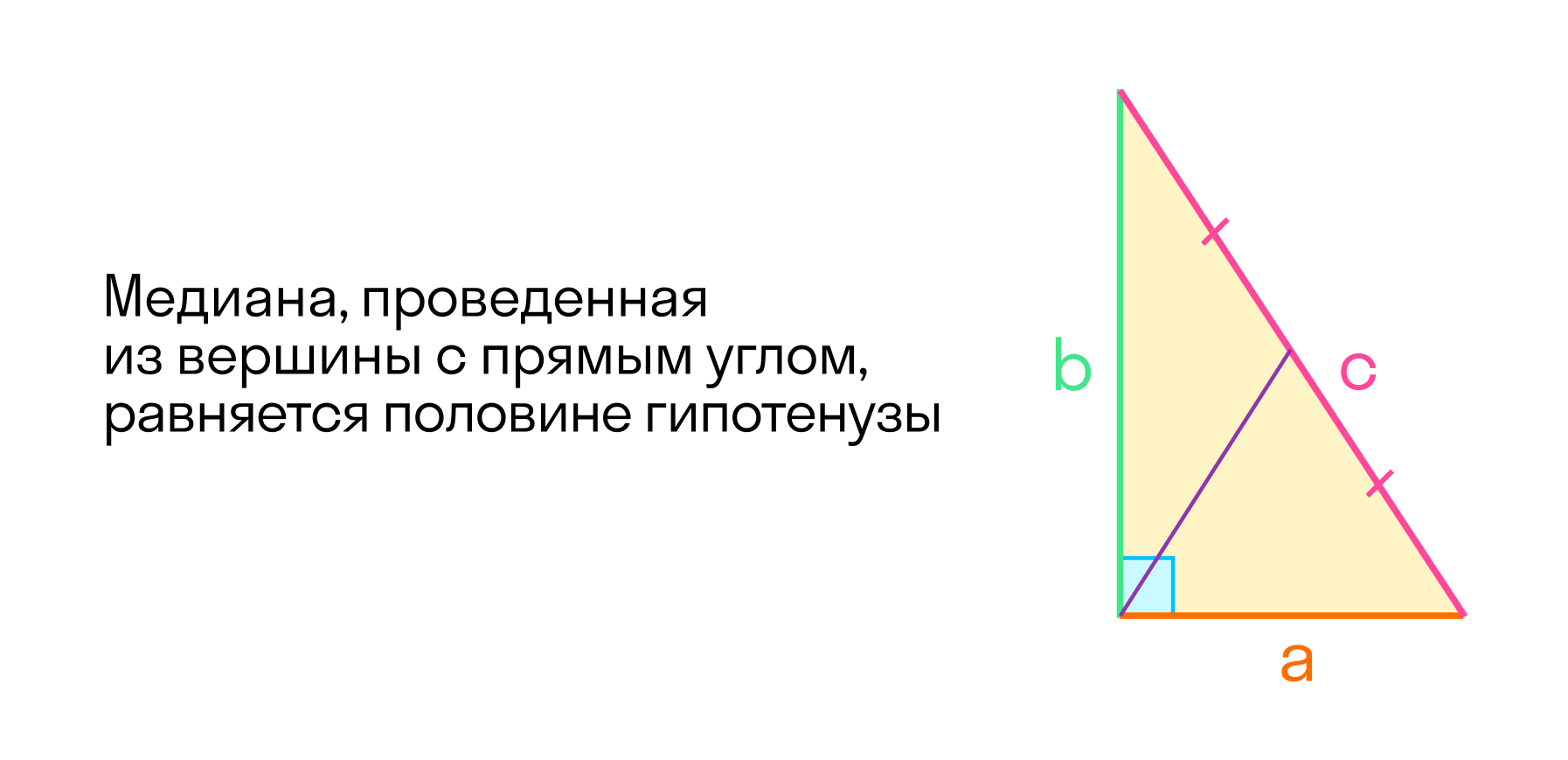
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
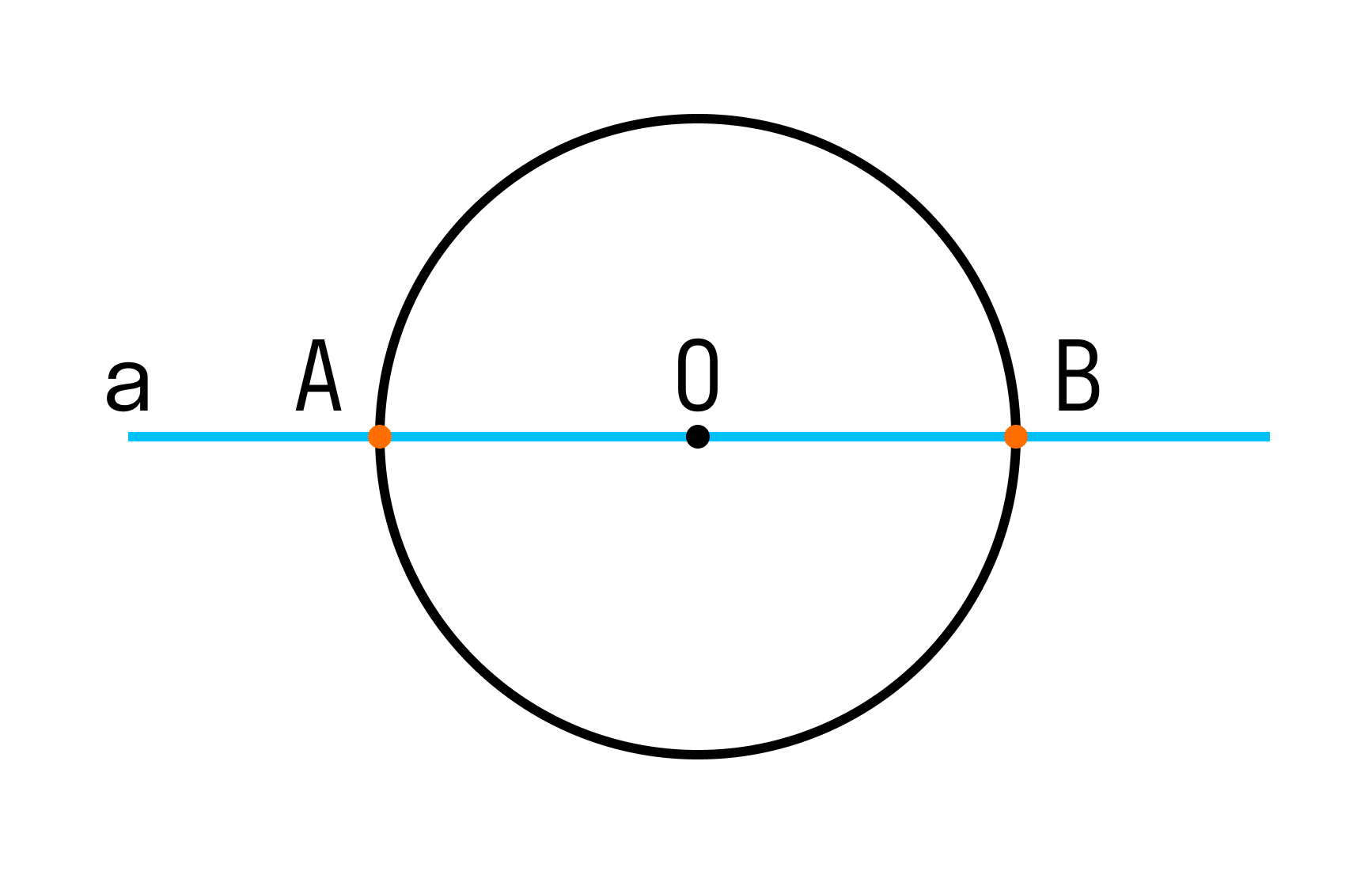
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
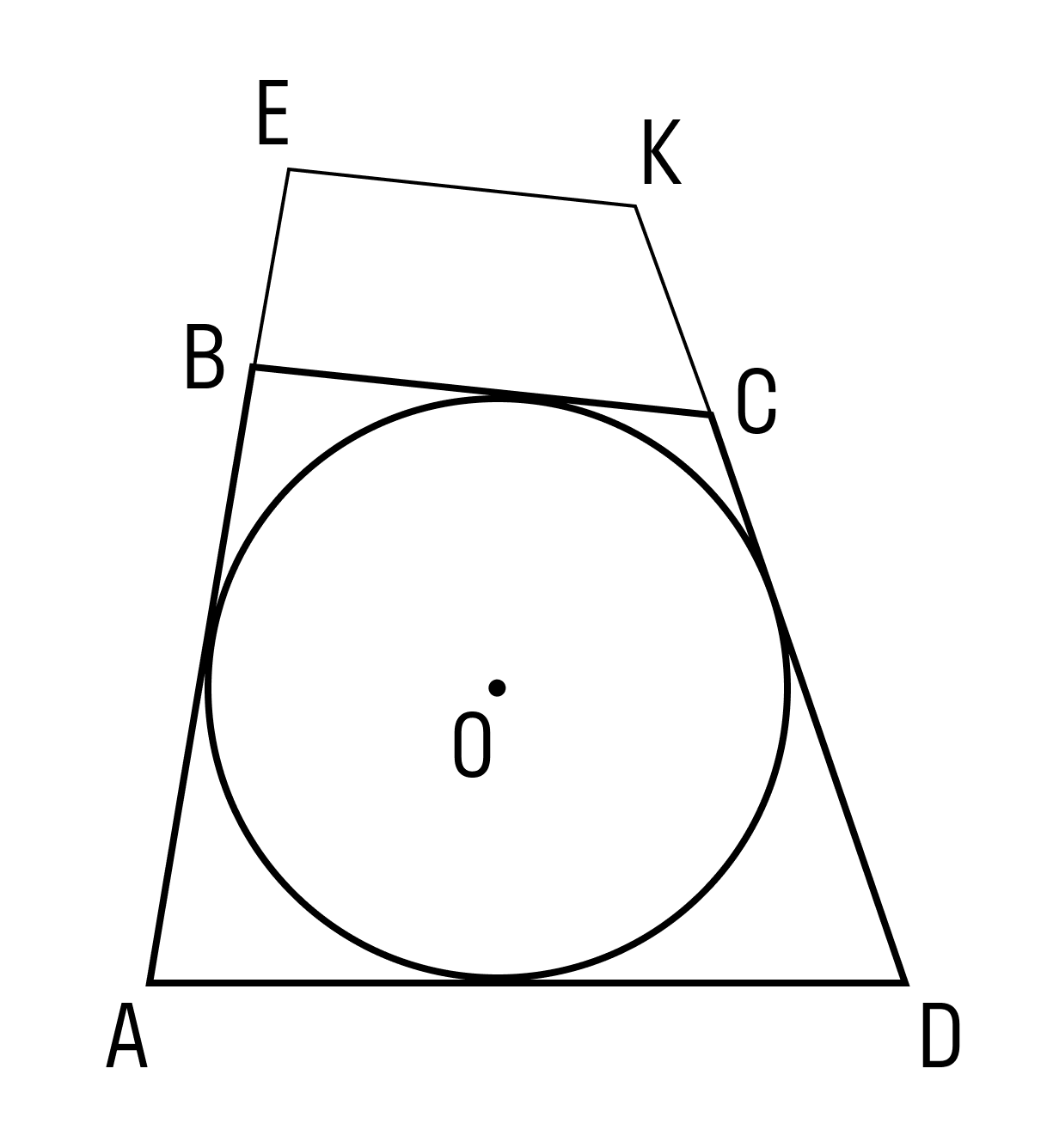
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
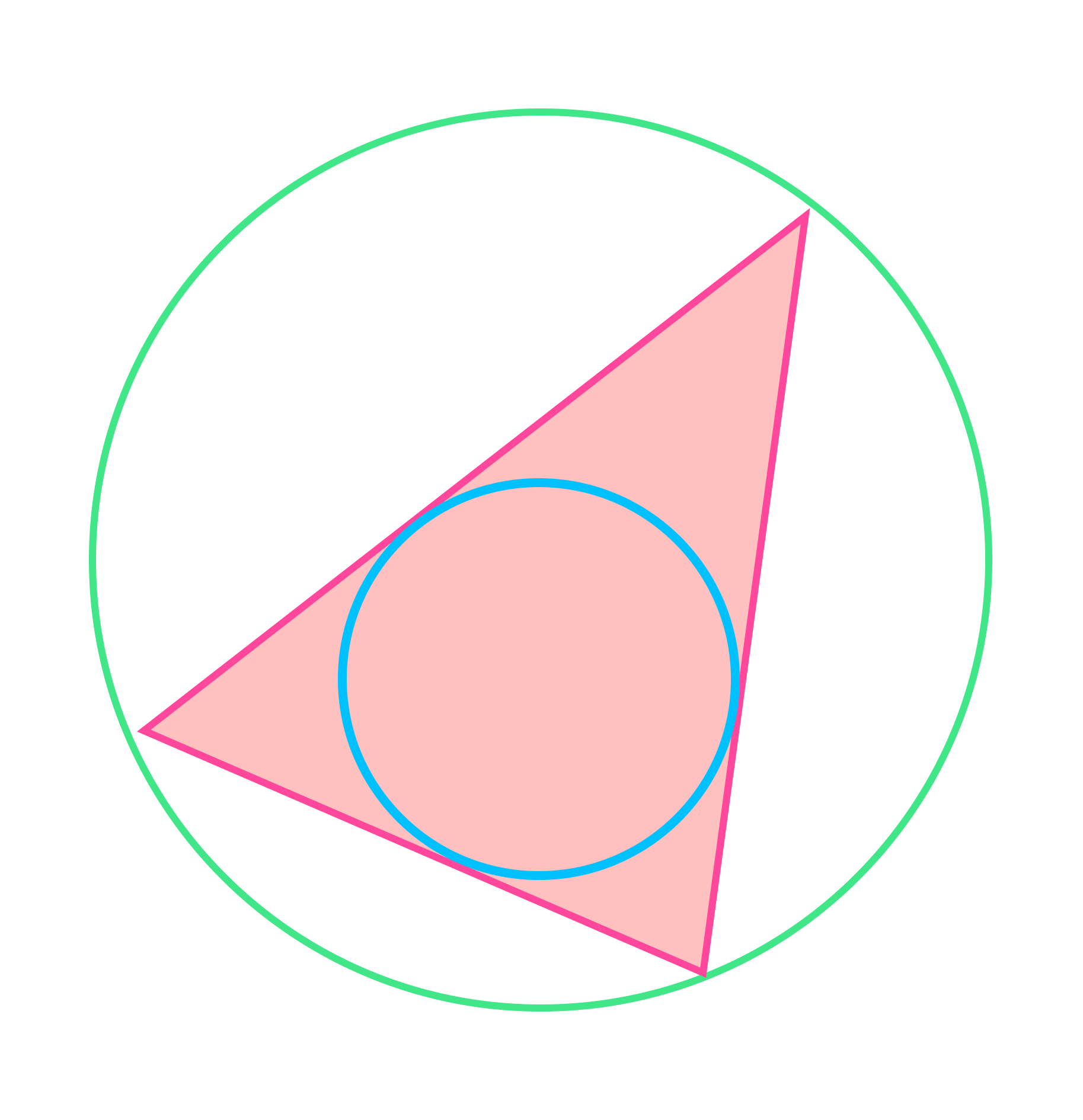
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.