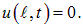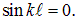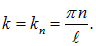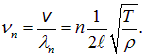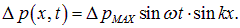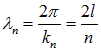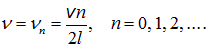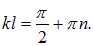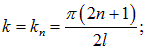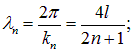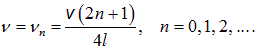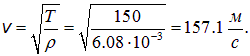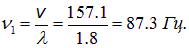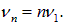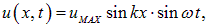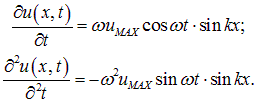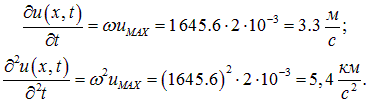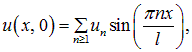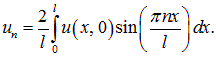Что такое гармоника в физике

ГАРМОНИКА

Смотреть что такое «ГАРМОНИКА» в других словарях:

ГАРМОНИКА — (лат., от греч. harmonia согласие, созвучие). Музыкальный инструмент, состоящий из ящика, в котором располагается валик с колокольчиками, звук извлекается посредством клавиш; изобретен Делавалем и усовершенствован Франклином; впоследствии стали… … Словарь иностранных слов русского языка

ГАРМОНИКА — ГАРМОНИКА, гармоники, жен. (нем. Harmonika). 1. Духовой музыкальный инструмент, состоящий из двух дощечек с клавиатурой, соединенных раздвижными мехами. «Гармоника, гармоника, эй, пой, визжи и жги!» А.Блок. 2. Раздвижной складчатый кожух,… … Толковый словарь Ушакова

гармоника — гармония, гармонь, гармошка; колебание, частота; концертина, субгармоника, хромка, инструмент, фисгармония, лушэн, тальянка, аккордеон, баян Словарь русских синонимов. гармоника / однорядовая: тальянка ) Словарь синонимов русского языка.… … Словарь синонимов

гармоника — Гармоническая составляющая периодических колебаний. Примечание Частоты гармоник кратны частоте анализируемых периодических колебаний. [ГОСТ 24346 80] гармоника Гармонический сигнал с амплитудой и начальной фазой, равными соответственно значениям… … Справочник технического переводчика

ГАРМОНИКА — ГАРМОНИКА, и, жен. 1. Духовой язычковый музыкальный инструмент подвижные меха с двумя дощечками, снабжёнными клавиатурой. 2. перен. Ряд частых расходящихся параллельных складок (разг.). Сложить бумагу гармоникой. • Губная гармоника музыкальный… … Толковый словарь Ожегова

гармоника — периодических колебаний; гармоника Каждое слагаемое периодических колебаний, представляемых в виде суммы гармонических колебаний … Политехнический терминологический толковый словарь

ГАРМОНИКА — (гармонь) (от греч. harmonikos созвучный стройный), клавишно пневматический духовой музыкальный инструмент с проскакивающими язычками. Изобретена немецким мастером К. Ф. Л. Бушманом (1822). Распространилась у многих народов Европы, в т. ч. в… … Большой Энциклопедический словарь

гармоника — и, ж. harmonique. устаревающ. Батарея отопления. Глупые ненужные предметы нелепой комнаты каждый посылали ему какой либо очередной упрек, словно только затем эти шифоньерки, кронштейны и пуфы и были сюда понапиханы, подтяжки висели на гармонике… … Исторический словарь галлицизмов русского языка

ГАРМОНИКА — синусоидальная (гармоническая) составляющая периодического процесса с частотой, кратной его основной частоте колебания … Большая политехническая энциклопедия

Источник

гармоника

гармоника
Гармоническая составляющая периодических колебаний.
Примечание
Частоты гармоник кратны частоте анализируемых периодических колебаний.
[ГОСТ 24346-80]

Из курса математики известно, что любую несинусоидальную функцию f(ωt), удовлетворяющую условию Дирихле можно представить в виде суммы постоянной величины и бесконечного ряда синусоидальных величин с кратными частотами.

Такие синусоидальные составляющие называются гармоническими составляющими или гармониками. Синусоидальная составляющая, период которой равен периоду несинусоидальной периодической величины, называется основной или первой гармоникой. Остальные составляющие синусоиды с частотами со второй по n-ую называют высшими гармониками.

Уровень каждой гармоники между 600 и 2000 Гц, не указанный выше, составляет 0,3 % от Uном.
[ГОСТ Р МЭК 61037-2001]

Тематики

Действия

Синонимы

Сопутствующие термины

Полезное

Смотреть что такое «гармоника» в других словарях:

ГАРМОНИКА — (лат., от греч. harmonia согласие, созвучие). Музыкальный инструмент, состоящий из ящика, в котором располагается валик с колокольчиками, звук извлекается посредством клавиш; изобретен Делавалем и усовершенствован Франклином; впоследствии стали… … Словарь иностранных слов русского языка

ГАРМОНИКА — ГАРМОНИКА, гармоники, жен. (нем. Harmonika). 1. Духовой музыкальный инструмент, состоящий из двух дощечек с клавиатурой, соединенных раздвижными мехами. «Гармоника, гармоника, эй, пой, визжи и жги!» А.Блок. 2. Раздвижной складчатый кожух,… … Толковый словарь Ушакова

гармоника — гармония, гармонь, гармошка; колебание, частота; концертина, субгармоника, хромка, инструмент, фисгармония, лушэн, тальянка, аккордеон, баян Словарь русских синонимов. гармоника / однорядовая: тальянка ) Словарь синонимов русского языка.… … Словарь синонимов

ГАРМОНИКА — ГАРМОНИКА, и, жен. 1. Духовой язычковый музыкальный инструмент подвижные меха с двумя дощечками, снабжёнными клавиатурой. 2. перен. Ряд частых расходящихся параллельных складок (разг.). Сложить бумагу гармоникой. • Губная гармоника музыкальный… … Толковый словарь Ожегова

гармоника — периодических колебаний; гармоника Каждое слагаемое периодических колебаний, представляемых в виде суммы гармонических колебаний … Политехнический терминологический толковый словарь

ГАРМОНИКА — (гармонь) (от греч. harmonikos созвучный стройный), клавишно пневматический духовой музыкальный инструмент с проскакивающими язычками. Изобретена немецким мастером К. Ф. Л. Бушманом (1822). Распространилась у многих народов Европы, в т. ч. в… … Большой Энциклопедический словарь

ГАРМОНИКА — (см. ОБЕРТОН). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия

гармоника — и, ж. harmonique. устаревающ. Батарея отопления. Глупые ненужные предметы нелепой комнаты каждый посылали ему какой либо очередной упрек, словно только затем эти шифоньерки, кронштейны и пуфы и были сюда понапиханы, подтяжки висели на гармонике… … Исторический словарь галлицизмов русского языка

ГАРМОНИКА — синусоидальная (гармоническая) составляющая периодического процесса с частотой, кратной его основной частоте колебания … Большая политехническая энциклопедия

Источник

Гармонические колебания

На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.

Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).

Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.

Пару слов о матчасти

Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания

Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:

где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:

ω=2 πf, где f — частота в Герцах.

Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.

Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал

Его сумма будет представлена следующей формулой:

Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:

Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.

Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.

Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)

Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.

Переходим к практическим упражнениям!

Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).

Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.

Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.

Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут

Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:

Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).

В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус

Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра

Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.

Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.

В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.

Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.

Пишем свой анализатор спектра

Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.

Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.

Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.

Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.

Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.

Для начала алокируем массивы:

Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).

Массив для быстрого преобразования Фурье должен представлять собой последовательность , где fft_size=1

Источник

Гармоники

На струне, закрепленной на одном конце, могут существовать колебания любых частот. Закрепим теперь второй конец струны в точке с координатой . Имеем то же решение (2.53), которое должно удовлетворять дополнительному граничному условию:

На струне длиной l, закрепленной на обоих концах, могут существовать только стоячие волны с волновыми векторами

Соответственно, длины волн будут

Иными словами, на длине струны должно укладываться целое число полуволн. Следовательно, закрепленная с обоих концов струна может колебаться только с определенными частотами:

Мы использовали здесь уравнение (2.2) для скорости волн на натянутой струне.

Из (2.58) видно, что частота колебаний повышается при:

Эти закономерности известны каждому, кто держал в руках хотя бы гитару. Колебания с низшей частотой (n = 1) называются основной (первой) гармоникой, с последующими частотами — высшими (второй, третьей и т. п.) гармониками.

Аналогичные граничные условия существуют и для колебаний воздуха в трубах духовых музыкальных инструментов. Соответственно, в их сигналах также присутствуют только вполне определенные частоты. Рассмотрим, например, органную трубу длиной l. Волна давления в ней также может быть описана уравнением вида (2.53):

Если труба открыта с обеих сторон, то давление на концах равно стационарному (атмосферному) и в точках х = 0, l. Отсюда получаем те же условия для волновых чисел

Если же труба открыта в точке х = 0 и закрыта на другом конце (х = l), то на закрытом конце смещение частиц равно нулю, а давление достигает максимума или минимума:

Отсюда следуют несколько иные соотношения:

Первая гармоника для такой трубы возбуждается на частоте

что в два раза меньше частоты

первой гармоники полностью открытой трубы.

Пример 3. Нейлоновая гитарная струна имеет линейную плотность массы 7.2 г/м и натянута с силой 150 Н. Длина струны 90 см. Определим, каковы четыре низшие частоты, извлекаемые на такой струне?

Скорость волны на струне равна

Наибольшая длина стоячей волны в струне равна м. Отсюда находим самую низкую частоту:

(Эта частота соответствует ноте «фа» большой октавы.)

Следующие частоты являются целыми кратными n₁:

Отсюда следует: n₁ = 2·87.3 = 174.6 Гц («фа» малой октавы), n₃ = 3·87.3 = 261.9 Гц («до» первой октавы) и n₁ = 4·87.3 = 349.2 Гц («фа» первой октавы).

Пример 4. Струна звучит на ноте «до» первой октавы. Максимальное отклонение точек струны от положения равновесия равно и_тах = 2 мм. Найдем максимальную скорость и ускорение точек струны.

Закон колебания струны имеет вид (ср. (2.53)):

откуда находим скорость и ускорение точек струны:

По условию (см. пример 3.). Максимальные значения скорости и ускорения равны:

Сложение гармоник

Выше мы уже занимались сложением колебаний, и теперь нам предстоит проделать то же самое, но для каждой точки колеблющейся струны.

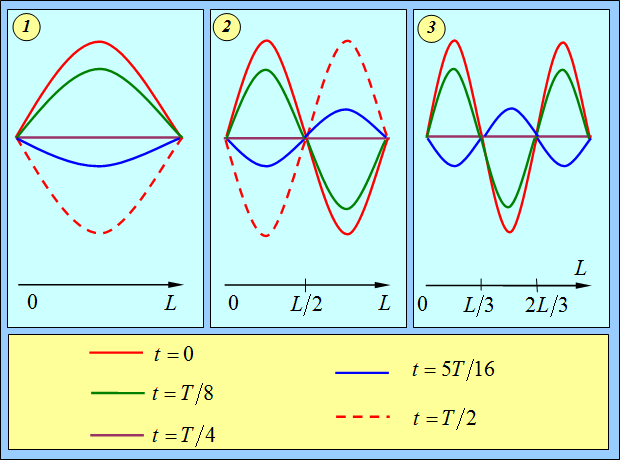
Движение струны при возбуждении основной (первой) гармоники, показано на рис. 2.10–1. В начальном положении (линия отмечена красным цветом) точки струны имеют максимальное отклонение от положения равновесия. Под действием силы упругости они начинают двигаться (на рисунке – вертикально вниз), и форма струны через 1/8 периода показана линией зеленого цвета. Через четверть периода струна приходит в положение равновесия (линия черного цвета), но ее элементы имеют некоторые скорости, и потому в положении равновесия не задерживаются. Еще через 1/16 периода они оказываются в положении, показанном линией синего цвета, а через половину периода струна снова приобретает максимальное отклонение (пунктирная линия красного цвета), но в другую сторону, после чего процесс повторяется в обратном направлении. Так происходит колебание в стоячей волне, соответствующее первой гармонике, частоту которой мы обозначаем n₁.

Рис. 2.10. Колебания струны:
1 – первая гармоника; 2 – вторая гармоника; 3 – третья гармоника;

Но на струне, как мы уже знаем, могут возникать колебания и других гармоник. Вторая гармоника показана на том же рис. 2.10–2. Использование тех же обозначений позволяет не описывать процесс колебаний столь же детально. Заметим, что в этом случае имеется одна неподвижная точка (ее называют узлом) в середине струны. Поскольку узел все равно не движется, можно представить себе, что мы закрепили среднюю точку. И тем самым, не изменив частоты издаваемого звука, в два раза укоротили струну. Стало быть, частота колебаний ровно в два раза превышает частоту основной гармоники: 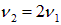. Этот результат мы уже получали другим способом.

На рис. 2.10–3 показаны колебания той же струны при возбуждении третьей гармоники. Здесь уже существует два узла, и издаваемый звук соответствует основному колебанию струны, укороченной в три раза (или, что то же самое, второй гармонике струны, длина которой составляет 2/3 исходной): .

Колебания струны для первых трех гармоник показаны на рис. 2.11.

Рис. 2.11. Колебания струны для первых трех гармоник

На обсуждавшихся рисунках гармоники показаны без учета их амплитуд, то есть без учета их относительного вклада. На самом деле вклад гармоник может быть различным, так что в общем случае результирующее колебание получается сложением всех гармоник, каждая из которых представлена уравнением, аналогичным (2.59):

Здесь мы уже учли, что частоты и волновые числа принимают дискретный ряд значений; коэффициенты 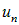– это амплитуды соответствующих гармоник. Заметим, что в множителе с зависимостью от времени мы заменили синус косинусом, то есть сдвинули точку отсчета времени. Теперь в момент t = 0 скорости всех точек струны равны нулю.

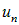
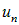
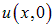
На практике приходится решать обратную задачу: находить коэффициенты по известному результирующему колебанию. Численные значения зависят от способа возбуждения струны, например, от ее начальной формы . Если нам задана функция , то для нее из (2.62) следует разложение:

которое известно в математике как разложение в ряд Фурье. Там же доказывается теорема, что коэффициенты и_п однозначно восстанавливаются по функции :

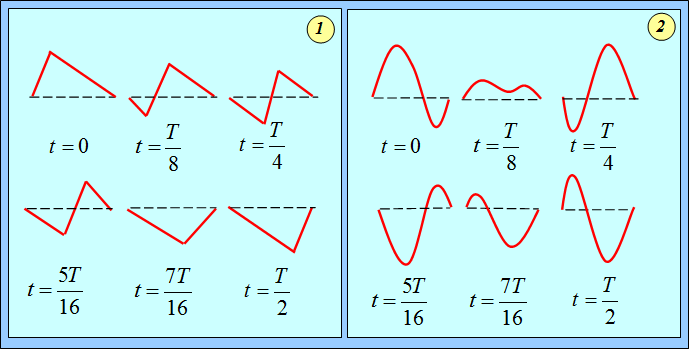
От величины примеси высших гармоник зависит форма колеблющейся струны. На рис. 2.12 показан вид колеблющейся струны в разные моменты времени при двух способах ее возбуждения. В обоих случаях струне придается некая начальная форма, после чего она отпускается «на свободу» (оставаясь закрепленной на концах, разумеется).

Рис. 2.12. Форма колеблющейся струны в различные моменты времени при разных формах струны в начальном состоянии:
1 – струна оттянута на расстоянии 0.1 ее длины; 2 – струне придана кусочно-синусоидная форма.

Мы рассматриваем два случая:

Второй пример носит явно модельный характер и дан для сравнения. Надо сказать, что придание струне какой-то начальной формы — не единственный способ возбуждения колебаний. Можно, например, задать начальное распределение скоростей (как происходит, скажем, в фортепиано, где молоточек ударяет по струне, находящейся в положении равновесия).

Мы все же ограничимся двумя описанными случаями. На рис. 22.6 показаны положения точек струны за половину периода колебаний основной гармоники, после чего процесс повторяется в обратном направлении. За время, равное периоду колебаний Т₁ первой гармоники, струна возвращается в исходное положение. Если струна настроена на ноту «до» первой октавы, то Т₁ = 3.82 мс.

Источник