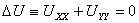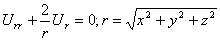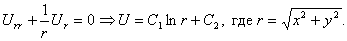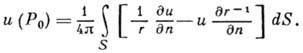Что такое гармоническая функция
Лекция 7. Гармонические функции и их свойства
Рассмотрим уравнение Лапласа на плоскости
Уравнение (33) при переходе к полярным координатам преобразуется к виду
Рис 14 Рис 14.1
Если в пространстве перейти к сферическим координатам
то уравнение (34) примет вид
Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим
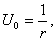
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U0 является гармонической всюду в пространстве, кроме начала координат 0.
Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:
Выбирая С1=-1 и С2=0, будем иметь функцию 
Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен
Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.
Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (хo,уo) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть
При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)
Если в этой формуле положить ρ=0, то получится формула (35).
Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 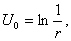(см. рис.15.1):
Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:
В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.
Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (хо, уо), то эта функция гармоническая в D. Из формулы (37) получается:
Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:
Применим это неравенство к формуле (37):
Что и требовалось доказать.
Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.
Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (xo, уo) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству
Из неравенства Харнака следует теорема Лиувилля.
Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.
Воспользуемся неравенством Харнака
Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим
то есть Теорема Лиувилля доказана.
Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.
а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть
б) ее среднему значению в шаре D, то есть
Гармоническая функция
Гармони́ческая фу́нкция — вещественная функция 
, определенная и дважды непрерывно дифференцируемая на евклидовом пространстве 
(или его открытом подмножестве), удовлетворяющая уравнению Лапласа:
Например, гармонической функцией является электростатический потенциал в точках, где отсутствует заряд.
Содержание
Свойства
Принцип максимума
Функция U, гармоническая в области , достигает своего максимума и минимума только на границе 
. Таким образом, гармоническая функция не может иметь во внутренней точке области локального экстремума, за исключением тривиального случая постоянной в функции. Однако функция может быть неопределена на границе, поэтому правильнее сказать 
Теорема Лиувилля
Гармоническая функция, определённая на 
и ограниченная сверху или снизу, постоянна.
Свойство среднего
Если функция 
гармонична в некотором шаре 
с центром в точке 
, то её значение в точке равно её среднему значению по границе этого шара или по шару:
где 
— объём шара и 
— площадь его границы. Обратно, любая функция, обладающая свойством среднего в некоторой области, является в этой области гармонической.
Дифференцируемость
Функция, гармоническая в области, бесконечно дифференцируема в ней.
Литература
См. также
Полезное
Смотреть что такое «Гармоническая функция» в других словарях:
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция, непрерывная со своими вторыми производными в области G и удовлетворяющая в G Лапласа уравнению =0. Г. ф. возникают при решении задач электростатики, теории тяготения, гидродинамики несжимаемой жидкости, теории упругости и др. Г. ф.… … Физическая энциклопедия
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция нескольких переменных, непрерывная в некоторой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному Лапласа уравнению … Большой Энциклопедический словарь
гармоническая функция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN harmonic function … Справочник технического переводчика
гармоническая функция — функция нескольких переменных, непрерывная в некоторой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному уравнению Лапласа. * * * ГАРМОНИЧЕСКАЯ ФУНКЦИЯ ГАРМОНИЧЕСКАЯ ФУНКЦИЯ, функция… … Энциклопедический словарь
гармоническая функция — harmoninė funkcija statusas T sritis automatika atitikmenys: angl. harmonic function vok. harmonische Funktion, f rus. гармоническая функция, f pranc. fonction harmonique, f … Automatikos terminų žodynas
гармоническая функция — harmoninė funkcija statusas T sritis fizika atitikmenys: angl. harmonic function vok. harmonische Funktion, f rus. гармоническая функция, f pranc. fonction harmonique, f … Fizikos terminų žodynas
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция неск. переменных, непрерывная в нек рой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному ур нию Лапласа … Естествознание. Энциклопедический словарь
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — действительная функция заданная в области Dевклидова пространства имеющая в Dнепрерывные частные производные 1 го и 2 го порядков и являющаяся решением Лапласа уравнения где декартовы прямоугольные координаты точки х. Иногда это определение… … Математическая энциклопедия
Гармоническая функция — (от лат. functio осуществление, исполнение, деятельность) роль, значение аккорда в гармонич. системе мажора и минора, вообще в любой гармонической системе. Г. ф. представляет собой проявление ладовой функции (см. Функции ладовые) в… … Музыкальная энциклопедия
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ
Полезное
Смотреть что такое «ГАРМОНИЧЕСКАЯ ФУНКЦИЯ» в других словарях:
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция нескольких переменных, непрерывная в некоторой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному Лапласа уравнению … Большой Энциклопедический словарь
гармоническая функция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN harmonic function … Справочник технического переводчика
гармоническая функция — функция нескольких переменных, непрерывная в некоторой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному уравнению Лапласа. * * * ГАРМОНИЧЕСКАЯ ФУНКЦИЯ ГАРМОНИЧЕСКАЯ ФУНКЦИЯ, функция… … Энциклопедический словарь
гармоническая функция — harmoninė funkcija statusas T sritis automatika atitikmenys: angl. harmonic function vok. harmonische Funktion, f rus. гармоническая функция, f pranc. fonction harmonique, f … Automatikos terminų žodynas
гармоническая функция — harmoninė funkcija statusas T sritis fizika atitikmenys: angl. harmonic function vok. harmonische Funktion, f rus. гармоническая функция, f pranc. fonction harmonique, f … Fizikos terminų žodynas
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция неск. переменных, непрерывная в нек рой области вместе со своими частными производными 2 го порядка и удовлетворяющая в этой области дифференциальному ур нию Лапласа … Естествознание. Энциклопедический словарь
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — действительная функция заданная в области Dевклидова пространства имеющая в Dнепрерывные частные производные 1 го и 2 го порядков и являющаяся решением Лапласа уравнения где декартовы прямоугольные координаты точки х. Иногда это определение… … Математическая энциклопедия
Гармоническая функция — (от лат. functio осуществление, исполнение, деятельность) роль, значение аккорда в гармонич. системе мажора и минора, вообще в любой гармонической системе. Г. ф. представляет собой проявление ладовой функции (см. Функции ладовые) в… … Музыкальная энциклопедия
Гармоническая функция
СОДЕРЖАНИЕ
Этимология термина «гармонический» [ править ]
Примеры [ править ]
Примеры гармонических функций двух переменных:
Примеры гармонических функций трех переменных приведены в таблице ниже : r 2 = x 2 + y 2 + z 2 <\displaystyle r^<2>=x^<2>+y^<2>+z^<2>> 
Наконец, примеры гармонических функций от n переменных:
Замечания [ править ]
Связь с теорией сложных функций [ править ]
Хотя указанное выше соответствие с голоморфными функциями справедливо только для функций двух действительных переменных, гармонические функции от n переменных по-прежнему обладают рядом свойств, типичных для голоморфных функций. Они (настоящие) аналитические; у них есть принцип максимума и принцип среднего значения; для них справедлива теорема об устранении особенностей, а также теорема Лиувилля по аналогии с соответствующими теоремами теории комплексных функций.
Свойства гармонических функций [ править ]
Некоторые важные свойства гармонических функций можно вывести из уравнения Лапласа.
Теорема регулярности для гармонических функций [ править ]
Принцип максимума [ править ]
Свойство среднего значения [ править ]
И наоборот, все локально интегрируемые функции, удовлетворяющие свойству (объемного) среднего значения, являются как бесконечно дифференцируемыми, так и гармоническими.
Набросок доказательства. Доказательство свойства среднего значения гармонических функций и его обратного следует непосредственно из наблюдения, что неоднородное уравнение для любого 0 Δ w = χ r − χ s <\displaystyle \Delta w=\chi _\;>
допускает простое явное решение w r, s класса C 1,1 с компактным носителем в B (0, r ). Таким образом, если u гармоничен в Ω
так что u есть потому, что m-кратная повторная свертка χ r имеет класс с носителем B (0, mr ). Так как г и т произвольны, у это тоже. Кроме того, C m − 1 ( Ω m r ) <\displaystyle C^C m − 1 <\displaystyle C^C ∞ ( Ω ) <\displaystyle C^<\infty >(\Omega )\;>
Неравенство Гарнака [ править ]
sup V u ≤ C inf V u <\displaystyle \sup _
Устранение особенностей [ править ]
тогда f продолжается до гармонической функции на Ω (сравните теорему Римана для функций комплексного переменного).
Теорема Лиувилля [ править ]
(Сравните теорему Лиувилля для функций комплексного переменного ).
Эдвард Нельсон дал особенно короткое доказательство этой теоремы для случая ограниченных функций [2], используя свойство среднего значения, упомянутое выше:
Учитывая две точки, выберите два шара с указанными точками в качестве центров и одинакового радиуса. Если радиус достаточно велик, два шара будут совпадать, за исключением сколь угодно малой части их объема. Поскольку f ограничено, его средние по двум шарам произвольно близки, и поэтому f принимает одинаковое значение в любых двух точках.
По свойству усреднения и монотонности интеграла имеем
Обобщения [ править ]
Слабо гармоническая функция [ править ]
Функция (или, в более общем смысле, распределение ) является слабо гармонической, если она удовлетворяет уравнению Лапласа
J ( u ) := ∫ Ω | ∇ u | 2 d x <\displaystyle J(u):=\int _<\Omega >|\nabla u|^<2>\,dx>
Гармонические функции на многообразиях [ править ]
Гармонические функции могут быть определены на произвольном римановом многообразии с помощью оператора Лапласа – Бельтрами Δ. В этом контексте функция называется гармонической, если
Многие свойства гармонических функций на областях в евклидовом пространстве переносятся на эту более общую установку, включая теорему о среднем значении (по геодезическим шарам), принцип максимума и неравенство Гарнака. За исключением теоремы о среднем значении, это простые следствия соответствующих результатов для общих линейных эллиптических уравнений в частных производных второго порядка.
Субгармонические функции [ править ]
Гармонические формы [ править ]
Гармонические отображения между многообразиями [ править ]
D [ u ] = 1 2 ∫ M ‖ d u ‖ 2 d Vol <\displaystyle D[u]=<\frac <1><2>>\int _
СОДЕРЖАНИЕ
Этимология термина «гармонический»
Примеры
Примеры гармонических функций двух переменных:
Наконец, примеры гармонических функций от n переменных:
Замечания
Связь с теорией сложных функций
Хотя указанное выше соответствие с голоморфными функциями справедливо только для функций двух действительных переменных, гармонические функции от n переменных по-прежнему обладают рядом свойств, типичных для голоморфных функций. Они (настоящие) аналитические; у них есть принцип максимума и принцип среднего значения; для них справедлива теорема об устранении особенностей, а также теорема Лиувилля по аналогии с соответствующими теоремами теории комплексных функций.
Свойства гармонических функций
Некоторые важные свойства гармонических функций можно вывести из уравнения Лапласа.
Теорема регулярности для гармонических функций
Принцип максимума
Свойство среднего значения
И наоборот, все локально интегрируемые функции, удовлетворяющие свойству (объемного) среднего значения, являются как бесконечно дифференцируемыми, так и гармоническими.
допускает простое явное решение w r, s класса C 1,1 с компактным носителем в B (0, r ). Таким образом, если u гармоничен в Ω
Неравенство Гарнака
Устранение особенностей
тогда f продолжается до гармонической функции на Ω (сравните теорему Римана для функций комплексного переменного).
Теорема Лиувилля
Эдвард Нельсон дал особенно краткое доказательство этой теоремы для случая ограниченных функций, используя свойство среднего значения, упомянутое выше:
Учитывая две точки, выберите два шара с указанными точками в качестве центров и одинакового радиуса. Если радиус достаточно велик, два шара будут совпадать, за исключением сколь угодно малой части их объема. Поскольку f ограничено, его средние по двум шарам произвольно близки, и поэтому f принимает одинаковое значение в любых двух точках.
По свойству усреднения и монотонности интеграла имеем
Обобщения
Слабо гармоническая функция
Функция (или, в более общем смысле, распределение ) является слабо гармонической, если она удовлетворяет уравнению Лапласа
Гармонические функции на многообразиях
Гармонические функции могут быть определены на произвольном римановом многообразии с помощью оператора Лапласа – Бельтрами Δ. В этом контексте функция называется гармонической, если
Многие свойства гармонических функций на областях в евклидовом пространстве переносятся на эту более общую установку, включая теорему о среднем значении (по геодезическим шарам), принцип максимума и неравенство Гарнака. За исключением теоремы о среднем значении, это простые следствия соответствующих результатов для общих линейных эллиптических уравнений в частных производных второго порядка.