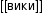Что такое гамма в криптографии
Гаммирование
Гамми́рование — симметричный метод шифрования, основанный на «наложении» гамма-последовательности на открытый текст. Обычно это суммирование в каком-либо конечном поле, например в поле GF(2) такое суммирование принимает вид обычного «исключающего ИЛИ».
Содержание
Визуальное представление
Стойкость
Шеннон доказал, что при определённых свойствах гаммы этот метод шифрования является абсолютно стойким.
Пусть, X и Y случайные величины дискретного типа. X — случайная величина для открытого текста, Y — случайная величина для гаммы, тогда закон распределения X будет выглядеть так:
Используем p и 1-p, так как вероятность встречаемости букв в разных словах различна. Закон распределения Y:
То есть в качестве гаммы подаётся одинакового количество единиц и нулей (у Y симметричный закон распределения). Z — случайная величина дискретного типа для закрытого текста. Из картинки выше видно, что Z=X+Y(mod 2). Вычислим вероятности встречаемости нулей и единиц в законе распределения Z:
1. P(A+B)=P(A)+P(B), если A и B не совместны.
2. P(A*B)=P(A)*P(B), если A и B независимы.
p*1/2+(1-p)*1/2 = 1/2 (для любого p!)
То есть закон распределения Z:
Таким образом, закон распределения Z оказывается симметричным, то есть получается та же гамма или шум (Z не содержит никакую информацию из X, то есть в Z нет p). Это доказывает что шифр является абсолютно стойким.
Требования к гамме
Литература
1. В. В. Ященко — Введение в Криптографию
Ссылки
См. также
Полезное
Смотреть что такое «Гаммирование» в других словарях:
Гаммирование — преобразование исходного (открытого) текста, при котором символы исходного текста складываются (по модулю, равному мощности алфавита) с символами псевдослучайной последовательности, вырабатываемой по определенному правилу. См. также: Гаммирование … Финансовый словарь
гаммирование — кодирование Словарь русских синонимов. гаммирование сущ., кол во синонимов: 1 • кодирование (12) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
гаммирование — Процесс наложения по определенному закону гаммы шифра на открытые данные для их зашифровывания. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом EN gamming … Справочник технического переводчика
Гаммирование — 1. Процесс наложения по определенному закону гаммы шифра на открытые данные Употребляется в документе: ГОСТ 28147 89 … Телекоммуникационный словарь
ГОСТ 28147-89 — Создатель: КГБ, 8 е управление Создан: 1989 г. Опубликован … Википедия
ГОСТ 28147—89 — Создатель: КГБ, 8 е управление Создан: 1989 г. Опубликован: 1990 г. Размер ключа: 256 бит Размер блока: 64 бит Число раундов: 3216 Тип … Википедия
— ГОСТ 28147 89 Создатель: КГБ, 8 е управление Создан: 1989 г. Опубликован: 1990 г. Размер ключа: 256 бит Размер блока: 64 бит Число раундов: 3216 Тип … Википедия
Kaztoken — Kaztoken персональное средство аутентификации и генерации ЭЦП (электронно цифровой подписи). Устройство производится компанией Цифровой Поток[1]. Содержание 1 Технические характеристики 1.1 … Википедия
кодирование — шифрование, программирование, зашифровывание, гаммирование, шифровка, закодирование, зашифровка, кодировка, зашифрование, гипнотизирование Словарь русских синонимов. кодирование сущ., кол во синонимов: 12 • гаммирование (1) … Словарь синонимов
Гамма — в криптографии псевдослучайная числовая последовательность, вырабатываемая по определенному алгоритму и используемая для зашифрования открытых данных и расшифрования зашифрованных данных. По английски: Gamma См. также: Гаммирование Финансовый… … Финансовый словарь
Простейшие методы шифрования с закрытым ключом
Методы гаммирования
Еще одним частным случаем многоалфавитной подстановки является гаммирование. В этом способе шифрование выполняется путем сложения символов исходного текста и ключа по модулю, равному числу букв в алфавите. Если в исходном алфавите, например, 33 символа, то сложение производится по модулю 33. Такой процесс сложения исходного текста и ключа называется в криптографии наложением гаммы.
Сложим по модулю два двоичные числа 1110 и 1100 :
Каким же образом выполняется расшифрование? Зашифрованное число 2 представляется в двоичном виде и снова производится сложение по модулю 2 с ключом:
Таким образом, при гаммировании по модулю 2 нужно использовать одну и ту же операцию как для зашифрования, так и для расшифрования. Это позволяет использовать один и тот же алгоритм, а соответственно и одну и ту же программу при программной реализации, как для шифрования, так и для расшифрования.
Операция сложения по модулю два очень быстро выполняется на компьютере (в отличие от многих других арифметических операций), поэтому наложение гаммы даже на очень большой открытый текст выполняется практически мгновенно.
Благодаря указанным достоинствам метод гаммирования широко применяется в современных технических системах сам по себе, а также как элемент комбинированных алгоритмов шифрования.
Сформулируем, как производится гаммирование по модулю 2 в общем случае:
На рис. 2.6 показано, как применяется гаммирование к тексту с русскими символами. Символы кодируются в соответствии с принятой кодировкой, а затем производится сложение по модулю 2.
При использовании метода гаммирования ключом является последовательность, с которой производится сложение – гамма. Если гамма короче, чем сообщение, предназначенное для зашифрования, гамма повторяется требуемое число раз. Так в примере на рис. 2.6 длина исходного сообщения равна двенадцати байтам, а длина ключа – пяти байтам. Следовательно, для зашифрования гамма должна быть повторена 2 раза полностью и еще один раз частично.
Гаммирование
Гамми́рование (gamma xoring) — метод шифрования, основанный на «наложении» гамма-последовательности на открытый текст. Обычно это суммирование в каком-либо конечном поле (например, в поле GF(2) такое суммирование принимает вид обычного «исключающего ИЛИ»). При расшифровании операция проводится повторно, в результате получается открытый текст.
Шифрование / дешифрирование данных в режиме гаммирования. Криптосхема алгоритма шифрования в режиме простой замены, записывается заполнение КЗУ и блока подстановок. Сначала равновероятно и взаимосвязано генерируется 64 бита синхропосылки, которая разделяется на начальные левый и правый подблоки длиной по 32 бита:
Подблоки синхропосылки зашифровываются в режиме простой замены в течение 32 циклов шифрования: Образованные в итоге 32-го цикла левый и правый подблоки записываются в накопителе и накопителе, как значения и соответственно. Заполнение накопителя складывается в сумматоре СМ по модулю с 32-битовой криптографической константой. Соответственно заполнение накопителя складывается в сумматоре СМ по модулю с 32-битовой криптографической константой:
С выхода сумматора СМ новое значение запоминается в накопителе. Соответственно, с выхода сумматора СМ новое значение запоминается в накопителе. В течение 32 циклов значения и зашифровываются в режиме простой замены, образуя первый 64-разрядный блок шифрующей гаммы, состоящей из правого и левого полублоков:
Полублоки шифруемой гаммы записываются в регистр последовательно сдвига, из которого побитно считаются для шифрования битов первого 64-разрядного блока открытого сообщения. Очередной бит блока сообщения шифруется в режиме гаммирования путем поразрядного сложения по модулю 2 в сумматоре СМ с очередным битом блока шифрующей гаммы:
Сформированные таким образом 64 бита составляют первый блок криптограммы. Для шифрования второго и последующих блоков открытого сообщения из накопителей и считываются значения и, складываются с соответствующими криптографическими константами и полученные значения запоминаются в указанных накопителях. Далее формирование использование второго и последующих блоков шифрующей гаммы выполняется в соответствии с (4.25) и (4.26). По каналу связи или в память ЭВМ последовательно передаются синхропосылки и сформированные блоки криптограммы. Криптосистема алгоритма при расшифровывании в режиме гаммирования имеет вид, аналогичный криптосистеме шифрования (рис. 4.9). Из полученной синхропосылки, идентично процессу формирования блоков шифрующей гаммы, последовательно формируются блоки дешифрующий гаммы, которые используются для дешифрирования принятых блоков криптограммы по правилу:
Алгоритм шифрования в режиме гаммирования по ГОСТ 28147-89 является реализацией режима обратной связи по выходу блочного шифра и позволяет обеспечить помехоустойчивую шифрованную связь при передаче данных по каналам связи с ошибками, так как размножения ошибок при расшифровании не происходит. Для исключения снижения криптостойкости при повторном использовании одного и того же оперативного ключа необходимо в каждом сеансе связи использовать неповторяющуюся синхропосылку. Алгоритм шифрования в режиме гаммирования при возможности имитовоздействия со стороны нарушителя необходимо использовать совместно с алгоритмом выработки имитоставки.
Шифрование / дешифрирование данных в режиме гаммирования. Криптосхема алгоритма шифрования в режиме простой замены, записывается заполнение КЗУ и блока подстановок. Сначала равновероятно и взаимосвязано генерируется 64 бита синхропосылки, которая разделяется на начальные левый и правый подблоки длиной по 32 бита:
Подблоки синхропосылки зашифровываются в режиме простой замены в течение 32 циклов шифрования:
Образованные в итоге 32-го цикла левый и правый подблоки
записываются в накопителе и накопителе, как значения и соответственно. Заполнение накопителя складывается в сумматоре СМ по модулю с 32-битовой криптографической константой. Соответственно заполнение накопителя складывается в сумматоре СМ по модулю с 32-битовой криптографической константой :
С выхода сумматора СМ новое значение запоминается в накопителе. Соответственно, с выхода сумматора СМ новое значение запоминается в накопителе. В течение 32 циклов значения и зашифровываются в режиме простой замены, образуя первый 64-разрядный блок шифрующей гаммы, состоящей из правого и левого полублоков:
Полублоки шифруемой гаммы записываются в регистр последовательно сдвига, из которого побитно считаются для шифрования битов первого 64-разрядного блока открытого сообщения. Очередной бит блока сообщения шифруется в режиме гаммирования путем поразрядного сложения по модулю 2 в сумматоре СМ с очередным битом блока шифрующей гаммы:
Сформированные таким образом 64 бита составляют первый блок криптограммы. Для шифрования второго и последующих блоков открытого сообщения из накопителей и считываются значения и, складываются с соответствующими криптографическими константами и полученные значения запоминаются в указанных накопителях. Далее формирование использование второго и последующих блоков шифрующей гаммы выполняется в соответствии с (4.25) и (4.26). По каналу связи или в память ЭВМ последовательно передаются синхропосылки и сформированные блоки криптограммы. Криптосистема алгоритма при расшифровывании в режиме гаммирования имеет вид, аналогичный криптосистеме шифрования (рис. 4.9). Из полученной синхропосылки, идентично процессу формирования блоков шифрующей гаммы, последовательно формируются блоки дешифрующий гаммы, которые используются для дешифрирования принятых блоков криптограммы по правилу:
Алгоритм шифрования в режиме гаммирования по ГОСТ 28147-89 является реализацией режима обратной связи по выходу блочного шифра и позволяет обеспечить помехоустойчивую шифрованную связь при передаче данных по каналам связи с ошибками, так как размножения ошибок при расшифровании не происходит. Для исключения снижения криптостойкости при повторном использовании одного и того же оперативного ключа необходимо в каждом сеансе связи использовать неповторяющуюся синхропосылку. Алгоритм шифрования в режиме гаммирования при возможности имитовоздействия со стороны нарушителя необходимо использовать совместно с алгоритмом выработки имитоставки. |thumb]]
Гамма последовательность (gamma sequence) Генерация, абсолютно стойкие системы, длина гаммы.
Криптуем по-крупному. Разбираемся с режимом гаммирования из ГОСТ 34.13—2015
Содержание статьи
В одной из статей, посвященных отечественной криптографии, мы разобрались, как применять блочные криптоалгоритмы «Кузнечик» и «Магма» для шифрования сообщений, размер которых превышает размер одного блока (для «Кузнечика» он составляет 16 байт, а для «Магмы» — 8 байт) с использованием режима простой замены (ECB, от английского Electronic Codebook). Этот режим описан в ГОСТ 34.13—2015 «Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров». Этот нормативный документ, помимо режима простой замены, определяет еще несколько способов применения блочных шифров, а именно:
Что ж, давай разберемся, как работает гаммирование и как его применять на практике.
В настоящее время ГОСТ 34.12—2015 и ГОСТ 34.13—2015 обрели статус межгосударственных (в рамках нескольких государств СНГ) и получили наименования соответственно ГОСТ 34.12—2018 и ГОСТ 34.13—2018. Оба стандарта введены в действие в качестве национальных стандартов Российской Федерации с 1 июня 2019 года.
Общие принципы реализации режима гаммирования
Гамма шифра
Гаммирование — это наложение (или снятие при расшифровке сообщений) на открытое (или зашифрованное) сообщение так называемой криптографической гаммы. Криптографическая гамма — это последовательность элементов данных, которая вырабатывается с помощью определенного алгоритма. Наложение (или снятие) гаммы на блок сообщения в рассматриваемом нами стандарте реализуется с помощью операции побитного сложения по модулю 2 (XOR). То есть при шифровании сообщений каждый блок открытого сообщения ксорится с блоком криптографической гаммы, длина которого должна соответствовать длине блоков открытого сообщения. При этом, если размер блока исходного текста меньше, чем размер блока гаммы, блок гаммы обрезается до размера блока исходного текста (выполняется процедура усечения гаммы).
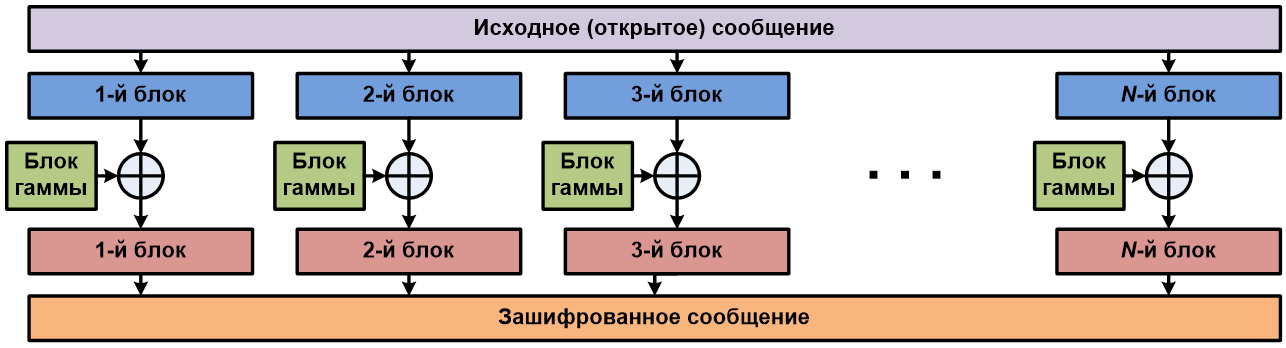
Для дешифровки закрытого сообщения необходимо произвести обратную операцию. То есть каждый блок зашифрованного сообщения ксорится с блоком гаммы, и на выходе мы имеем требуемое расшифрованное сообщение.
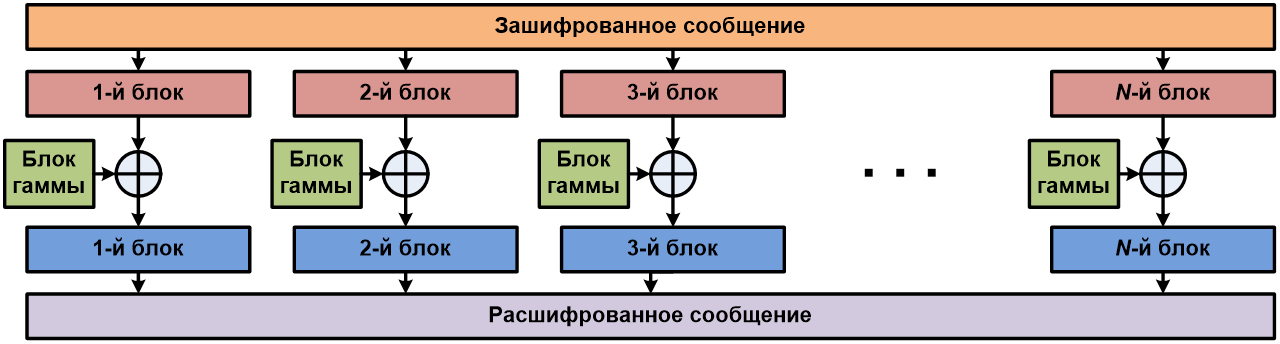
В большинстве случаев размер блока исходного текста принимается равным размеру блока используемого алгоритма блочного шифрования (напомню, это 16 байт при использовании алгоритма «Кузнечик» или 4 байт при использовании «Магмы»), поэтому процедура усечения блока гаммы может понадобиться только для последнего блока исходного текста, в случае, когда общая длина сообщения не кратна размеру одного блока и последний блок получается неполный.
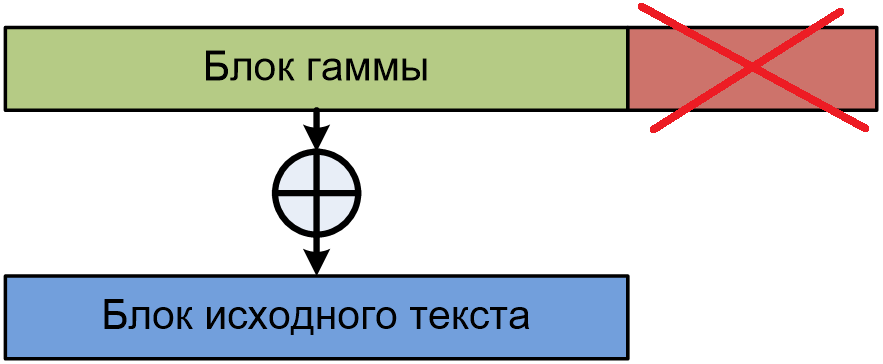
Чтобы обеспечить высокую стойкость шифрования, блоки гаммы должны отличаться друг от друга, а также иметь случайный (или псевдослучайный) характер. В данном случае блоки различаются благодаря так называемому инициализирующему вектору, значение которого меняется от блока к блоку. Псевдослучайность блоков гаммы при этом реализуется путем шифрования этого вектора с использованием выбранного алгоритма (мы используем «Магму»).
Инициализирующий вектор
Значение этого вектора формируется из так называемой синхропосылки, которая представляет собой число определенной длины. Для режима гаммирования длина этого числа должна быть равна половине размера одного блока используемого алгоритма блочного шифрования. Само значение синхропосылки для режима гаммирования должно быть уникальным для каждого цикла шифрования, проведенного с использованием одинаковых ключей, при этом требований к конфиденциальности синхропосылки не предъявляется (то есть ее можно передавать в открытом виде вместе с зашифрованным сообщением).
В режиме гаммирования инициализирующий вектор формируется дополнением нулями синхропосылки до размера одного блока используемого алгоритма блочного шифрования. В случае «Магмы» длина синхропосылки равна четырем байтам, длина инициализирующего вектора — восьми. Вторая часть инициализирующего вектора (заполненная нулями) будет использоваться в качестве того самого счетчика (Counter), который и лег в основу англоязычного сокращения CTR.
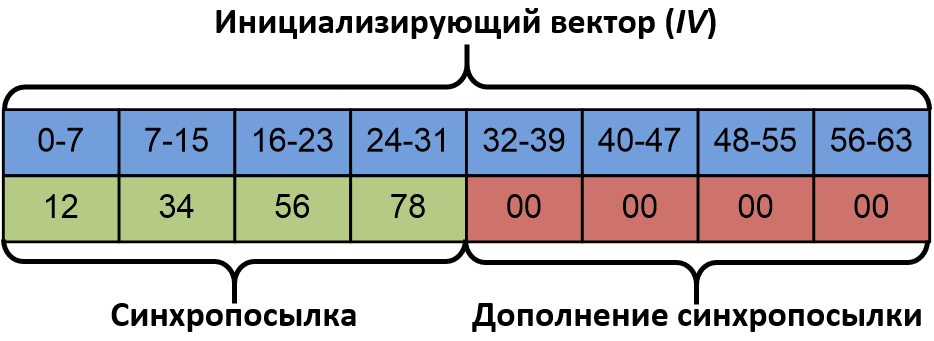
Очередной блок гаммы шифра получается благодаря шифрованию значения счетчика (его начальное значение равно инициализирующему вектору) с помощью выбранного алгоритма блочного шифрования, при этом после выработки очередного блока гаммы значение счетчика увеличивается на единицу.

Продолжение доступно только участникам
Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте
Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее
Шифры замены и табличного гаммирования
В данной работе рассматриваются шифры замены и табличного гаммирования. Читателю предлагается поучаствовать в процессе решения несколько задач из области защиты информации.
Допустим, что устройства читателя подвергаются атаке со стороны неизвестного хакера.
Нарушитель, хакер, злоумышленник не ограничивается выводом из строя устройств. Он их перепрограммирует с целью принудить владельца выполнять какие-то требования либо банального вымогательства у владельца устройств некоторой денежной суммы. Объявляет о требованиях, например, звонком по сотовому телефону и диктует условия (цену) за восстановление работоспособного состояния устройства. Информационная подсистема приборов защищена шифрами разной сложности. Нарушитель использует свои параметры этих разных шифров для затруднения владельцу самостоятельно восстановить работоспособность устройств.
Некоторые положения теории криптологии
Математическая модель произвольного шифра замены SА = (Х, К, Y, E, D), где
X – символ (фрагмент) открытого текста в алфавите А, |A| = n;
Y– символ шифртекста в алфавите В, |B| = m;
K – ключ шифра k =1(1)K; Ek – преобразование зашифрования с ключом kз;
Dk – преобразование расшифрования с ключом kp.
Требования к криптографической системе (КГС)
реализуемость и неизменность шифралгоритма программная и аппаратная;
преобразования, используемые в шифралгоритме должны быть обратимыми;
владение шифралгоритмом не должно способствовать вскрытию ключ;
совпадение объемов (длина шифрованного равна длине исходного) текстов;
любой возможный ключ должен обеспечивать равновероятную защиту;
отсутствие просто устанавливаемых зависимостей между ключами в сеансах связи;
прочтение шифртекста только с соответствующим ключом;
малые изменения ключа должны существенно менять шифртекст прежнего исходного;
малые изменения исходного текста при одном ключе существенно меняют шифртекст;
дополнительные символы к исходному тексту надежно скрываются в шифтексте;
число операций в атаке перебором ключей ограничивается возможностями компьютера;
число операций при атаке на ключ должно быть не меньше числа возможных ключей.
Требования к криптографическим примитивам [8]
биективность (при n=m), регулярность или (n,m,k)-эластичность векторного отображения;
высокая степень корреляционной иммунности;
большая алгебраическая степень и высокая нелинейность;
низкие автокорреляционные показатели, обеспечение строгого лавинного критерия.
Открытый текст прочитывается в первой строке, затем последний символ второй строки и далее справа налево, не прерываясь, в третьей и четвертой строках. Слова в клетки вписаны без пробелов
Для защиты информационной подсистемы «умного» устройства используется простая криптографической система, использующая алфавит естественного языка (русского). В сценарии участвуют два субъекта: владелец устройства и хакер. Владелец знает, что алфавит естественного языка (ЕЯ) предварительно подвергается преобразованию путем умножения на известную ему перестановку 32 степени. Буквы е и ё считаются одной буквой поэтому размерность алфавита не 33, а 32 буквы. Тексты пишутся без пробелов.
Задача читателя, который получил доступ к смешанному алфавиту, состоит в полном восстановлении работоспособности умного устройством (текстов команд), получении возможности замены смешанного алфавита другим (собственным) и зашифровании на его основе текстов (команд управления), которые появляются на экране устройства.
Отметим, что при работе с шифрами учитываются законы естественных языков (ЕЯ):
закон избыточности текстов,
закон частоты встречаемости элементов (букв, слов, n-грамм ) текста,
Простая одноалфавитная замена (без ключа)
Задача №1
Устройство перестало подчиняться командам (отказало), подверглось атаке нарушителя. После простейших проверок наличия внешних дефектов, энергоинтерфейсов, запаха горелой проводки изоляции не чувствуется, а на экранчике дисплея появилось (см. ниже
Зашифрованное сообщение №1
ъ ы п т к ю з г ю я ъ ы п ч к с ы э
Это набор из 18 символов <ъыпткюзгюяъыпчксыэ>, кажущийся бессмысленным. Но на самом деле нарушитель что-то сообщает владельцу на экране и исключает возможность использования устройства по назначению. Попробуем расшифровать оставленное злоумышленником сообщение. Для этого сформируем в таблице 1 перестановку, т.е. последовательность символов (букв) смешанного алфавита (четвертая строка).
Вторая строка частота встречаемости букв (в тысячных долях) естественного алфавита (третья строка), последняя (четвертая строка) содержит переставленные перестановкой Р 32 степени буквы ЕЯ
Шифрование текста нарушителем. В регистр загружается открытый текст и заменяем каждую его букву символом из 4-й строки (табл. 1), этот символ появляется на экране устройства (вторая строка таблицы 2)
При расшифровании символы верхней строки вписываются по мере их раскрытия, а вторая строка заполняется, считывается с экрана, взломанного устройства
Расшифрование текста с экрана. С каждым символом хакерского шифртекста экрана последовательно входим в таблицу 1 (нижняя строка) и в третьей ее строке находим соответствующий символ исходного (не шифрованного, открытого) текста хакера. Пройдя все 18 символов удается восстановить текст от хакера, его пожелание владельцу устройства «прочитайте про шифры».
Одноалфавитная замена с ключом
Задача №2
Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не только смешанный алфавит, но вводится новый элемент в алгоритм шифрования, называемый ключом.
Определение. Ключом называется секретная последовательность символов алфавита (слово) фиксированной длины, возможно осмысленная, что совсем не обязательно, используемая при преобразовании открытого текста в шифрованный и обратно.
Таким образом, к характеристикам ключа относятся:
доступность – закрытый, открытый (в двухключевых шифрах),
алфавит – языка страны,
длина – число букв (символов),
состав – названия всех букв ключа,
порядок – следование букв состава ключа (осмысленный или нет),
срок – длительность использования.
Введение в алгоритм шифрования нового элемента «ключа» способствует при замене символа «х» открытого текста символом «у» шифрованного текста при очередном повторном появлении символа «х» заменить его не символом «у», как первый раз, а каким-то другим, на который укажет символ ключа. Подсчет нарушителем встречаемости символов открытого и шифрованного текста, не позволяет ему правильно сопоставлять пары таких символов, так как частота символов шифртекста стала отличной от прежней. Действительно, одному символу открытого текста стали соответствовать несколько разных символов шифртекста. Наглядно это увидим на конкретном примере.
Пусть, как и раньше, на экране устройства хакер написал свой текст (он изменился):
Зашифрованное сообщение №2
ю я и ю ю я и ю ю я и ю ю я и ю ю я
Этот текст возник иначе, чем в задаче 1, т.е. другим путем (с использованием ключа) отличным от способа шифрования в задаче 1. В качестве ключа используется короткое 4-х буквенное слово «ТЕСТ».
Шифрование. В таблице 3 верхняя строка заполнена открытым текстом хакера, а под ней выписан многократно без пробелов ключ ТЕСТ. В третью строку вписываются символы шифрованного текста, взятые из последней строки таблицы 1
Заливкой выделены повторяющиеся группы из 4-х символов, что может указывать на длину ключа
Задача №3
Шифрование. Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не только смешанный алфавит, но вводится новый элемент в алгоритм шифрования, называемый ключом. Как влияет длина ключа на шифртекст? Изменим (увеличим на 1 символ) длину ключа. В таблице 4 верхняя строка заполнена открытым текстом хакера, а под ней выписан многократно без пробелов ключ ТЕКСТ. В третью строку вписываются символы смешанного алфавита, взятые из последней строки таблицы 1
Пусть, как и раньше, на экране устройства хакер (нарушитель) написал свой текст:
Зашифрованное сообщение №3 (текст опять изменился)
ю я л и ю ю я л и и ю ю я л и ю ю я л
Получилась очень похожая на предыдущую картинка, просто повторов стало меньше, а длина ключа возросла на 1 символ.
Многоалфавитная замена с ключом, гаммирование
Рассмотрение проблемы с атакой на шифры, которая использует частотные зависимости ЕЯ, привело к мысли использовать в алгоритме шифрования не только ключ, что как мы видели в задачах 2,3 оказалось не очень удачным решением (легко определяется длина ключа, повторяющиеся символы), но и более чем один (множество) смешанных алфавитов.
Ниже мы подробно рассмотрим схему шифрования с этими нововведениями и некоторые факторы, влияющие на стойкость шифра к атакам
Задача №4
В этой задаче используется множество смешанных алфавитов, организованных в квадрат Виженера, а ключи используются прежние.
Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не единственный смешанный алфавит, а их множество с применением циклического сдвига каждого последующего на один символ относительно предыдущего. Вытолкнутый циклическим сдвигом символ из начала алфавита помещается в конец списка букв алфавита так, что полная длина алфавите не меняется.
При одноалфавитной замене без ключа всегда символ «х» (буква) исходного (открытого) текста заменялась одной и той же буквой «у» смешанного алфавита, и частота использования х и у была одинаковой, совпадающей с частотой встречаемости символа «х» в ЕЯ. При многоалфавитной замене нарушитель понимает, что символ «х» при каждом очередном появлении в открытом тексте заменяется разными буквами из разных смешанных алфавитов. Этот факт не дает возможности нарушителю напрямую воспользоваться частотным законом ЕЯ, так как частота встречаемости символов открытого текста осталась прежней, но частота встречаемости символов шифрованного текста стала совершенно другой.
Зашифрованное сообщение №4 (текст опять изменился)
у и р г а т н э ь л з ш з ц ч ж ш з
Что же такое нарушитель желает сообщить владельцу «умного» устройства? Стремление разобраться в шифрованном сообщении приводит к необходимости детального анализа ситуации с шифрами и текстами открытыми и шифрованными. Прежде всего, необходимо уяснить как будет использоваться множество смешанных алфавитов, какое их количество задействуется в алгоритме и как эти алфавиты соотносятся друг с другом. Ответ на эти вопросы помогает найти новая таблица 5, названная квадратом 32×32 (таблицей) Виженера. Сколько смешанных алфавитов следует привлекать в алгоритме шифра? Как выбрать ключ шифра?
Строкам таблицы Виженера соответствуют символы (буквы) ключа. Из этого следует, что при шифровании используются столько строк квадрата Виженера, сколько букв содержит ключ шифра (при условии отсутствия повторов). Так как ключом может быть произвольная последовательность букв, то строкам квадрата соответствует полный алфавит. Колонкам квадрата соответствуют символы исходного текста – также полный алфавит.
Таким образом, в этом квадрате размещаются 32 смешанных алфавита (см таблица 1) по горизонтали и по вертикали. Каждый алфавит в этих линиях сдвигается (изменяется) на один символ относительно предыдущей линии, и этот символ вписывается после последнего символа в конце списка. Верхняя строка и вторая колонка – это алфавит ЕЯ с исходным упорядочением букв, т.е. каждая строка и столбец помечены буквой стандартного алфавита.
Из множества возможных перемешиваний алфавита Б. Виженер предложил использовать только n = 32. Способ их получения из первого путем циклического сдвига на каждом шаге на одну позицию.
Процесс шифрования. Исходный текст без пробелов вписывается в линейный регистр. Каждой букве отводится своя ячейка регистра. Ниже этого регистра помещается другой регистр, в который вписывается ключ ТЕСТ шифра. Если ключ шифра короче текста, то ключ вписывается многократно один за другим без пробелов. Таким образом, каждая буква исходного текста соответствует некоторой букве ключа. Это можно отобразить так «хи» → «хk».
Первой букве открытого (столбец) текста соответствует первая буква ключа (строка)
«хи =П»→«хk=т». Переходим в квадрат Виженера. Строка квадрата обозначена буквой «т» ключа, а столбец квадрата определяется буквой открытого текста «П». В клетке пересечения выбранных линий (строки, столбца) находится буква шифртекста «уш = у». Формально эти действия описываются цепочкой «хk = т» → «хи = П» → «уш = у» из трех символов: тПу.
Дальше все повторяется до исчерпания открытого текста. Результатом такого шифрования является третья строчка таблицы 6. Именно она появляется на экране дисплея умного устройства.
Анализ текста с экрана. Из примера для ключа «ТЕСТ» видим, что первая буква ИТ П заменяется на У, которая взята в строке квадрата, помеченной буквой Т ключа, и в колонке квадрата, соответствующей (помеченной) букве П.
Второй раз, когда буква П встречается в ИТ замена (буква 3) для нее берется в строке, ключа, помеченной буквой С (не как раньше буквой т), и в той же самой колонке для буквы П. Уже отсюда видим, что подсчет частот встречаемости буквы П в исходном тексте и символов замены для этой буквы в шифрованном тексте не совпадают, что не позволяет напрямую воспользоваться законом частоты повторяемости букв при вскрытии шифртекста.
Во-первых, в ключе могут быть повторяющиеся буквы и для них используется одна и та же строка квадрата Виженера:
Во-вторых, не исключается возможность совпадений (наложений) одинаковых непрерывных участков ИТ на одинаковые непрерывные участки ключа.
К чему это может привести будет рассмотрено на примере оцифровки для второго более длинного ключа «ТЕКСТ».
Анализ исходного текста и шифртекста с ключом ТЕСТ показывает следующее: в ИТ имеются две повторяющиеся триграммы «ПРО», в скобках за буквами пишем какими буквами они заменились в шифртексте: Р(И, Ш, Ш) встречается три раза; буквы П (У, З), О(Р З), Т(Т, Ь), И(А, Б) – по два раза; Ч(Г), А(Н),Й(Э),Е(Л),Ш(Ц),Ф(Ж),Ы(З).
Наш ограниченного объема пример позволил продемонстрировать все возможности замен. Хотя ключ ТЕСТ содержит четыре буквы, но различных среди них только три. Следовательно, при шифровании будут использованы только три различных смешанных алфавита.
Задача №5
Процесс шифрования. В этой задаче также используется множество смешанных алфавитов, организованных в квадрат Виженера. Используется более длинный ключ ТЕКСТ.
Первой букве открытого текста соответствует первая буква ключа «хи =П»→«хk=т».
Переходим в квадрат Виженера. Строка квадрата обозначена буквой «т» ключа, а столбец квадрата определяется буквой открытого текста «П». В клетке пересечения выбранных строки и столбца находится буква шифртекста «уш = у». Формально эти действия описываются цепочкой «хk = т» → «хи = П» → «ущ = у» из трех символов: тПу.
Дальше все повторяется до исчерпания открытого текста. Результатом такого шифрования является третья строчка таблицы 7. Именно она появляется на экране дисплея умного устройства.
Зашифрованное сообщение №5
у и ч к а ь я о в т у и ч г а ж и я
Будем пытаться прочесть это сообщение в ходе анализа шифртекста.
Анализ и дешифрование текста с экрана. Ключ ТЕКСТ содержит пять букв, из них различных только четыре, и с этим ключом будут использованы четыре различных смешанных алфавита. Какой же из ключей обеспечивает большую устойчивость к взлому (расшифрованию)?
Казалось-бы, тот шифр, который использует большее число различных алфавитов, что приводит к замене одной и той же буквы ИТ большим числом других букв, и лучше ее маскирует. Но, увы, это не общее правило. Наш пример призван это подтвердить.
Все ситуации замены при шифровании могут быть описаны следующим перечнем:
одинаковые буквы ИТ (П(УУ), Р(ИИИ), О(ЧЧ), И(АА),) заменяются одинаковыми в ШТ (У, И, Ч, А);
одинаковые буквы ИТ (Т) заменяются разными в ШТ (Ь, В);
разные буквы ИТ(Ч, А, Й, Е, Ш, Ф, Ы) заменяются разными в ШТ(К, Я, О, Т, Г, Ж, Я);
разные буквы ИТ (А, Ы) заменяются одинаковыми в ШТ (Я).
Определение длины ключа. Причиной появления одной и той же буквы Y в ШТ может быть либо совпадение буквы X в ИТ и буквы ключа под ней; либо на Y была заменена другая буква из ИТ при использовании сдвинутого смешанного алфавита.
Действительно, в исходном тексте буква Р попадает трижды на букву Е ключа ТЕКСТ во 2-й, 12-й и 17-й позициях и заменяется буквой И из одного и того же смешанного циклически сдвинутого алфавита. Этот алфавит в квадрате Виженера соответствует строке, помеченной буквой Е ключа. Интервалы между повторениями буквы И кратны числу 5. Все три интервала кратны 5.
17 – 12 = 5, 17 – 2 = 15, 12 – 2 = 10.
Аналогично с буквой У в 1 и 11— й позициях ШТ, интервал 11 – 1=10 кратен 5; с буквой Ч в 3-й и в 13-й позициях ШТ; интервал равен 13 – 3 = 10, что также кратно 5. Буква Я в позициях 7-й и 18-й ШТ не удовлетворяет общему правилу 18 – 7=11, что не кратно 5, а вот буква А в ШТ в позициях 5-й и 15-й опять подчинена правилу, интервал 15 – 5 = 10 кратен 5.
Как только решен этот вопрос сразу же становится возможным определение списков букв ШТ, которые были зашифрованы одним и тем же смешанным алфавитом. Не зная самого ключа, мы должны полагать, что используются пять различных алфавитов (по числу букв в ключе), т.е. пять строк квадрата Виженера.
Множество всех букв ШТ теперь можно расчленить на L = 5 групп, таким образом, что в каждой группе соберутся буквы из одной строки квадрата Виженера, т. е. из одного смешанного алфавита. Таким образом удается свести задачу к нескольким последовательным, но одноалфавитной замены для каждого. А это уже задача из числа успешно решаемых. Как же осуществить разбиение букв?
На этом этапе вскрытия шифрограммы перед нами встает задача выбора дальнейшего пути исследования. Если бы выборки в каждой группе были значительными (более 700 букв), то используя закон частоты встречаемости буквы, сопоставив частоту появления букв в русском языке и в каждой группе, а также учитывая семантику вскрываемого текста можно было бы и завершить решение задачи, но при малых выборках ожидать успеха на этом пути не приходится.
Можно ли каким-то образом получить такие матрицы, не располагая данными о ключе?
Эта информация может явиться той основой, которая позволит выявить сам ключ, т.е. слово. Ясно, что, зная величину сдвигов между алфавитами, можно пытаться подобрать слово из букв стандартного алфавита по маске, которая учитывает структуру самих сдвигов. Поиск может выполняться с использованием словарей или с визуальным контролем. Надо полагать, что ключ будет осмысленным словом или даже фразой. Это и должно использоваться при контроле в процессе поиска ключа.
Покажем на нашем примере как такой поиск выполняется. Построим (гребенку (Рис. 1 которая будет играть роль движка или шаблона (маски). Разность между крайними отметками на гребенке равна модулю наибольшего сдвига между алфавитами. Отметим крайние положения (зубцы) гребенки номерами наиболее раздвинутых алфавитов (в примере наиболее удаленных друг от друга букв Т и Е ключа) как 1 и 2. Все другие положения на гребенке определяются относительными расстояниями (сдвигами) алфавитов, занимающих промежуточное положение между выявленными крайними.
Снабдим их соответствующей нумерацией 3, 4, 5. Теперь, если перемещать движок- гребенку вдоль стандартного алфавита, помещенного на полоске, склеенной в кольцо, и считывать буквы напротив зубцов, то оказывается, что различных положений у такого движка всего 32 по числу букв в алфавите. Соответственно и буквенных наборов, потенциально образующих ключ такое же число. Остается выяснить путем перебора какая совокупность букв с точки зрения семантики наиболее подходит в качестве ключа. Считаем, что лента с алфавитом склеена в кольцо и движок перемещается по окружности.
На самом деле вопрос о построении гребенки не так прост. В нашем примере мы знаем ключ и соответственно ему нумеровали рабочие алфавиты из квадрата Виженера. При неизвестном ключе мы можем построить гребенку, но нумерация зубцов остается невыясненной. Порядок букв в ключе (относительный) будет определен так. В примере мы крайний правый зубец гребенки снабдили номером 1, а крайний левый номером 2, что соответствует буквам Т и Е стандартного алфавита. Но, не зная ключа, можно было поместить зубцы и наоборот (зубцы на Рис.1 для второй возможности представлены в виде (“-^-“)
Беглый анализ этих совокупностей после прочтения показывает, что совсем непросто получить осмысленный текст при произвольном выборе гребенки. Даже похожих на осмысленные слова совокупностей практически нет. Первая совокупность могла бы быть подозрительной на ключ с учетом того, что допущена ошибка в длине ключа и ключом является слово НАЕМНИК.
Но среди всей этой абракадабры имеется одно единственное вполне осмысленное слово ТЕКСТ (выделено заливкой) и, конечно, только оно может быть принято в качестве ключа.
Заключение
Материал приведенный в публикации знакомит с простыми шифрами алфавитной замены, которые известны с прошлого столетия или еще раньше, но для тех читателей, которые раньше не были знакомы с проблемами информационной безопасности, текст может быть интересен.
Подробно рассмотрено влияние ключа (его длины и состава) на шифртекст. Упоминание о законах естественного языка, которые всегда учитываются в науке криптология может заинтересовать читателей по разным причинам. Так, например, совсем слабо освещена в науке проблема избыточности ЕЯ. Как от нее избавляться или как ее использовать, где эта избыточность размещается в текстах мало что известно.
Архиваторы, сжимающие тексты, существуют давно, но их теория на сформулированные вопросы не отвечает. Более того, часто архиваторы проектируются так, чтобы тексты восстанавливались без потерь, т.е. исходная избыточность текстов восстанавливается.