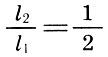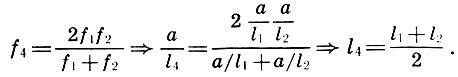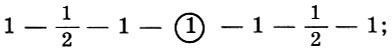Что такое гамма на пианино

Играем гаммы на пианино

Каким бы скучным ни было занятие – проигрывание гамм, без этого – никуда. Гаммы – это развитие моторики и беглости пальцев, постановка руки, выработка идеального звука и нужного звуковедения. А если вы играете гаммы на пианино двумя руками, то развиваете синхронность, внимание и координацию.

Чтобы на данном этапе не загружать вас лишней информацией, поиграем только одну гамму – до мажор. На одном из прошлых уроков я объясняла вам, что такое тональность до мажор. Кто подзабыл или не читал тот урок, напомню: до мажорная гамма – это звукоряд с тоникой ДО. А гамма – это не что иное, как звукоряд в тональности. До мажор – самая любимая тональность у всех начинающих. Почему? Потому что играется она только на белых клавишах.

Начать можно с любой руки. Поиграйте по одной – сначала левой, потом правой. Или наоборот. Кстати, если вы забыли нумерацию пальцев (правильно – аппликатуру), то можете вернуться в тот урок, где это объяснялось, но я повторю. Большой палец – первый, указательный – второй, средний – третий, безымянный – четвертый и мизинец – пятый.

Левой рукой играем гамму с пятого пальца, а правой – с первого.

Не нужно сразу пытаться сыграть гамму на пианино двумя руками – это сложно. Поэтому доведите до автоматизма каждую руку, а потом уже соединяйте. Играйте медленно, торопиться не нужно. Кисть руки должна быть слегка приподнятой, закруглённой. Клавиш касаемся кончиком подушечки — тем местом, где выступает верхушка ногтя. Кстати, обучение игре на пианино и длинные ногти – вещи несовместимые, увы.

Так играют гаммы левой рукой:

А так — правой:

Когда вы освоите гамму до мажор, мы с вами перейдем на арпеджио. Новое слово и новое понятие. Тоже очень полезная штука. Только об этом я расскажу в следующий раз.

Кстати, гаммы на пианино могут звучать очень красиво и привлекательно:

Источник

«Занимательные гаммы» некоторые важные моменты в игре гамм

Разделы: Музыка

В моей педагогической практике часто встречаются дети с небольшими музыкальными способностями и возможностями. Развивать и направлять их помогает мне ряд упражнений, применяемых мною (опираясь на опыт лучших педагогов и их рекомендации) в усвоении гамм. Данным опытом хочу поделиться.

И еще важный момент. Необходимо, чтобы ученик осознавал, что в зависимости от характера звучат различные и пианистические движения, что качество звука связано с соответствующим движением корпуса, руки, палацев. У ученика постепенно должна выработаться автоматическая связь между желаемым звучанием и пианистическим движением, то есть сформироваться так называемое мышечное чувство. Добиваясь необходимого звукового результата, ученик будет совершенствовать свои пианистические движения, физически приспосабливаясь к выполнению постоянной цели. Поэтому, играя гаммы, мы должны стоять перед учащимся конкретные звуковые задачи, учить гаммы различными способами, направляя слуховое внимание на звуковой результат.

Звуковые задачи при игре гамм

2. Играть гаммы с различной артикуляцией (различными штрихами).

3. Развивая методическую точность, играть гаммы с акцентами и в разных ритмах.

4. Играть гаммы с различной нюансировкой, тембровыми и динамическими красками.

5. Во время игры гамм можно развивать полифонический и ансамблевый слух.

Начальный период игры гамм

В начальный период обучения закладывается фундамент пианистической техники, происходит привитие и закрепление навыков. Вот почему так важно их качество. И поэтому сразу нужно прививать только целесообразные движения, не допускать неверных и лишних. Необходимо постоянно следить за свободой пианистического аппарата, предупреждать всякого рода зажатости и скованности.

Художественной задачей этого периода является игра гамм ритмически и динамически ровным, глубоким и мягким звуком. Учиться слышать в гамме мелодическую линию, добиваться линеарности звучания, текучести, чтобы не было ощущения «точечности» звучания. Играть певучим, выразительным legato. При этом вслушиваться в каждый звук и доводить его слухом до конца длительности.

Техническое освоение гамм

По формуле мажора (чередование тонов и полутонов) строим мажорную гамму. Удобнее начинать изучение мажорной гаммы с Си мажора для правой руки и Ре бемоль мажора для левой руки, так как в их звукоряде есть так называемая Формула Шопена. Эту формулу Шопена Г.Нейгауз называл «гениальной по своей дальнобойности» фортепианной формулой. Играя эти гаммы, ученик сразу учиться придерживаться середины клавиатуры, а не спускаться к краям клавиш. Располагая длинные пальцы на четырех клавишах, кисть приобретает естественную, непринужденную форму, исключающую зажим мышц.

Разбиваем данные гаммы на аппликатурные позиции. Первый палец «сохраняет» верность белым клавишам. Остальные пальцы располагаются на черных клавишах.

Для закрепления аппликатурных позиций и удобных мышечных ощущений играем эти позиции интервалами и кластерами.

Ровность при игре гамм зависит от legato внутри позиции и подкладывания первого пальца. Часто при игре гамм приходится сталкиваться с так называемой тряской. Чтобы этого избежать, усвоения приема legato у моих учеников проходит постепенно, начиная с двух нот с дальнейшим добавлением. Так доходим до пяти пальцевой позиции. Основные технические требования к игре legato предъявляются следующие: погружение веса всей руки от плеча через палец в клавишу (контакт с клавиатурой). Нажим пальца в клавишу происходит без толчка, следует плавное переступание с палаца на палец (передача веса). Кисть движется за звуком. При этом необходимо следить, чтобы неиграющие пальцы не напрягались, не оттопыривались, а двигались за играющими. Кисть должна быть все время собранной. Таким образом, кисть и предплечье при игре звуков одной гаммовой позиции делают как бы вспомогательное объединяющее движение.

Кистевые вспомогательные движения

при котором производится «рессорный», упругий нажим, приводящий к некоторой временной фиксации в запястном суставе. Руки движутся друг от друга в разные стороны.

Тренировка гибкости и подвижности первого пальца

Большое значение при игре гамм имеет подкладывание первого пальца и перекладывания через него других пальцев кисти. Первый палец должен быть легким, гибким, подвижным и самостоятельным. Помещать его нужно на край белой клавиши утлом «подушечки» и следить, чтобы не было прогиба первого сустава (закруглен под ладонь). Первый палец должен быть как «опорная свая» всего кистевого «купола», как «ножка циркуля». При таком положении первого пальца кисть не будет терять своей куполообразной формы, и запястье чрезмерно не прогнется вниз.

Для тренировки первого пальца и приобретения им требуемых качеств можно использовать следующие упражнения (см. приложение)

При игре гамм надо следить и сразу предупреждать следующие недостатки учащихся:

1. Пальцы не должны «вязнуть» в клавишах. Взятие и снятие пальцем клавиши должно быть активным и точным. Для этого кончики пальцев нужно слегка фиксировать и нацеливать на взятие клавиш, но высоко их не поднимать.

2. Не прогибать последние фаланги пальцев. Это тоже зависит от фиксации кончиков. Надо зацепить и закрепить кончик пальца на клавише.

3. Не прогибать запястные косточки, ощущать в них опору паяцев, иначе сила от плеча не дойдет до их кончиков.

4. Не «выколачивать» первым пальцем при смене позиций, вслушиваться в ровность звучания гаммы, чтобы не была нарушена звуковая линия.

Осваивать гаммы двумя руками удобно начинать с Ми мажора. Большое количество черных клавиш роднят ее с позицией Шопена. (приложение 24) Остается то же расположение руки на средней линии клавиатуры и ощущение того же мышечного удобства. Ученик знакомится с симметричной,»зеркальной» аппликатурой, запоминая положение 4 пальца: на VII ступени в правой руке и на II ступени в левой.

Для закрепления видов минора и умения свободно переходить из одного в другой, играем по совету Корыхаловой Н. следующее упражнения (приложение 25).

В этот период продолжается закрепление игровых навыков, идет поиск ощущения удобства в игре, отрабатывается пластика пианистических движений. В это время я ставлю перед учеником уже больше художественных задач: динамические и артикуляционные, а также задачи на координацию движений обеих рук в различных динамических и артикуляционных соотношениях. Играя и выполняя данные задачи, учащиеся, учатся связывать качество звука с определенными пианистическими движением: продолжает закрепляться звуко-двигательная связь.

ХУДОЖЕСТВЕННЫЕ ЗАДАЧИ В ИГРЕ ГАММ

1 Сыграть гамму форте (f)

Но кроме объяснения технической стороны извлечения звука f, педагог должен обратиться к музыкально-слуховым представлениям учащихся. Ведь не двигательно-моторный фактор стоит на первом месте в исполнении музыки, а прежде всего мысленное представление звукового образа, осознание художественной цели. А уже слуховые представления помогают ученику найти необходимое пианистическое движение для воплощения на инструменте своего звукового «прообраза». Поиски звука нужного количества и характера приведут учащегося к нахождению целесообразного приема, удобного ощущения. «Что» определяет «как» (Цит. по: 7). У него постепенно будет закрепляться между слуховыми представлениями и необходимыми движениями.

Играя гамму f, маленький ученик будет представлять, как «шагает большой, грузный слон», но «надев мягкие тапочки». Звук получится сильным, но не грубым, глубоким, но не резким, а мягким, благородным. Особенно это будет слышно в низком регистре, в начале движения гаммы.

2. Сыграть гамму пиано (р)

Играя гамму piano, Важно не «шептать», не «прятаться». Звук должен быть опертый, пронизывающий. По выражению Перельмана Н. «пиано должно быть слышно и в сотом ряду зала» (Цит. по: 9). Чтобы добиться нужного качества звука ученику подсказывается пианистический прием: мышцы верхней части руки удерживают ее в подвешенном состоянии, рука легкая, воздушная. Вся нагрузка приходится на пальцы. Возрастает роль цепких, активных, точных, собранных пальцев с упругими, покалывающими клавиши кончиками. Играем легко, прозрачно, с точным «прицелом» пальцев.

Ученики представляют образ «росинок на цветах на утреней заре». Тихое звучание соответствует образу

3. Совершать волнообразное движение

В гамме необходимо слышать постепенное усиление и ослабление звучания. Савинский С. писал, что «над сгеscendo и diminuendo надо работать, как над технически трудными пассажами» (Цит. по: 11).

Ученик должен научится четко соотносить свои физические ощущения (разумное регулирование веса руки с чувством мышечной свободы) со слышимым звуковым результатом. Осознав поставленную звуковую задачу, ученик может сам найти технический прием, который приведет к нужному качеству и характеру звука. Но сначала педагог подсказывает ученику нужное движение, настраивает его слуховую фантазию и определенный образ.

Играем гамму «звуковысотной динамикой»: вверх, сгеscendo вниз diminuendo. Ученики сами придумывают и настраиваются на образ: мы забираемся на гору. При походе к вершине идти становится труднее, мы затрачиваем большие силы и энергии, что ведет к большому напряжению и нажиму руки на клавиатуру, к более глубокому погружению пальцев в клавиши.

Можно представить, как мы приближаемся к. какому-то источнику звука: оркестр, играющий в глубине парка, патефон со старой пластинкой в дальней комнате дома. И по мере приближения к ним звучание становится громче и наоборот. Рука придерживается мышцами плеча, прикосновение пальцев к клавиатуре облегчается.

1. Сыграть гамму кистевым staccato

Играя гамму кистевым staccato в верхнем регистре, делаем плавный, легкий отскок кисти, как бы рисуя образ: «от порыва ветра разлезается одуванчик», «впорхнул мотылек», «росинки блестят на солнце». Тембр звучания «светлый», «мягкий», «прозрачный». Но кончики пальцев должны быть фиксированными, так как легкость звука («росинки маленькие») должна сочетаться с прикосновением пальца до дна клавиши («блеск их на утреннем солнце»)

2. Сыграть гамму пальцевым staccato

Из многочисленных видов приемов игры staccato маленький ученик, прежде всего, должен научится игре кистевым и пальцевым staccato.

3. Сыграть гамму певучим, кантиленным lе gato

В этой фразе слышится настроение звучности к кульминации «ре». Все звуки до опорного «ре» надо объединить одним движением запястья, при этом несколько фиксировано. Рука перемещается плавно, погружается с каждым звуком все глубже и глубже в клавиши. Пальцы находятся с предварительным контактом с клавишами. Нажимом передаем вес руки от плеча через кончики пальцев в дно клавиши и чувствуем эту опору до перехода в следующий звук.

После кульминации звучность спадает. Это сопровождается расслаблением кисти на четырех последних зевках и небольшим «вздохом» кисти на «фа-диез». Кистъ делает гибкое овальное движение перед последним звуком. Пальцы не изолированы, а связаны со всей рукой гибкой и пластичной. Подтекстовка поможет проинтонировать фразу, сыграть более выразительно.

Ритмическая игра гамм будет заключаться в следующем:

1. Игра с акцентами с разной пульсацией (меняется ритмическая группа в одной доле, и начало каждой группы акцентируется).

2. Игра в разных ритмах и в сочетании с различной артикуляцией.

Акценты берутся все время различными пальцами, что развивает их активность и координацию движений. Акцент делается не рукой, а только пальцем. Напряжение пальца на акценте моментально сменяется расслаблением. Здесь нужна активная работа сознания, Дающие четкие «приказы» пальцам, и особенно необходима хорошая связь между слухом и движением: внимательно следить, чтобы акценты, взятые разными пальцами, звучали одинаково. Полезно сделать подтекстовку

2. Играем триолями на 3 октавы (чтобы закончить на тонике) (см. Приложение 28).

3. Играем квартаолями (см. Приложение 29).

4. Играем секстолями на 3 октавы. Увеличивая количество звуков в ритмической группе, исполняемых легкой рукой после акцента, мы играем в более быстром темпе. Это служит одним из этапов в подготовке к игре в быстром темпе (см. Приложение 30).

5. Играя квартаолями, в самой группе меняется место акцента. Начало затактовое (см. Приложение 31).

Игра в разных ритмах в сочетании с различной артикуляцией

1. При игре триолями, квартолями, секстолями используем различные штрихи (см. Приложение 32-а, б, в).

2. Примеры ритмических и артикуляционных сочетаний (см. Приложение 33).

Координационные задачи и развитие полифонического слуха при игре гамм

Часто у учащихся страдает способность координации движения рук, и они не могут согласовать между собой различные задачи, выполняемые разными руками. Ученику необходимо скоординировать составные части музыкальной ткани. Сохраняя независимость каждого элемента музыкальной фактуры. Приобретение навыков координации движения связаны с развитием мышления (надо ясно представить составляющие линии музыкальной ткани, чтобы музыка не звучала однообразным потоком, в котором утонули и ведущие линии, и мельчайшие детали, элементы музыкальной фактуры), слуха (необходимо слышать фактуру музыки в полном объеме) и техники (наиболее важным является гибкость технического аппарата, пластичное взаимодействие всех его звеньев, иначе руки, что называется, «расходятся», одна рука отстает от другой).

Играя гаммы, мы, таким образом, можем рассматривать партии обеих рук как два голоса, самостоятельно ведущие свои мелодические линии, которые могут не совпадать ритмически, артикуляционно и динамически, и которые нужно провести ясно и выразительно. И это будет уже решением задач развития полифонического слуха и мышления. Чтобы тренировать соответствующие мозговые центры, отвечающие за недостатки координации, мы можем поиграть гаммы в следующих вариантах:

1. Различная динамика

Правая рука играет piano (р). Левая играет forte ( f)

Игра с ведущей правой рукой (f ) уже традиционна. А, по мнению Маргариты Лонг, ведущей при игре должна быть левая рука, ей принадлежит «ритмический приоритет» (у которого левая рука развита меньше правой) (Цит. по: 2)

2. Различная артикуляция

3. Различный метроритм

а) можно поиграть упражнение Корыхаловой н. (см. Приложение 34). Здесь одна рука играет роль «дирежора», она отсчитывает опорные доли и тем самым влияет на ритмическую точность;

6) то же упражнение можно поиграть с несовпадающей артикуляцией в партиях обеих рук (см. Приложение 35).

МУЗЫКАЛЬНЫЕ ЗАДАЧИ В ИГРЕ ГАММ

В БОЛЕЕ СТАРШИЙ ПЕРИОД РАЗВИТИЯ УЧЕНИКА

Источник

Пифагорейское математическое обоснование музыкальной гаммы

Глава из книги Александра Волошинова «Математика и искусство» (Москва: Просвещение, 1992)

Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.

Строго говоря, речь здесь пойдет о пифагоровом строе. Что же такое гамма и строй в музыке?

Гаммой, или звукорядом, называется последовательность звуков (ступеней) некоторой музыкальной системы (лада), расположенных, начиная от основного звука (основного тона), в восходящем или нисходящем порядке. Название «гамма» происходит от греческой буквы Гγ (гамма), которой в средние века обозначали крайний нижний тон звукоряда, а затем и весь звукоряд.

Важнейшей характеристикой музыкального звука является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например струны. Чем больше частота колебаний струны, тем «выше» представляется нам звук.

Каждый отдельно взятый звук не образует музыкальной системы и, если он не слишком громкий, не вызывает у нас особой реакции. Однако уже сочетание двух звуков в иных случаях получается приятным и благозвучным, а в других, наоборот «режет» ухо. Согласованное сочетание двух звуков называется консонансом, несогласованное — диссонансом. Ясно, что консонанс или диссонанс двух тонов определяются высотным расстоянием между этими тонами или интервалом.

Интервалом между двумя тонами назовем порядковый номер ступени верхнего тона относительно нижнего в данном звукоряде, а интервальным коэффициентом I₂₁ двух тонов — отношение частоты колебаний верхнего тона к частоте нижнего * :

(6.1)

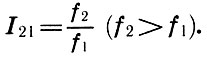
* (В теории музыки понятия интервала и интервального коэффициента строго не разграничены. Следуя традиции, мы часто для краткости будем называть интервальный коэффициент интервалом. )

Рассмотрим теперь некоторую совокупность звуков, нажав, например, на фортепиано последовательно несколько клавиш. Скорее всего, у нас получится бессвязный набор звуков, как говорится, ни складу ни ладу. В других случаях звуки вроде бы подходят, ладятся между собой, но их совокупность покажется оборванной, незаконченной. Эту последовательность так и хочется продолжить до определенной ноты, которая в данной системе звуков кажется наиболее устойчивой, основной и называется тоникой. Итак, звуки в музыкальной системе связаны между собой определенными зависимостями, одни из них являются неустойчивыми и тяготеют к другим — устойчивым.

* (Характер звучания лада, конечно, не определяется столь грубо и однозначно. Вопрос этот очень деликатный, и о нем мы еще поговорим в конце главы. )

Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение. История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха. Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенная) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада — это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю свою жизнь.

Нас же будут в первую очередь интересовать математические закономерности, описывающие строение лада, т. е. музыкальный строй. Музыкальным строем называется математическое выражение определенной системы звуковысотных отношений. Помимо чисто теоретического интереса строй находит применение при настройке музыкальных инструментов с фиксированной высотой звуков, таких, как фортепиано или орган.

В заключение заметим, что наши эксперименты с нажатием клавиш на фортепиано могут закончиться самым редким и самым приятным феноменом, когда взятая система звуков будет не только принадлежать к какому-либо ладу, но и будет носить осмысленный характер. Такой художественно осмысленный последовательный ряд звуков разной высоты называется мелодией. Это как раз то, что мы так любим напевать в зависимости от нашего настроения — бодрого, грустного, веселого…

После такого кратчайшего экскурса в теоретическое музыкознание мы можем вернуться на берега солнечной Эллады во времена мудрого Пифагора. Попытаемся восстановить рассуждения Пифагора и его учеников при построении пифагорова строя, ибо именно этот строй определил на тысячелетия, если не навечно, все развитие музыкальной культуры, не только европейской, но и восточной. Сам Пифагор не оставил никаких письменных работ, да и наследие пифагорейцев представляется безнадежной грудой развалин, т. е. собранием случайно уцелевших фрагментов и более поздних цитат. Бесспорно, развалины эти прекрасны и поныне поражают воображение, как развалины знаменитого Парфенона, однако многое в этих обломках бесследно утеряно и о целом часто можно только догадываться. И все-таки…

Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит. Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.

* (Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )

«Законы Пифагора — Архита», на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:

1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:

(6.2)

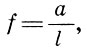
здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).

2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.

Эти интервалы — «совершенные консонансы», и их интервальные коэффициенты позже получили латинские названия * :

* (Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д.)

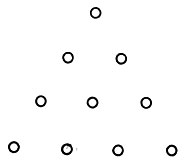
Треугольное число 10

Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида тем созвучнее интервал.

«Второй закон Пифагора — Архита» и сейчас кажется удивительным. Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной.

Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l₁, то вместе со всей струной монохорда длины l₁ = 12l будут созвучны ее части длины l₂ = 6l — звук на октаву выше (l₂/l₁ = l/2), l₃ = 9l — звук на квинту выше (l₃/l₁ = 2/3) и l₄ = 8l — звук на кварту выше (l₄/l₁ = 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это «та гамма, по которой поют сирены». При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.

Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять, т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения. Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f₁ и f₂ = 2f₁, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f₃ = (f₁ + f₂)/2. Но тогда длина струны l₃ выразится через длины струн l₁ и l₂ согласно (6.2) следующим образом:

т. е. l₃ есть среднее гармоническое l₁ и l₂ (см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f₁ и f₂ переходит в среднее арифметическое для длин l₁ и l₂:

Вспоминая, что 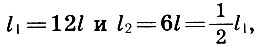мы вместе с Архитом приходим к важному выводу:

(6.3)

(6.4)

т. е. квинта есть среднее гармоническое длин струн основного тона l₁ и октавы l₂, а кварта — среднее арифметическое l₁ и l₂.

Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел:

(6.5)

(6.6)

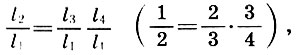
т. е. октава есть произведение квинты на кварту.

(6.7)

которую называли «музыкальной»: октава так относится к квинте, как кварта к основному тону.

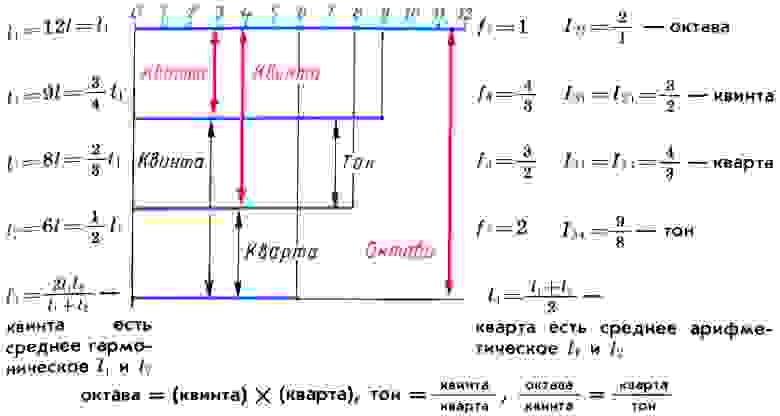
Деление струны монохорда (l₁) на части, образующие с ней совершенные консонансы: октаву (l₂), квинту (l₃) и кварту (l₄) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками

Легко получить еще два соотношения:

(6.8)

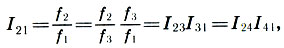
т. е. октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением. Таким образом, квинта есть обращение кварты и наоборот.

Наконец, найдем интервальный коэффициент между струнами квинты l₃ и кварты l₄, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):

(6.9)

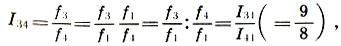
т. е. тон-интервал равен отношению квинты к кварте.

Заметим, что в отличие от обычного расстояния на прямой r₂₁ = х₂ — x₁ определяемого как разность координат конца и начала, интервальный коэффициент — высотное расстояние — определен как отношение составляющих его тонов Тогда три тона f₁ 3 /₂ и среднее гармоническое 4 /₃ и составляет из этих чисел музыкальную пропорцию (6.7):

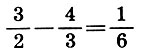
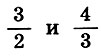
Произведение средних членов этой пропорции равно данному числу 2, а их разность меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно, можно рассматривать как приближенные значения .

Проделав ту же процедуру над первыми приближениями, получим вторые приближения:

а затем — и третьи приближения:

Поскольку данную процедуру можно повторять неограниченно, то ясно, что число иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение равно 1,414213. мы видим, что «музыкальный» метод Архита очень быстро сходится к точному значению и уже третье приближение дает пять верных знаков после запятой!

* (Интервал тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами.)

Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:

дорийский: полутон — тон — тон;

фригийский: тон — полутон — тон;

лидийский: тон — тон — полутон.

Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.

Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли «гармония». Именно в античной теории музыки слово «гармония» обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:

* («Почти» потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая.)

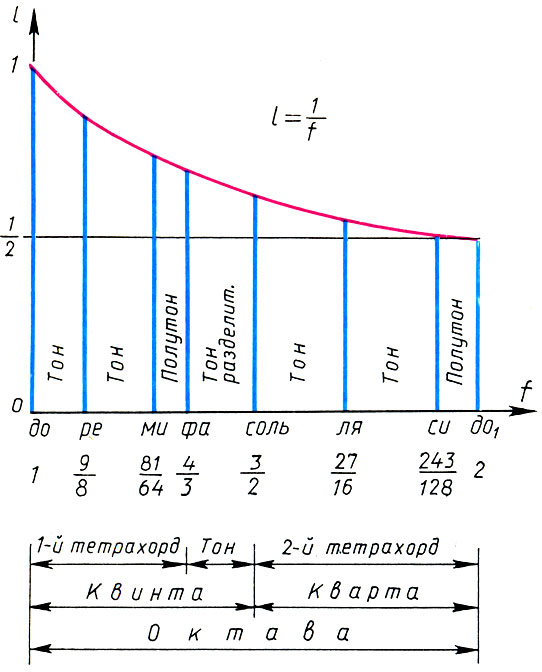
Пифагоров строй лидийской гаммы и его математические характеристики

Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f₁ = 1, oнаходим первый тетрахорд: f₁ = 1, f₂ = 9 /₈, f₃ = 9 /₈* 9 /₈= 81 /₆₄, f₄= 4 /₃. Второй тетрахорд получается сдвигом первого на квинту: f₅ = 3 /₂f_l = 3 /₂, f₆ = 3 /₂f₂ = 27 /₁₆, f₇ = 3 /₂f₃ = ₂₄₃/₁₂₈, f₈ = 3 /₂f₄ = 2. Окончательно для интервальных коэффициентов имеем

(6.14)

Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.

Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики «склеивали» тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах. Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.

Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения

Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его «этосом», устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.

Пляшущая менада. Рельеф

Так, развивая в работе «Государство» теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: «Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке». Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, «платонический» идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.

Аристотель в «Политике» судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную «этическую» классификацию ладов, различая лады, которые вызывают психическое равновесие (дорийский), напротив, нарушают его (гипофригийский — «застольный» лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).

Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского «серебряного века» профессор А. Ф. Лосев (1893-1988) * : «Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. „Веселые“ же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки… Так задумчива, печальна и благородна вся греческая скульптура».

* (Судьба Алексея Федоровича Лосева счастлива и трагична. Счастлива, потому что до последнего дня своей 95-летней жизни Лосев сохранил поразительную работоспособность и успел завершить главный труд — восьмитомную «Историю античной эстетики». Трагична, потому что другие восемь томов его сочинений, написанных на полвека ранее (1927 — 1930), были преданы анафеме, а сам автор, будучи незаконно репрессирован, продолжил свои философские изыскания на строительстве Беломорско-Балтийского канала, откуда он писал: «Я закован в цепи, когда в душе бурлят непочатые и неистощимые силы». Одна из этих работ Лосева — «Музыка как предмет логики» — могла бы служить путеводной звездой к этой книге. И все-таки судьба А. Ф. Лосева счастлива, ибо рукописи не горят. Сегодня огромное философское наследие А. Ф. Лосева обретает свое второе рождение. )

Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о «сладкой лидийской мелодии» или о «разнообразной лидийской мелодии».

До сих пор мы ничего не говорили о «самом совершенном консонансе» — приме (унисоне) (l₂/l₁ = 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость.

Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является «Песня о Родине» композитора И. О. Дунаевского (1900-1955). В ее запеве («От Москвы до самых до окраин. ») дважды звучит восходящая октава (l₁/l₂ = 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l₁/l₂ = 3/2) также звучит широко, но более рельефно и динамично, чем октава.

Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l₁/l₂ = 4/3), например «Интернационал», «Гимн Советского Союза», «Марсельеза». Здесь интервал кварты звучит решительно и активно, как призыв к действию.

Особый «этос» у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня «Во поле береза стояла» начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.

А наиболее неприятным и неблагозвучным является интервал тритон или полуоктава (l₁/l₂ = ). Своей неблагозвучностью этот интервал «подсказал» Архиту «музыкальное доказательство» иррациональности .

Источник