Что такое гамильтонов цикл

Гамильтонов цикл

Вы будете перенаправлены на Автор24

Гамильтонов цикл — это замкнутый маршрут прохождения всех вершин выбранного графа строго по одному разу.

Гамильтонов цикл

Гамильтонов цикл в графе — это такой маршрут обхода вершин графа, при котором посещается по одному разу каждая его вершина, а под гамильтоновым путём понимается незамкнутый путь, но который тоже проходит через каждую вершину графа. Построить гамильтонов цикл представляется необычайно сложной проблемой, и на сегодняшний день не существует оптимального алгоритма для разрешения этой задачи. Можно предположить, что алгоритма, который способен решить эту задачу, вероятнее всего нет. То есть это одна из задач теории сложности алгоритмов, не имеющих на сегодня решения. Возможно сформировать решение, основанное на переборе вариантов, но его сложность будет примерно равна O(n!). К примеру, если выполнить нумерацию всех вершин графа, то нумерация вершин в их последовательности в цикле Гамильтона, выполнит некую перетасовку чисел от единицы до n. Возможно выполнить перебор всех допустимых n! вариантов и для каждого из них сделать проверку соответствия искомому циклу на графе. То есть проверку, что каждая пара соседних вершин в текущем варианте, а также начальная и конечная вершина соединяются ребром. Для такой переборки вариантов возможно применить, например, известный алгоритм перебора с возвратом. Можно переписать данный алгоритм таким образом, чтобы отсекались явно неверные варианты, то есть к уже выстроенному отрезку маршрута будут прибавляться лишь те вершины, которые соединяются ребром с конечной вершиной маршрута и не посещались раньше. После прибавления новой вершины к путевому маршруту, следует сделать рекурсию, то есть запуск алгоритма из новой вершины. По многим параметрам такой алгоритм похож на поиск в глубину, но он имеет и существенное отличие. Оно состоит в том, что в случае возврата пути из какой-либо вершины на предыдущую точку, с оставленной вершины удаляется пометка о её посещении. При таком способе возможен возврат алгоритма на эту же вершину повторно, но уже другим путём. Более того, это обязательно должно произойти, в случае существования гамильтонова пути в этом графе, поскольку гамильтонов должен пройти через каждую вершину.

Рассмотрим пример. Будем считать, что n является числом вершин в графе и все вершины имеют нумерацию от нуля до n−1, а сам граф определяется с помощью матрицы смежности A. Глобальная переменная Path содержит перечень вершин, которые вошли в путевой маршрут. В функцию hamilton заносятся в виде параметров номера вершин, которые прибавляются к маршруту, и она же возвращает признак true, если построение гамильтонова пути оказалось удачным, в противном случае возвращается значение false. При этом в случае удачного построения пути, он сохранится в переменной Path.

Реализация алгоритма на языке С++

Рисунок 1. Реализация алгоритма на языке С++. Автор24 — интернет-биржа студенческих работ

Реализация алгоритма на языке PYTHON

Готовые работы на аналогичную тему

Рисунок 2. Реализация алгоритма на языке PYTHON. Автор24 — интернет-биржа студенческих работ

Функция Hamilton сначала заносит вершину curr последней в список Path. Причём, если размер списка стал равен n, что означает включение всех вершин в состав пути Path, то выполняется проверка соединения ребром первой и последней вершины (только при поиске гамильтонова цикла, для пути это не требуется) и если такое ребро есть, то возвращается значение True (цикл обнаружен). Если же такого ребра нет, то выполняется удаление из Path последней вершины и возврат значения возвращает False (цикл не обнаружен). В случае, когда размер списка менее n, делается отметка, что вершина curr посещалась, и процесс перебора продолжается далее. Поочерёдно выполняется обход всех оставшихся вершин next и в случае соединения ребром вершины next с вершиной curr, если при этом вершина next ещё не посещалась, то делается рекурсивный запуск алгоритма из вершины next с целью найти путь в эту вершину. И если рекурсия из вершины next закончится возвратом True, то есть удачным построением цикла, то алгоритм так же делает возврат True. В этом случае из переменной Path нет никаких удалений, и в списке Path находится весь гамильтонов цикл. Если не выбран ни один из выше указанных вариантов, то выполняется возврат вершины curr, то есть делается пометка, что она не посещалась, её удаляют из окончания списка Path и алгоритм возвращается к обработке последней вершины в списке Path. Следует отметить, что алгоритмическая сложность этого метода будет не меньше, чем n!, и это означает непригодность данного алгоритма для графов большого объёма.

Задача работы коммивояжёра

Задачей, аналогичной и близкой по смыслу процедуре определения гамильтонова цикла, считается задача работы коммивояжёра. Условие задачи следующее. Странствующий торговец, именуемый коммивояжёром, должен объехать n городов и возвратиться к дому. Коммивояжёр не намерен приезжать в каждый город более чем один раз и желает, чтобы маршрут его перемещений был оптимальным, то есть самым коротким из возможных. Это означает поиск внутри неориентированного взвешенного графа маршрута (пути), который обладает наименьшим весом (стоимостью). Проблему коммивояжёра возможно решить по аналогии с задачей гамильтонова цикла (пути), но в этом случае необходимо сделать перебор всех возможных маршрутов. При зацикливании пути необходимо определить его суммарный вес и выполнить сравнение найденного маршрута с весом предыдущего самого лучшего известного маршрута. Оптимально эту операцию выполнять не при окончании замыкания, а единовременно с прибавлением очередной вершины прибавлять вес рассматриваемого ребра, как выстроенного компонента маршрута.

Источник

Молчание — золото: доказательство существования Гамильтонова цикла в графе

Заменив такую сложную конструкцию плоским графом, изоморфным исходному, получим задачу, которую далее рассмотрим в системе протоколов с нулевым разглашением.

Доказательство с нулевым разглашением

Очень убедительное (но не абсолютно определенное) свидетельство, что теорема верна, и что доказывающий знает это самое доказательство, дает интерактивный вероятностный протокол, называющийся доказательством с нулевым разглашением.

Интерактивность в данном определении говорит о том, что стороны общаются в течение нескольких раундов. В стандартных математических доказательствах имеет место только один вид взаимодействия: доказывающий дает проверяющему доказательство «на проверку», и на этом все заканчивается. В нашем же случае процесс доказательства утверждения превращается в разговор, который заканчивается убеждением проверяющего (если все идет хорошо).

Как убедить кого-то в существовании Гамильтонова цикла, не раскрывая сам цикл

Пусть обеим сторонам известен некоторый граф , вершины которого пронумерованы от до . Необходимо доказать проверяющему существование цикла в G, который посещает каждую вершину ровно один раз.

На вход системе с нулевым разглашением мы подаем, где — положительное целое число, которое играет роль параметра безопасности и является количеством последовательных взаимодействий между сторонами: чем больше , тем больше уверенность проверяющего в доказательстве.

Дальнейшие шаги будут выполняться раз.

Доказывающая сторона выбирает случайную перестановку чисел и рисует матрицу смежности для графа, помечая строки и столбцы в соответствии с этой перестановкой. Получается новый граф, изоморфный исходному, построенный по данной матрице, если бы нумерация строк и столбцов у нее шла в естественном порядке.

Проще говоря, мы заменяем исходный граф на его изоморфную копию.

Приватное состояние матрицы, доступное только доказывающей стороне. Публичное состояние матрицы, известное обеим сторонам.

Проверяющая сторона получает скрытую матрицу и делает выбор:

Попросить доказывающую сторону открытьсетки, соответствующих ребрам цикла Гамильтона. Процесс раскрытия симметричен: если показана запись в матрице, доказывающая сторона должна также показать запись.

C другой стороны, можно попросить доказывающую сторону открыть граф целиком.

Результат для проверяющей стороны в первом случае будет выглядеть, например, так:

Наличие 1 во всех открытых квадратах говорит о существовании ребер между соответствующими вершинами графа. Так как мы открывали по условию те квадраты, которые отвечают ребрам цикла Гамильтона, получаем доказательство существования такого цикла в графе.

Если проверяющий имел бы возможность обращаться к доказывающему только с первой просьбой, последний мог бы его легко обмануть, и, не зная Гамильтонова цикла исходного графа G, мог бы подменить его на другой с тем же количеством вершин, в котором сам знал бы цикл. Короче говоря, проверяющий, прося показать весь граф целиком, хочет убедиться в том, что он действительно изоморфен исходному.

Выбор того, что проверяющий будет просить у доказывающего, на каждом шаге определяется «подбрасыванием монетки».

Если все в порядке, проверяющая сторона принимает доказательство.

Если же первом случае проверяющая сторона увидит в открытых квадратах 0, она поймет, что доказывающая сторона не владеет знанием о цикле Гамильтона. Аналогично, по описанной выше причине, проверяющая сторона во втором случае тоже может понять, что доказывающий пытается ее обмануть, и в итоге она отклонит доказательство.

Докажем, что проверяющая сторона, благодаря разговору, не может получить никакой «лишней» информации.

Может показаться, что в первом случае проверяющему предоставляется знание, благодаря которому он способен самостоятельно полностью узнать доказательство.

Это было бы верно, если бы он знал перестановку вершин, переводящую шифрованный граф в исходный, но поскольку за один раунд можно обратиться только с одной просьбой, и каждый раз изоморфная копия G меняется, то найти перестановку – дело безнадёжное – это значило бы решить проблему изоморфизма графов.

Что и требовалось доказать.

Заключение

Рассмотрим задачу аутентификации субъекта. Она состоит в проверке подлинности одной стороны другой, например, при входе в операционную систему пользователь может доказывать свою лигитимность вводом пароля.

Если решать ее таким простым способом, то гарантия того, что он не попадет в руки злоумышленников, не очень велика.

Конечно, при таком условии нельзя быть абсолютно уверенным в том, что аутентификация субъекта будет стопроцентной. Но проверяющий каждый раз может запросить любую часть информации, причём несколько раз. К тому же, можно использовать при этом Гамильтоновы циклы, получая относительно надёжную систему доступа, ведь вероятность в каждом раунде успешно обманывать проверяющую сторону равна 1/2^k, где k – число взаимодействий сторон.

Материал подготовлен при использовании литературы:

Manuel Blum «How to Prove a Theorem So No One Else Can Claim It«

Шнайер Б. Прикладная криптография, 2-е издание: протоколы, алгоритмы, исходные тексты на языке Си //Под редакцией ПВ Семьянова. М., Триумф. – 2002.

Источник

Цикл Гамильтона

Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом (см. Словарь терминов теории графов).

Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру, узловые вершины которого символизировали крупнейшие города Земли, а рёбра — соединяющие их дороги.

Содержание

Условия существования

Условие Дирака (англ.) (1952)

Пусть p — число вершин в данном графе; если степень каждой вершины не меньше, чем 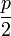, то граф называется графом Дирака. Граф Дирака — гамильтонов.

Условие Оре (1960)

p — количество вершин в данном графе. Если для любой пары несмежных вершин x,y выполнено неравенство 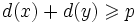, то граф называвается графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Граф Оре — гамильтонов.

Доказана теорема Бонди-Хватала (англ.), обобщающая утверждения Дирака и Оре. Вначале определим замыкание графа. Пусть у графа G n вершин. Тогда замыкание cl(G) однозначно строится по G добавлением для всех несмежных вершин u и v, у которых выполняется degree(v) + degree(u) ≥ n нового ребра uv.

Граф является гамильтоновым тогда и только тогда, когда его замыкание — гамильтонов граф.

Условие Поша

Введем следующую функцию f(x) целого неотрицательного аргумента x на графе G = [A,B] :

.

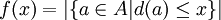
См. также

Ссылки

-> методы решения Гамильтоновых графов:

Полезное

Смотреть что такое «Цикл Гамильтона» в других словарях:

Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Цикл в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Длина пути в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Дуга (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Инцидентность — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Мультиграф — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Подграф — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

Применение алгоритма Гровера для поиска гамильтоновых циклов в графе

1. Введение

В данной статье представлен вариант применения квантового алгоритма Гровера для решения задачи поиска гамильтоновых циклов в графе.

Сразу отмечу, что данный вариант решения задачи является учебным. Он не даст так называемого «квантового превосходства», поскольку при росте числа вершин в графе, нам потребуется большее число кубит, циклов Гровера и запусков самого алгоритма. Однако, считаю, что данный вариант заслуживает внимания, возможно он вдохновит кого-либо на поиск более оптимального решения.

2. Постановка задачи

Представим, что существует граф, состоящий из пяти вершин O, A, B, C, D, и восьми ребер. Вершину O мы будем считать исходной точкой.

Граф из 5 вершин

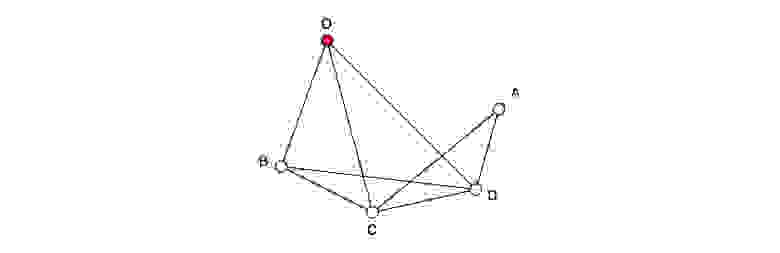
Некий путник, который находится в точке O, хочет пройти через все вершины графа, зайти в каждую из них только один раз и вернуться снова в исходную точку O. Необходимо найти все возможные маршруты путника, удовлетворяющие условиям задачи.

Решение этой задачи легко найти самостоятельно. Всего существуют 4 варианта такого пути, при том, что два из них являются обратными последовательностями двух других:

Гамильтоновы циклы в графе (2)

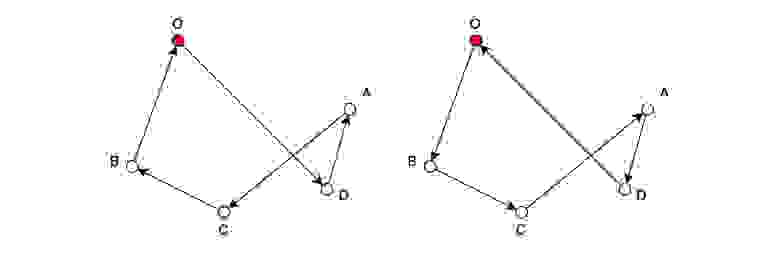
Путнику, находящемуся в исходной точке O, необходимо совершить 5 шагов. На каждом из шагов путник переходит по связывающему ребру из одной вершины в другую. Все посещенные вершины должны быть уникальны для маршрута, кроме точки O, в ней путник оказывается дважды, поскольку последний 5-ый шаг должен привести его на исходную позицию.

Маршрутом мы будем называть последовательность вершин, через которые должен пройти путник, например: OBCADO. Каким бы ни был маршрут (последовательность вершин), он должна удовлетворять следующим правилам:

вершины маршрута должны быть уникальны, путник дважды не заходит в один и тот же пункт;

переход на любом шаге маршрута возможен только в ту вершину, которая связана с текущей:

маршрут начинается и заканчивается в точке O, поэтому для простоты мы исключим ее из маршрута, оставим только изменяющуюся часть — 4 вершины.

Как будем решать?

Решить данную задачу можно в лоб, методом перебора. Итак, мы будем перебирать 4 * 4 * 4 * 4 = 256 комбинации вершин:

При переборе нам необходимо определить, удовлетворяет ли рассматриваемый в конкретный момент маршрут условиям задачи. Рассмотрим несколько примеров.

Допустим, мы рассматриваем маршрут ADCB. Он невозможен для путника, поскольку первый шаг должен быть из точки O в одну из вершин, соединенных с этой точкой. Вершина A не соединяется с точкой O, такой маршрут мы должны отбросить.

Другой пример, маршрут CAAB — его также необходимо отбросить, поскольку в нем путнику придется дважды зайти в вершину A.

Еще пример, маршрут BACD, тоже отбрасываем, путник никак не может попасть из вершины B сразу в вершину A (второй шаг), так как эти вершины не связаны.

Итак, нам необходимо перебрать 256 комбинаций, из которых следует отбрасывать те, в которых:

повторяется хотя бы одна из вершин

любые две соседние вершины в комбинации не связаны ребром

первая в комбинации вершина не связана с исходной точкой O

последняя в комбинации вершина не связана с исходной точкой O

Решить данную задачу можно в цикле на обычном ПК, однако, мы преследуем учебные цели и хотим разработать решение для квантового компьютера. Для этого будем использовать квантовый алгоритм Гровера.

Выразим маршрут и вершины на языке кубит.

Возьмем 8 кубит, разобьем их условно на 4 пары. Первая пара соответствует первой вершине пути, вторая пара — второй вершине, и т.д. В каждой паре кубит возможна одна из 4-х комбинаций кубит: 00, 01, 10, 11. Положим, что каждой из этих комбинаций соответствует одна из возможных вершин: A, B, C, D:

Рассмотренные ранее комбинации ADCB, CAAB и BACD будут соответствовать следующим комбинациям кубит: 00111001, 10000001 и 01001011 соответственно.

Если мы применим к этим восьми кубитам оператор Адамара, то получим суперпозицию из всех возможных вариантов движения путника, то есть все 256 комбинаций. Далее в оракуле нам необходимо реализовать процедуры, которые будут проверять эти комбинации на соответствие условиям задачи.

Однако, еще до реализации оракула мы можем воспользоваться одной хитростью, которая позволит нам сократить число комбинаций почти в два раза.

3. Суперпозиция

Самым первым шагом большинства квантовых алгоритмов является создание суперпозиции всех входных кубитов. Однако, мы можем тут отойти от традиции и применить небольшую хитрость, которую применили авторы этой статьи. Суть хитрости заключается в следующем: если нам известны невозможные комбинации кубит, мы можем их заранее исключить из суперпозиции.

Поскольку 1-ый шаг совершается из точки O, и первая вершина должна быть связана с этой точкой, значит это не может быть вершина A, это могут быть только вершины B, C или D. Аналогично, последний 5-ый шаг совершается из 4-ой вершины в точку O, и она должна быть связана с точкой O, значит это не может быть вершина A.

Раз первая вершина в маршруте может быть только вершиной B, C или D, то и первая пара кубит, соответствующая первой вершине в маршруте путника, может принимать только следующие значения: 01, 10 и 11. Это же справедливо и для последней пары кубит, соответствующей четвертой вершине маршрута.

Таким образом, мы исключим из суперпозиции ненужную комбинацию 00 (вершину A) для первой и четвертой вершины и, благодаря этому нам уже не потребуется в оракуле проводить проверку на связь этих вершин с точкой O, и мы сократим число комбинаций до 3 * 4 * 4 * 3 = 144.

Итак, рассмотрим, как работает этот прием для пары кубит.

Начальное состояние системы из двух кубит запишем следующим образом:

Выполним ряд преобразований.

Шаг 1. Подействуем на первый кубит оператором

с таким углом , при котором матрица оператора принимает следующий вид:

Не будем для угла искать «красивое» значение, положим его равным:

Посмотрим, как этот оператор подействует на первый кубит :

После действия оператора на первый кубит пары мы получим следующую суперпозицию 2-х кубит:

Шаг 2. Подействуем на второй кубит контролируемым вентилем Адамара

Контролируемый вентиль Адамара изменяет второй кубит только тогда, когда первый кубит равен

Шаг 3. Подействуем на второй кубит вентилем NOT

Ко второму кубиту применим вентиль NOT:

Итак, мы получили суперпозицию, в которой отсутствует комбинация 00.

После того, как мы подробно разобрали теоретическую часть, приступим к написанию соответствующей процедуры. Библиотека qiskit имеет в своем арсенале все вентили, приведенные в теоретической части:

Однокубитный вентиль — QuantumCirquit.ry(theta, target_qubit)

theta — угол

target_qubit — кубит, на который воздействует вентиль

Контролируемый вентиль Адамара — QuantumCirquit.ch(control_qubit, target_qubit)

control_qubit — контролирующий кубит

target_qubit — кубит, на который воздействует вентиль

Однокубитный вентиль NOT— QuantumCirquit.x(target_qubit)

target_qubit — кубит, на который воздействует вентиль

Напишем процедуру, которая на вход будет получать пару кубит и применять к ним последовательно все перечисленные в теоретической части операторы:

Отмечу сразу, должна быть возможность выполнить данную процедуру в обратном порядке, поэтому мы ввели дополнительный аргумент reverse. О необходимости в этом подробнее расскажу позже.

Исключать возможность получить вариант A мы будем из первой и четвертой вершины маршрута. Вторая и третья вершины должны иметь все возможные варианты в суперпозиции, поэтому на них будем действовать классически — вентилем Адамара.

4. Оракул

В алгоритме Гровера оракул должен инвертировать фазу «хорошей» комбинации входящих кубит. Если комбинация удовлетворяет условиям уникальности и требованию по связанности вершин, то у такой комбинации оракул должен изменить фазу. В противном случае, если хотя бы одно из условий будет нарушено, оракул оставляет фазу неизменной.

Инверсия фазы равносильна простой инверсии результирующего кубита из в , который не является частью входных кубит маршрута. Оракул должен быть построен таким образом, чтобы для «хорошей» комбинации результирующий кубит изменял свое состояние на состояние .

По умолчанию комбинация объявляется «хорошей». Однако, если будет найдено хотя бы одного совпадение вершин или один несвязанный переход между ними, маршрут будет признан «плохим» и инверсии результирующего кубита не произойдет.

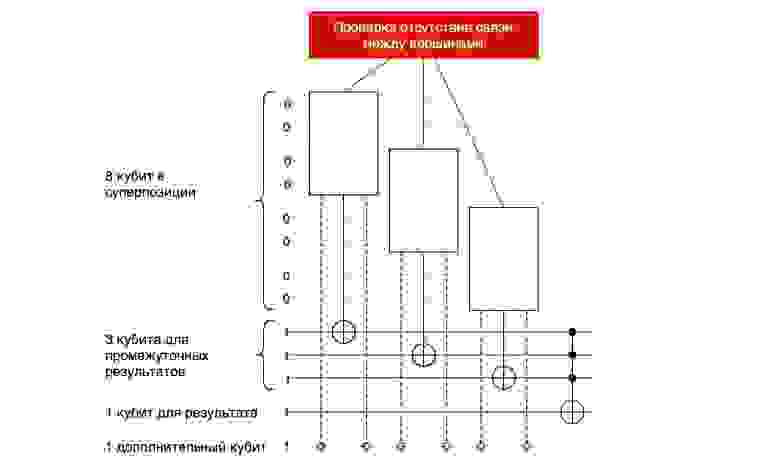
На рисунке условно изображена схема алгоритма для решения нашей задачи.

Рассмотрим детально содержание проверок на уникальность и на связанность вершин.

4.1. Контроль совпадения вершин

Задача данного блока состоит в том, чтобы не дать оракулу инвертировать результирующий кубит, если вдруг в комбинации встретятся хотя бы две одинаковых вершины.

Чтобы проверить, нет ли совпадающих вершин в комбинации, нам необходимо последовательно проверить все возможные пары вершин на равенство. Для каждой пары вершин будем проверять, не являются ли они обе одновременно либо вершинами A, либо B, либо C, либо D.

Проверка совпадения вершин

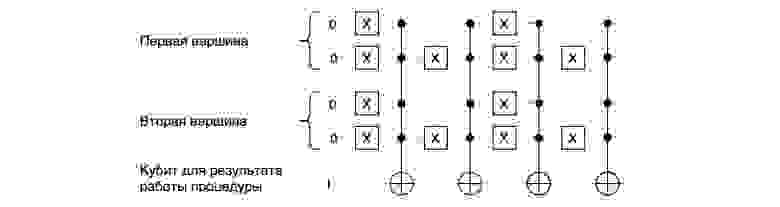
Представим, что на вход подаются две вершины A, тогда все четыре входных кубита равны 0. После применения ко всем четырем кубитам вентиля NOT они становятся равны 1. Множественный вентиль Тоффоли инвертирует результирующий кубит. Дальше в схеме кубиты будут подвержены преобразованию для проверки одновременного равенства вершинам B, C и D. Эти проверки будут неудачными и не изменят результирующий кубит, его значение останется инвертированным.

Если на вход подаются несовпадающие вершины, результирующий кубит на всех этапах схемы останется нетронутым.

Процедура проверки совпадения вершин

Напишем простую процедуру, на вход которой будем подавать две пары кубит, соответствующие двум вершинам маршрута, а также кубит, в который функция будет передавать результат проверки.

Eсли в качестве пар переданы одинаковые вершины, то процедура изменяет результирующий кубит на обратный, сигнализирует о совпадение вершин.

Полная схема «детектора совпадений» будет выглядеть примерно так:

В оракуле нам потребуется применить эту процедуру ко всем парам вершин, а поскольку у нас 4 вершины, то процедуру придется запустить 6 раз — это число сочетаний из 4-х по 2:

При восьми вершинах нам уже потребуется запустить данную функцию для 28 пар вершин. Именно эта часть алгоритма и является узким местом.

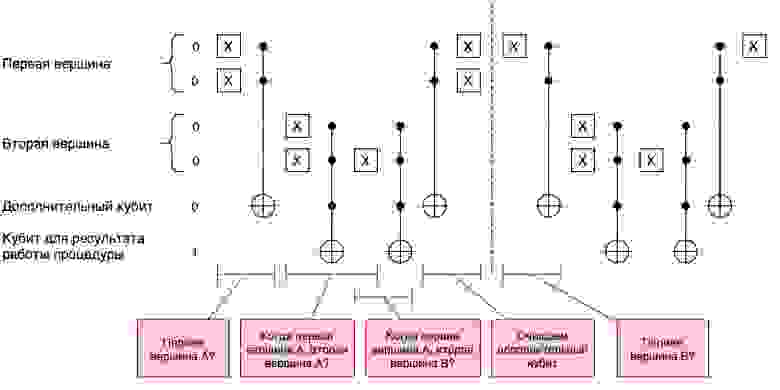
4.2. Проверка связи вершин

Задача данного блока оракула состоит в том, чтобы для всех трех пар рядом стоящих вершин определить, существует ли связывающее их ребро. Если хотя бы у одной такой пары нет связи, то процедура не позволяет оракулу, объявить комбинацию «хорошей» и изменить результирующий кубит. Изменив результирующий кубит на 0, процедура не даст оракулу объявить такой маршрут «хорошим».

Суммарная логика должна быть такая: результирующий кубит проверки на связанность вершин должен измениться (1 → 0) если хотя бы одна пара рядом стоящих вершин не будет связана ребром.

Как мы будем решать эту задачу?

Допустим мы проверяем 3-ю и 4-ю вершины маршрута. И допустим, 3-я вершина есть вершина A. Но мы знаем, что из вершины A можно попасть только в вершины C и D. Следовательно, сначала нужно проверить, выпала ли на 3-ем шаге вершина A, и если это так, то проверить, какая вершина следующая. Нам необходимо выявить именно негативные случаи, когда следующая 4-ая вершина не является ни вершиной C, ни D, и только в этом случае объявить комбинацию неудачной. Проверить это мы сможем от обратного, если 4-ая вершина является вершиной A или B (логически эквивалентно «ни C, ни D»), то считаем текущую комбинацию неудачной. Такая «обратная» форма для нас проще в реализации и позволит сократить число дополнительных кубит.

Не забываем про то, что нам необходимо провести аналогичные проверки для всех остальных случаев, когда третья вершина есть B, C или D. А также для всех возможных пар рядом стоящих вершин в маршруте.

Приступим к реализации данной процедуры. На вход ей будем подавать один кубит для результата и две пары кубит двух вершин. Первую будем называть основной, вторую — соседней.

Мы будем последовательно проверять, какой вершиной (A, B, C или D) является основная вершина. Для этого нам потребуется вентиль Тоффоли. Далее для каждой из возможных ситуаций будем проверять соседнюю вершину на предмет того, является ли она связанной с основной вершиной.

Логика работы процедуры следующая:

Проверяем, является ли основная вершина вершиной A, если верно, то проверяем:

Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.

Проверяем, является ли основная вершина вершиной B, если верно, то проверяем:

Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.

Проверяем, является ли основная вершина вершиной C, если верно, то проверяем:

Является ли соседняя вершина любой, то инвертируем результирующий кубит (условие всегда выполняется).

Проверяем, является ли основная вершина вершиной D, если верно, то далее логика аналогична логике с вершиной C.

Давайте детально рассмотрим алгоритм описанных выше проверок.

Сначала проверяем, является ли основная вершина вершиной A.

Но каким образом мы можем это проверить? Вершина A в виде кубит имеет представление 00, мы можем к обоим кубитам применить вентиль NOT, тогда пара станет равной 11. Далее мы направляем эту пару в вентиль Тоффоли в качестве контролирующих кубит, он инвертирует дополнительный кубит (0 → 1). Если основная вершина не является вершиной A, то дополнительный кубит останется неизменным. Если же равна — то дополнительный кубит будет инвертированным.

Далее, нам необходимо проверить соседнюю вершину на предмет равенства вершине A или B. Для этого мы вводим дополнительный кубит для сохранения промежуточного результата проверки, применяем множественный вентиль Тоффоли к двум кубитам проверяемой вершины, но также в качестве контрольного кубита подаем в вентиль дополнительный кубит с результатом проверки на равенство основной вершины вершине A. В случае успеха вентиль Тоффоли инвертирует кубит промежуточного результата проверки.

С теоретической частью закончили, приступаем к написанию процедуры.

Сначала составим общий список вершин, заодно зафиксируем для вершин представления в кубитах:

Зафиксируем все связи вершин (кроме точки O).

Создадим справочник функций, который при подаче на вход вершины, соответствующей ключу в словаре, на выходе выдаст пару кубит 11. Вместе с вентилем Тоффоли этот справочник можно использовать как условный оператор.

Далее, создадим процедуру, которая в качестве аргументов получает две пары кубит, основной и соседней вершины, и проверяет наличие связи между ними. Также в процедуру передаем результирующий кубит, который заранее подготовлен в состоянии .

Эта процедура проверяет одну пару рядом стоящих вершин на предмет существования связи между ними. Если подобной связи нет, то она инвертирует результирующий кубит (1 → 0) процедуры, что не позволит оракулу объявить данную комбинацию «хорошей».

5. Оператор диффузии

Пример действия оператора на вектор :

Пример действия оператора на любой другой вектор:

«Сочинять» конфигурацию вентилей для оператора диффузии нет необходимости, он уже разработан. Для набора из n кубит оператор будет выглядеть следующим образом:

Оператор диффузии Гровера

Теперь напишем функцию, которая выражает оператор диффузии Гровера. Функцию сделаем универсальной, она на вход будет принимать любое количество кубит.

В качестве центрального элемента оператора используется один из трех вентилей:

когда на вход поступают всего 2 кубита — простой вентиль CNOT

когда 3 кубита — вентиль Тоффоли

когда 4 и более кубита — вентиль Тоффоли для многих кубит

Доработка оператора диффузии Гровера

Поскольку для создания начальной суперпозиции входных кубит мы не везде использовали однокубитный вентиль Адамара, нам потребуется видоизменить оператор диффузии.

В первоначальном виде оператор диффузии Гровера на входе применяет ко всем входным кубитам вентиль Адамара, тем самым как бы возвращая кубиты из суперпозиции в обычное несвязанное состояние. На выходе оператор снова применяет вентили Адамара для создания суперпозиции.

Однако, на шаге создания суперпозиции мы применили специальные операторы для исключения ненужных комбинаций из первой и четвертой пары кубит, а вентиль Адамара применили только ко второй и третьей.

Соответственно, для нашего алгоритма мы отключим в операторе диффузии Гровера входные и выходные вентили Адамара:

Теперь он выглядит так:

Адаптированный под задачу оператор диффузии Гровера

А перед вызовом оператора будем применять преобразование, обратное созданию суперпозиции, после оператора — снова создание суперпозиции:

Тут нам и пригодилась инверсная версия процедуры исключения комбинации 00 из суперпозиции.

5. Собираем все вместе

Мы не будем подробно рассматривать принципы работы алгоритма Гровера с его учебными примерами, а сразу приступим к его реализации. Рассчитаем число итераций, пусть n — число входных кубит для оракула, в нашем случае оно равно 8, тогда количество итераций алгоритма Гровера должно быть следующим:

То есть, нам потребуется всего 2 итерации алгоритма для получения отчетливого результата.

5.1. Общая схема

Все составляющие алгоритма мы рассмотрели, начинаем сборку элементов в единую рабочую цепь. Общая схема выглядит следующим образом:

Общая схема цепи

Скачиваем и устанавливаем библиотеки Qiskit, NumPy и Matplotlib для Python.

Импортируем необходимые библиотеки.

Заранее подготовим процедуру поиска совпадений вершин.

Заводим необходимые для работы переменные и вспомогательные функции:

Готовим процедуру поиска несвязанных вершин и оператор диффузии.

Подготавливаем процедуру для исключения ненужных вершин из суперпозиции:

Теперь необходимо решить, сколько нам всего потребуется кубит:

Источник