Что такое дзета функция римана

Доступное объяснение гипотезы Римана

Посвящается памяти Джона Форбса Нэша-младшего

Вы ведь помните, что такое «простые числа»? Эти числа не делятся ни на какие другие, кроме самих себя и 1. А теперь я задам вопрос, которому уже 3000 лет:

Введение

Свойства простых чисел изучались многими великими людьми в истории математики. С первого доказательства бесконечности простых чисел Евклида до формулы произведения Эйлера, связавшей простые числа с дзета-функцией. От формулировки теоремы о простых числах Гаусса и Лежандра до её доказательства, придуманного Адамаром и Валле-Пуссеном. Тем не менее, Бернхард Риман до сих пор считается математиком, сделавшим единственное крупнейшее открытие в теории простых чисел. В его опубликованной в 1859 году статье, состоявшей всего из восьми страниц, были сделаны новые, ранее неизвестные открытия о распределении простых чисел. Эта статья по сей день считается одной из самых важных в теории чисел.

После публикации статья Римана оставалась главным трудом в теории простых чисел и на самом деле стала основной причиной доказательства в 1896 году теоремы о распределении простых чисел. С тех пор было найдено несколько новых доказательств, в том числе элементарные доказательства Сельберга и Эрдёша. Однако до сих пор остаётся загадкой гипотеза Римана о корнях дзета-функции.

Сколько всего простых чисел?

Давайте начнём с простого. Все мы знаем, что число является или простым, или составным. Все составные числа состоят из простых и могут быть разложены на их произведения (a x b). В этом смысле простые числа являются «строительными блоками» или «фундаментальными элементами» чисел. В 300 году до нашей эры Евклид доказал, что их количество бесконечно. Его изящное доказательство имеет следующий вид:

Предположим, что множество простых чисел не бесконечно. Создадим список всех простых чисел. Тогда P пусть будет произведением всех простых чисел списка (перемножим все простые числа из списка). Прибавим к результату 1: Q = P +1. Как и все числа, это натуральное число Q должно быть или простым, или составным:

Почему простые числа так сложно понять?

Сам факт того, что любой новичок понимает изложенную выше задачу, красноречиво говорит о её сложности. Даже арифметические свойства простых чисел, несмотря на активное изучение, плохо нами понимаются. Научное сообщество настолько уверено в нашей неспособности понимать поведение простых чисел, что разложение на множители больших чисел (определение двух простых чисел, произведением которых является число) остаётся одной из фундаментальных основ теории шифрования. На это можно смотреть следующим образом:

Мы хорошо понимаем составные числа. Это все числа, не являющиеся простыми. Они состоят из простых чисел, но мы можем с лёгкостью написать формулу, прогнозирующую и/или генерирующую составные числа. Такой «фильтр составных чисел» называется решетом. Самым знаменитым примером является так называемое «решето Эратосфена», придуманное примерно в 200 году до нашей эры. Его работа заключается в том, что оно просто помечает значения, кратные каждому простому числу вплоть до заданной границы. Допустим, возьмём простое число 2, и пометим 4,6,8,10, и так далее. Затем возьмём 3, и пометим 6,9,12,15, и так далее. В результате у нас останутся только простые числа. Хоть его очень легко понять, решето Эратосфена, как вы можете представить, не особо эффективно.

Одной из функций, серьёзно упрощающих нашу работу, будет 6n ± 1. Эта простая функция выдаёт все простые числа, за исключением 2 и 3, и удаляет все числа, кратные 3, а также все чётные числа. Подставим n = 1,2,3,4,5,6,7 и получим следующие результаты: 5,7,11,13,17,19,23,25,29,31,35,37,41,43. Единственными не простыми числами, сгенерированными функцией, являются 25 и 35, которые можно разложить на множители 5 x 5 и 5 x 7. Следующими не простыми числами, как вы могли догадаться, будут, 49 = 7 x 7, 55 = 5 x 11, и так далее. Всё легко, правда?

Для визуального отображения этого я использовал то, что называю «лестницей составных чисел» — удобный способ показать, как расположены и сочетаются сгенерированные функцией составные числа. В первых трёх столбцах показанного ниже изображения мы видим, как красиво поднимаются по каждой лестнице составных чисел простые числа 5, 7 и 11, вплоть до значения 91. Хаос, возникающий в четвёртом столбце, показывающем, как решето убрало всё, кроме простых чисел — отличная иллюстрация того, почему простые числа так сложно понять.

Фундаментальные ресурсы

Как же это всё связано с понятием, о котором вы могли слышать — с «гипотезой Римана»? Ну если говорить просто, то чтобы больше понять о простых числах, математики в 19-м веке перестали пытаться спрогнозировать местонахождение простых чисел с абсолютной точностью, и вместо этого начали рассматривать феномен простых чисел в целом. Мастером этого аналитического подхода стал Риман, и в рамках такого подхода была создана его знаменитая гипотеза. Однако прежде чем я начну её объяснять, необходимо познакомиться с некоторыми фундаментальными ресурсами.

Гармонические ряды

Гармонические ряды — это бесконечные ряды чисел, которые впервые исследовал в 14-м веке Николай Орем. Его имя связано с концепцией музыкальных гармоник — обертонов, которые выше частоты основного тона. Ряды имеют следующий вид:

Первые члены бесконечного гармонического ряда

Орем доказал, что эта сумма является несходящейся (то есть не имеющей конечного предела; она не приближается и не стремится к какому-то определённому числу, а устремлена в бесконечность).

Дзета-функции

Гармонические ряды являются особым случаем более общего типа функций под названием дзета-функция ζ(s). Вещественная дзета-функция задаётся для двух вещественных чисел r и n:

Если подставить n = 1, то мы получим гармонический ряд, который расходится. Однако при всех значениях n > 1 ряд сходится, то есть сумма при увеличении r стремится к некому числу, а не уходит в бесконечность.

Формула произведения Эйлера

Первая связь между дзета-функциями и простыми числами была установлена Эйлером, когда он показал, что для двух натуральных (целочисленных и больше нуля) чисел n и p, где p является простым, справедливо следующее:

Произведение Эйлера для двух чисел n и p, где оба больше нуля, а p является простым.

Это выражение впервые появилось в статье 1737 года под названием Variae observationes circa series infinitas. Из выражения следует, что сумма дзета-функции равна произведению величин, обратной единице, минус величина, обратная простым числам в степени s. Эта потрясающая связь заложила фундамент современной теории простых чисел, в которой с тех пор дзета-функция ζ(s) начала использоваться как способ изучения простых чисел.

Доказательство формулы — это одно из самых любимых моих доказательств, поэтому я изложу его, хоть для наших целей это и не обязательно (но настолько же оно прекрасно!):

Доказательство формулы произведения Эйлера

Эйлер начинает с общей дзета-функции

Сначала он умножает обе части на второй член:

Дзета-функция, умноженная на 1/2 s

Затем он вычитает получившееся выражение из дзета-функции:

Он повторяет этот процесс, далее умножая обе стороны на третий член

А затем вычитает получившееся выражение из дзета-функции

Если повторять этот процесс до бесконечности, в конце концов у нас останется выражение:

1 минус все величины, обратные простым числам, умноженное на дзета-функцию

Если этот процесс вам знаком, то это потому, что Эйлер по сути создал решето, очень похожее на решето Эратосфена. Он отфильтровывает из дзета-функции числа, не являющиеся простыми.

Затем разделим выражение на все его члены, являющимися обратными простым числам величинами, и получим:

Функциональная связь дзета-функции с простыми числами для первых простых чисел 2,3,5,7 и 11

Упростив выражение, мы показали следующее:

Формула произведения Эйлера — равенство, показывающее связь между простыми числами и дзета-функцией

Разве это было не красиво? Подставим s = 1, и найдём бесконечный гармонический ряд, повторно доказав бесконечность простых чисел.

Функция Мёбиуса

Август Фердинанд Мёбиус переписал произведение Эйлера, создав новую сумму. Кроме величин, обратных простым числам, функция Мёбиуса также содержит каждое натуральное число, являющееся произведением чётного и нечётного количества простых множителей. Числа, исключённые из его ряда — это такие числа, которые делятся на какое-то простое число в квадрате. Его сумма, обозначаемая как μ(n), имеет следующий вид:

Функция Мёбиуса — изменённая версия произведения Эйлера, заданная для всех натуральных чисел

Сумма содержит величины, обратные:

Ряд/сумма единиц, разделённых на дзета-функцию ζ(s)

Сумма не содержит те обратные величины, которые делятся на квадрат одного из простых чисел, например, 4,8,9, и так далее.

Три возможных значения функции Мёбиуса μ(n)

Хотя впервые эта хитрая сумма была формально определена Мёбиусом, примечательно, что за 30 лет до него об этой сумме писал в заметках на полях Гаусс:

«Сумма всех первообразных корней (простого числа p) или ≡ 0 (когда p-1 делится на квадрат), или ≡ ±1 (mod p) (когда p-1 является произведением неравных простых чисел); если их количество чётно, то знак положителен, но если количество нечётно, то знак отрицателен».

Функция распределения простых чисел

Вернёмся к простым числам. Чтобы понять, как распределяются простые числа при движении вверх по числовой прямой, не зная точно, где они находятся, полезно будет подсчитать, сколько их встречается до определённого числа.

Именно эту задачу выполняет предложенная Гауссом функция распределения простых чисел π(x): она даёт нам количество простых чисел, меньших или равных заданному вещественному числу. Поскольку мы не знаем формул для нахождения простых чисел, формула распределения простых чисел известна нам только как график, или ступенчатая функция, увеличивающаяся на 1, когда x является простым числом. На графике ниже показана функция до x = 200.

Функция распределения простых чисел π(x) до значения x = 200.

Теорема о распределении простых чисел

Теорема о распределении простых чисел, сформулированная Гауссом (и независимо от него Лежандром), гласит:

Теорема о распределении простых чисел

Обычным языком это можно изложить так: «При движении x к бесконечности функция распределения простых чисел π(x) будет приближаться к функции x/ln(x)». Другими словами, если забраться достаточно далеко, и график распределения простых чисел поднимется до очень высокого числа x, то при делении x на натуральный логарифм x соотношение этих двух функций будет стремиться к 1. Ниже на графике показаны две функции для x = 1000:

Функция распределения простых чисел π(x) и приблизительная оценка по теореме распределения простых чисел до x = 1000

С точки зрения вероятностей, теорема о распределении простых чисел гласит, что если случайным образом выбрать натуральное число x, то вероятность P(x) того, что это число будет простым, примерно равно 1 / ln(x). Это означает, что средний разрыв между последовательными простыми числами среди первых x целочисленных значений приблизительно равен ln(x).

Интегральный логарифм

Функция Li(x) определена для всех положительных вещественных чисел, за исключением x = 1. Она задаётся интегралом от 2 до x:

Интегральное представление функции интегрального логарифма

Построив график этой функции рядом с функцией распределения простых чисел и формулой из теоремы о распределении простых чисел, мы видим, что Li(x) на самом деле является лучшим приближением, чем x/ln(x):

Интегральный логарифм Li(x), функция рапределения простых чисел π(x) и x/ln(x) на одном графике

Чтобы узнать, насколько лучше это приближение, мы можем построить таблицу с большими значениями x, количеством простых чисел до x и величиной погрешности между старой (теорема о распределении простых чисел) и новой (интегральный логарифм) функциями:

Количество простых чисел до заданной степени десятки и соответствующие погрешности для двух приближений

Как легко можно заметить, интегральный логарифм намного лучше в приближении, чем функция из теоремы о распределении простых чисел, он «ошибся» в большую сторону всего на 314 890 простых чисел для x = 10 в степени 14. Тем не менее, обе функции сходятся к функции распределения простых чисел π(x). Li(x) сходится гораздо быстрее, но при стремлении x к бесконечности соотношение между функцией распределения простых чисел и функциями Li(x) и x/ln(x) приближается к 1. Покажем это наглядно:

Схождение соотношений двух приближенных значений и функции распределения простых чисел к 1 при x = 10 000

Гамма-функция

Гамма-функция Γ(z) стала важным объектом для изучения с тех пор, когда в 1720-х годах Даниил Бернулли и Христиан Гольдбах исследовали задачу обобщения функции факториала на нецелые аргументы. Это обобщение функции факториала n! (1 x 2 x 3 x 4 x 5 x …. n), сдвинутое вниз на 1:

Гамма-функция, определённая для z

Её график очень любопытен:

Гамма-функция Γ(z) определена для всех комплексных значений z больше нуля. Как вы наверно знаете, комплексные числа — это класс чисел с мнимой частью, записываемых как Re(z) + Im(z), где Re(z) — это вещественная часть (обычное вещественное число), а Im(z) — мнимая часть, обозначаемая буквой i. Комплексное число обычно записывается в виде z = σ + it, где сигма σ — вещественная часть, а it — мнимая. Комплексные числа полезны тем, что они позволяют математикам и инженерам работать с задачами, недоступными обычным вещественным числам. В графическом виде комплексные числа расширяют традиционную одномерную числовую прямую в двухмерную числовую плоскость, называемую комплексной плоскостью, в которой вещественная часть комплексного числа откладывается по оси x, а мнимая — по оси y.

Чтобы гамма-функцию Γ(z) можно было использовать, её обычно переписывают в виде

Функциональная связь гамма-функции Γ(z)

С помощью этого равенства мы можем получить значения для z ниже нуля. Однако оно не даёт значений для отрицательных целых чисел, потому что они не определены (формально они являются вырожденностями или простыми полюсами).

Дзета и гамма

Связь между дзета-функцией и гамма-функцией задаётся следующим интегралом:

Дзета-функция Римана

Ознакомившись со всеми необходимыми фундаментальными ресурсами, мы можем наконец приступать к установлению связи между простыми числами и гипотезой Римана.

Немецкий математик Бернхард Риман родился в 1826 году в Брезеленце. Будучи студентом Гаусса, Риман опубликовал работу в области математического анализа и геометрии. Считается, что наибольший вклад он внёс в области дифференциальной геометрии, где заложил фундамент языка геометрии, позже использованного Эйнштейном в общей теории относительности.

Его единственный труд в теории чисел, статья 1859 года Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse («О простых числах меньше заданной величины») считается самой важной статьёй в этой области математики. Всего на четырёх страницах он изложил:

Дзета-функция Римана

Мы видели тесную связь между простыми числами и дзета-функцией, показанную Эйлером в его произведении. Однако за исключением этой связи об их взаимоотношениях было мало что известно, и чтобы показать их, потребовалось изобретение комплексных чисел.

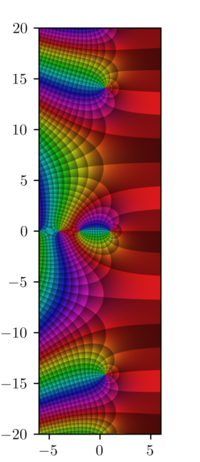
Риман первым рассмотрел дзета-функцию ζ(s) для комплексной переменной s, где s = σ + it.

Дзета-функция Римана для n, где s = σ + it — это комплексное число, в котором σ и t являются вещественными числами.

Этот бесконечный ряд, названный дзетой-функцией Римана ζ(s), является аналитическим (то есть имеет определяемые значения) для всех комплексных чисел с вещественной частью больше 1 (Re(s) > 1). В этой области определения он сходится абсолютно.

Чтобы проанализировать функцию в областях за пределами обычной области сходимости (когда вещественная часть комплексной переменной s больше 1), функцию нужно переопределить. Риман успешно с этим справился, выполнив аналитическое продолжение до абсолютно сходящейся функции на полуплоскости Re(s) > 0.

Переписанный вид дзета-функции Римана, где = x — |x|

Это новое определение дзета-функции аналитично в любой части полуплоскости Re(s) > 0, за исключением s = 1, где она является вырожденностью/простым полюсом. В этой области определения она называется мероморфной функцией, потому что она голоморфна (комплексно дифференцируема в окрестности каждой точки в области её определения), за исключением простого полюса s = 1. Кроме того, она является превосходным примером L-функции Дирихле.

В своей статье Риман на этом не остановился. Он перешёл к аналитическому продолжению своей дзета-функции ζ(s) на всю комплексную плоскость, воспользовавшись гамма-функцией Γ(z). Чтобы не усложнять пост, я не буду приводить эти вычисления, но крайне рекомендую вам посмотреть их самостоятельно, чтобы убедиться в удивительной интуиции и мастерстве Римана.

В его методе используется интегральное представление гаммы Γ(z) для комплексных переменных и тета-функции Якоби ϑ(x), которые можно переписать таким образом, чтобы появилась дзета-функция. Решая относительно дзета, получаем:

Функциональное уравнение дзеты для всей комплексной плоскости за исключением двух вырожденностей при s = 0 и s = 1

В таком виде мы замечаем, что член ψ(s) уменьшается быстрее чем любая степень x, а значит, интеграл сходится ко всем значениям s.

Зайдя ещё дальше, Риман заметил, что первый член в скобках (-1 / s(1 — s) ) является инвариантом (не меняется), если заменить s на 1 — s. Благодаря этому Риман ещё больше расширил полезность уравнения, устранив два полюса в s=0 и s=1, и задав кси-функцию Римана ξ(s) без вырожденностей:

Кси-функция Римана ξ(s)

Нули дзета-функции Римана

Корни/нули дзета-функции, когда ζ(s)=0, можно разделить на два вида, которые называются «тривиальными» и «нетривиальными» нулями дзета-функции Римана.

Существование нулей с вещественной частью Re(s) 1

Из формулировки дзеты Эйлера мы можем мгновенно увидеть что дзета ζ(s) не может быть нулём в области с вещественной частью s больше 1, потому что сходящееся бесконечное произведение может быть нулём только если равен нулю один из его множителей. Доказательство бесконечности простых чисел отрицает это.

Формула произведения Эйлера

Существование нулей с вещественной частью 0 ≤ Re(s) ≤ 1

Мы нашли тривиальные нули дзеты в отрицательной полуплоскости, когда Re(s) 1 не может быть нулей.

Однако область между этими двумя областями, называемая критической полосой, была основным центром внимания аналитической теории чисел в течение последних сотен лет.

Источник

СОДЕРЖАНИЕ

Определение

Конкретные значения

Для любого положительного четного числа 2 n :

Для неположительных целых чисел

В частности, ζ обращается в нуль при отрицательных четных целых числах, потому что B _m = 0 для всех нечетных m, кроме 1. Это так называемые «тривиальные нули» дзета-функции.

С помощью аналитического продолжения можно показать, что:

Формула произведения Эйлера

В 1737 году связь между дзета-функцией и простыми числами была обнаружена Эйлером, который доказал тождество

Функциональное уравнение Римана

Для удобства пусть

так что 2 ψ ( Икс ) + 1 знак равно 1 Икс < 2 ψ ( 1 Икс ) + 1 >. <\ displaystyle 2 \ psi (x) + 1 = <1 \ over <\ sqrt >> \ left \ <2 \ psi left (<1 over x>\ right) +1 \ right \>. >

Функциональное уравнение было установлено Риманом в его статье 1859 года « О числе простых чисел меньше заданной величины » и использовалось, в первую очередь, для построения аналитического продолжения. Эквивалентное соотношение было предположено Эйлером более ста лет назад, в 1749 году, для эта-функции Дирихле (переменной дзета-функции):

Риман также нашел симметричную версию функционального уравнения, применимого к xi-функции:

Нули, критическая линия и гипотеза Римана

Первые несколько нетривиальных нулей

Нуль
1/2 ± 14,134725 и
1/2 ± 21,022040 я
1/2 ± 25,0 · 10858 я
1/2 ± 30,424876 и
1/2 ± 32,93 5062 и
1/2 ± 37,586178 я

Количество нулей в критической полосе

Гипотезы Харди – Литтлвуда

В 1914 году Годфри Гарольд Харди доказал, что ζ ( 1 / 2 + it ) имеет бесконечно много действительных нулей.

Эти две гипотезы открыли новые направления в исследовании дзета-функции Римана.

Нулевой регион

В 2015 году Моссингхофф и Трудгиан доказали, что дзета не имеет нулей в этом регионе.

Другие результаты

Известно, что на критической прямой бесконечно много нулей. Литтлвуд показал, что если последовательность ( γ _n ) содержит мнимые части всех нулей в верхней полуплоскости в порядке возрастания, то

Теорема о критической прямой утверждает, что положительная доля нетривиальных нулей лежит на критической прямой. (Гипотеза Римана подразумевает, что эта пропорция равна 1.)

ζ ( s ) знак равно ζ ( s ¯ ) ¯ <\ displaystyle \ zeta (s) = <\ overline <\ zeta (<\ overline >)>>>

Различные свойства

Взаимный

Обратная величина дзета-функции может быть выражена в виде ряда Дирихле по функции Мёбиуса μ ( n ) :

Универсальность

Оценки максимума модуля дзета-функции

Пусть функции F ( T ; H ) и G ( s ₀ ; Δ) определены равенствами

Анатолий Карацуба доказал, в частности, что если значения H и Δ превосходят некоторые достаточно малые константы, то оценки

Аргумент дзета-функции Римана

содержит как минимум

точки, в которых функция S ( t ) меняет знак. Ранее аналогичные результаты были получены Атле Сельбергом для случая

Представления

Серия Дирихле

Расширение области сходимости можно получить, переставив исходный ряд. Сериал

Интегралы типа Меллина

Преобразование Меллина функции f ( x ) определяется как

в области определения интеграла. Существуют различные выражения для дзета-функции в виде интегралов, подобных преобразованию Меллина. Если действительная часть s больше единицы, мы имеем

для всех s (где H обозначает контур Ганкеля ).

Тета-функции

Дзета-функция Римана может быть задана преобразованием Меллина

Однако этот интеграл сходится только в том случае, если действительная часть s больше 1, но его можно регуляризовать. Это дает следующее выражение для дзета-функции, которое хорошо определено для всех s, кроме 0 и 1:

Серия Laurent

Константы γ _n здесь называются константами Стилтьеса и могут быть определены пределом

интеграл

верно, что может быть использовано для численной оценки дзета-функции.

Растущий факториал

Это можно использовать рекурсивно, чтобы расширить определение ряда Дирихле на все комплексные числа.

Произведение Адамара

Глобально сходящийся ряд

Серия появилась в приложении к статье Хассе и была опубликована во второй раз Джонатаном Сондоу в 1994 году.

Хассе также доказал глобально сходящийся ряд

в той же публикации. Исследование Ярослава Благушина показало, что аналогичная эквивалентная серия была опубликована Йозефом Сером в 1926 году.

Представление ряда в натуральных числах через примитив

Представление ряда неполными полибернулли-числами

Функция ζ может быть представлена ​​при Re ( s )> 1 бесконечным рядом

Преобразование Меллина карты Энгеля

Представление ряда в виде суммы геометрического ряда

По аналогии с произведением Эйлера, которое может быть доказано с помощью геометрических рядов, дзета-функция для Re ( s )> 1 может быть представлена ​​в виде суммы геометрических рядов:

Численные алгоритмы

Классический алгоритм, использовавшийся примерно до 1930 г., основан на применении формулы Эйлера-Маклорена для получения для n и m положительных целых чисел

и ошибка удовлетворяет

Приложения

Бесконечная серия

Дзета-функция, вычисленная на эквидистантных положительных целых числах, появляется в бесконечных последовательностях представлений ряда констант.

Фактически, четный и нечетный члены дают две суммы

Параметризованные версии приведенных выше сумм даются формулами

где Im обозначает мнимую часть комплексного числа.

Еще больше формул можно найти в статье Число гармоник.

Обобщения

Существует ряд связанных дзета-функций, которые можно рассматривать как обобщения дзета-функции Римана. К ним относятся дзета-функция Гурвица

что совпадает с дзета-функцией Римана при z = 1 и q = 1 (нижний предел суммирования в трансценденте Лерха равен 0, а не 1).

Эти функции можно аналитически продолжить на n- мерное комплексное пространство. Специальные значения, принимаемые этими функциями при положительных целочисленных аргументах, теоретиками чисел называются множественными дзета-значениями и связаны со многими различными разделами математики и физики.

Источник