Что такое двухполюсник приведите пример
Пассивный и активный двухполюсники
Пассивный и активный двухполюсники. Теорема об активном двухполюснике
Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов). Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным.

Пассивный двухполюсник является потребителем энергии и может быть заменен
эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 1.15).
Активный двухполюсник ведет себя как генератор. Находящиеся внутри него нескомпенсированные источники отдают энергию во внешнюю цепь (рис. 1.16, а). Можно попытаться подобрать источник энергии с ЭДС ЕЭ и внутренним сопротивлением RЭ, который будет эквивалентен двухполюснику, то есть будет создавать во внешней цепи тот же самый ток (рис. 1.16, б).
Полученный генератор должен быть эквивалентен двухполюснику в любом режиме, в том числе и в режимах холостого хода и короткого замыкания. Источники энергии, входящие в состав активного двухполюсника, в режиме холостого хода создают на его зажимах напряжение UХ (рис. 1.17, а), а при коротком замыкании вызывают ток IK (рис. 1.17, б).
Из схем, приведенных на рис. 1.17, следует:
То есть, любой активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого ЕЭ равна напряжению холостого хода двухполюсника, а внутреннее сопротивление RЭ напряжению холостого хода, деленному на ток короткого замыкания.
Это утверждение и есть теорема об активном двухполюснике (эквивалентном генераторе).
Пример 1.4. Заменить активный двухполюсник, выделенный пунктиром на рис. 1.18, а, эквивалентным генератором (рис. 1.18, б). Численные значения параметров цепи составляют: Е1 = 200 В, Е2 = 100 В, R1 = 50 Ом, R2 = 20 Ом, R3 = 20 Ом.
Рис. 1.18. Замена активного двухполюсника (а) эквивалентным генератором (б).
Решение. Напряжение холостого хода, определяющее величину ЭДС эквивалентного генератора, можно найти по схеме на рис. 1.19, а любым известным способом.
Рис. 1.19. Режимы холостого хода (а) и короткого замыкания (б)
Воспользуемся, например, методом контурных токов. Принимая в качестве контурных токи I1Х для левого контура и I3Х для правого, записываем контурные уравнения, из которых определяем контурные токи:
Напряжение холостого хода – это напряжение между точками m и n. Оно равно падению напряжения на сопротивлении R3:
Таким образом, ЭДС эквивалентного генератора ЕЭ = 75 В.
Применим теперь метод узловых потенциалов.
Принимая потенциал узла n равным нулю (j n = 0), для узла m запишем узловое уравнение:

Из уравнения (1.12) имеем:
Получили тот же самый результат.
Приступаем к расчету режима короткого замыкания. Ток IK в схеме на рис. 1.19, б найдем методом наложения. При действии только первой ЭДС ее ток проходит по первой ветви и, минуя вторую и третью ветви, замыкается по проводнику, закорачивающему зажимы двухполюсника:
Аналогично находим ток, вызываемый второй ЭДС:
Ток в третьей ветви равен нулю, так как она закорочена.
В соответствии с теоремой об эквивалентном генераторе
№8 Пассивный и активный двухполюсники. Теорема об активном двухполюснике.
Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов).
Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным. Если в схеме двухполюсника имеются нескомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 8.1). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.
Пассивный двухполюсник является потребителем энергии и может быть заменен эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 8.2).
Активный двухполюсник ведет себя как генератор. Находящиеся внутри него нескомпенсированные источники отдают энергию во внешнюю цепь (рис. 8.3, а). Можно попытаться подобрать источник энергии с ЭДС ЕЭ и внутренним сопротивлением RЭ, который будет эквивалентен двухполюснику, то есть будет создавать во внешней цепи тот же самый ток (рис. 8.3, б).
Полученный генератор должен быть эквивалентен двухполюснику в любом режиме, в том числе и в режимах холостого хода и короткого замыкания. Источники энергии, входящие в состав активного двухполюсника, в режиме холостого хода создают на его зажимах напряжение UХ (рис. 8.4, а), а при коротком замыкании вызывают ток IK (рис. 8.4, б).
Из схем, приведенных на рис. 8.4, следует:

Итак, любой активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого ЕЭ равна напряжению холостого хода двухполюсника, а внутреннее сопротивление RЭ напряжению холостого хода, деленному на ток короткого замыкания.
Это утверждение и есть теорема об активном двухполюснике (эквивалентном генераторе).
Пример 1.4. Заменить активный двухполюсник, выделенный пунктиром на рис. 8.5, а, эквивалентным генератором (рис. 8.5, б). Численные значения параметров цепи составляют: Е1 = 200 В, Е2 = 100 В, R1 = 50 Ом, R2 = 20 Ом, R3 = 20 Ом.
Р е ш е н и е. Напряжение холостого хода, определяющее величину ЭДС эквивалентного генератора, можно найти по схеме на рис. 8.6, а любым известным способом.
Воспользуемся, например, методом контурных токов. Принимая в качестве контурных токи I1Х для левого контура и I3Х для правого, записываем контурные уравнения, из которых определяем контурные токи:
Напряжение холостого хода – это напряжение между точками m и n. Оно равно падению напряжения на сопротивлении R3:
Применим теперь метод узловых потенциалов.
Принимая потенциал узла n равным нулю (φn = 0), для узла m запишем узловое уравнение:
Из уравнения (1.12) имеем:
Получили тот же самый результат.
Приступаем к расчету режима короткого замыкания. Ток IK в схеме на рис. 8.6, б найдем методом наложения. При действии только первой ЭДС ее ток проходит по первой ветви и, минуя вторую и третью ветви, замыкается по проводнику, закорачивающему зажимы двухполюсника:
Аналогично находим ток, вызываем второй ЭДС:
Ток в третьей ветви равен нулю, так как она закорочена. Поэтому:
В соответствии с теоремой об эквивалентном генераторе
Двухполюсник
Смотреть что такое «Двухполюсник» в других словарях:
двухполюсник — Часть электрической цепи с двумя выделенными выводами. [ГОСТ Р 52002 2003] двухполюсник [Лугинский Я. Н. и др. Англо русский словарь по электротехнике и электроэнергетике. 2 е издание М.: РУССО, 1995 616 с.] Тематики электротехника, основные… … Справочник технического переводчика
ДВУХПОЛЮСНИК — многополюсник, имеющий только 2 точки подсоединения … Большой Энциклопедический словарь
двухполюсник — сущ., кол во синонимов: 1 • многополюсник (4) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
двухполюсник — (2 полюсник) … Орфографический словарь-справочник
Двухполюсник — Двухполюсник многополюсник, имеющий две точки подключения. Содержание 1 Описание двухполюсника 2 Простейшие двухполюсники … Википедия
двухполюсник — многополюсник, имеющий только 2 точки подсоединения. * * * ДВУХПОЛЮСНИК ДВУХПОЛЮСНИК, многополюсник (см. МНОГОПОЛЮСНИК), имеющий только 2 точки подсоединения … Энциклопедический словарь
двухполюсник — dvipolis statusas T sritis fizika atitikmenys: angl. port port network; two terminal network vok. Zweipol, m rus. двухполюсник, m pranc. bipôle, m; dipôle, m; réseau dipôle, m … Fizikos terminų žodynas
двухполюсник — 196 двухполюсник Часть электрической цепи с двумя выделенными выводами Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа … Словарь-справочник терминов нормативно-технической документации
двухполюсник — двухполюсник, двухполюсники, двухполюсника, двухполюсников, двухполюснику, двухполюсникам, двухполюсник, двухполюсники, двухполюсником, двухполюсниками, двухполюснике, двухполюсниках (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов
ДВУХПОЛЮСНИК — многополюсник, имеющий только две точки подсоединения. Различают Д. активные, содержащие источники электрич. энергии, и пассивные, не содержащие их (см. рис.). Осн. параметр пассивного Д. входное сопротивление z = U/I. Активный Д. эквивалентен… … Большой энциклопедический политехнический словарь
Тогда очевидно, что 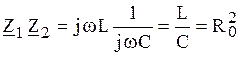
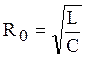
Условие дуальности реактивных двухполюсников можно записать в виде: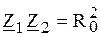
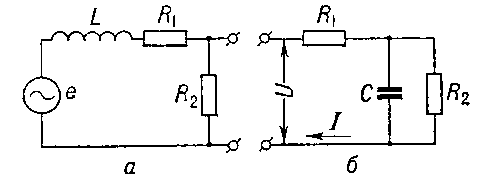
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, т.к. последовательно или параллельно соединённые однородные элементы могут быть заменены одним эквивалентным реактивным элементом того же характера. В результате получается так называемый приведенный двухполюсник.
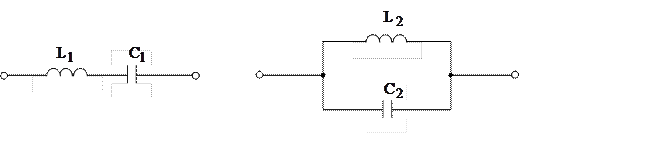
Определим комплексные сопротивления данных двухполюсников.


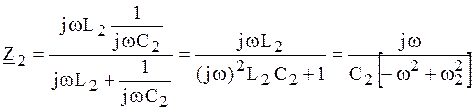
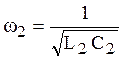
Определим соответствующие операторные сопротивления, осуществляя замену 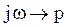
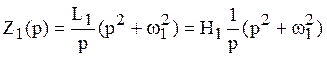
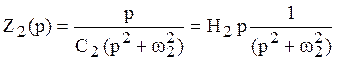
Приведённые реактивные двухполюсники представляют собой идеальные колебательные контура (последовательный и параллельный соответственно). Из курса ОТЦ Часть I известно, что в последовательном колебательном контуре наблюдается резонанс напряжений, а в параллельном колебательном контуре – резонанс токов. Следовательно:

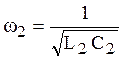
В дальнейшем частоты резонанса напряжений будем обозначать нечетными индексами: 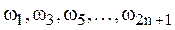


По первой частотной характеристике видно, что на частоте 
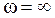

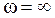

Так, например, идеальный последовательный контур имеет класс 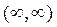
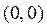


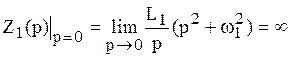
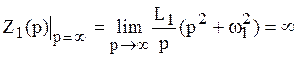
Можно определить класс реактивного двухполюсника непосредственно по схеме. Для этого составляют схемы замещения на частотах 
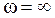

Многоэлементные реактивные двухполюсники

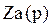

Преобразуем последнее выражение к так называемому каноническому виду:
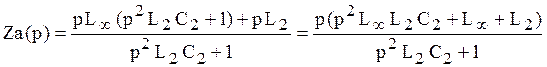
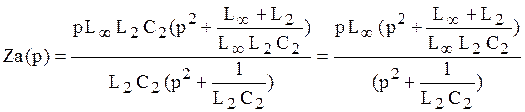
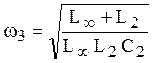
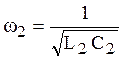
Тогда входное операторное сопротивление запишем как:
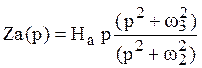
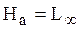
Построим частотную характеристику данного реактивного двухполюсника.
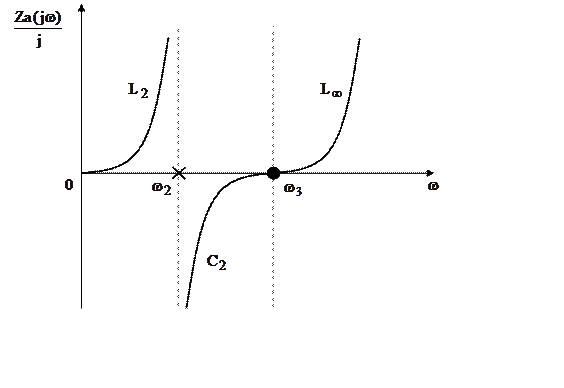 |
По данному рисунку можно сформулировать основные свойства входной функции РД.
1. Входная функция реактивных двухполюсников возрастает с ростом частоты;
2. Наблюдается чередование частот резонансов тока и напряжения, тем самым образуется так называемая диаграмма нулей и полюсов;
3. Число элементов двухполюсника превышает число резонансных частот на единицу;
4. Наибольшие и наименьшие степени полиномов числителя и знаменателя входной функции реактивного двухполюсника не могут отличаться более чем на единицу;
5. Наибольшая степень полинома числителя или знаменателя определяет количество элементов;
6. Если в выражении для входной функции множитель p располагается в числителе, то первым наступает резонанс тока, если множитель p располагается в знаменателе – резонанс напряжений.
Функция, обладающая такими свойствами, называется реактивной.
Построим эквивалентный реактивный двухполюсник, обладающий такой же частотной зависимостью, таким же классом 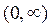
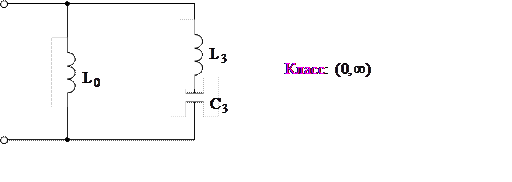 |
Определим операторное входное сопротивление эквивалентного реактивного двухполюсника.
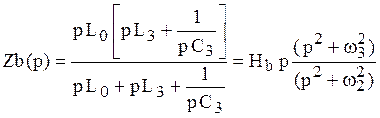
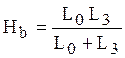
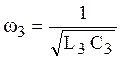
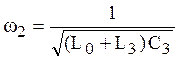
Соответствующую частотную характеристику можно представить в виде:
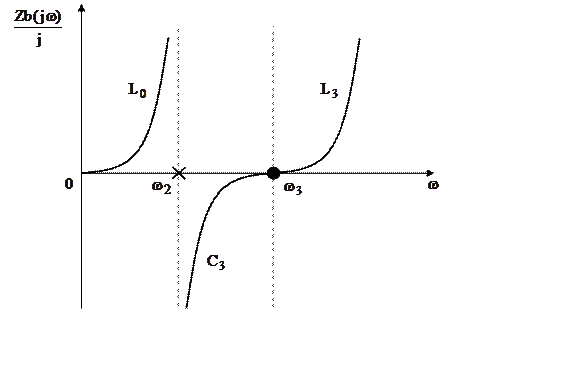 |
Необходимо установить связь между 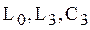
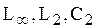

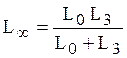
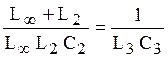
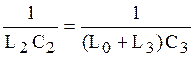
Задача для самостоятельного решения
Определить класс и построить эквивалентный реактивный двухполюсник. Из условия эквивалентности установить связь между параметрами двухполюсников. Привести график частотной зависимости входного сопротивления двухполюсников.
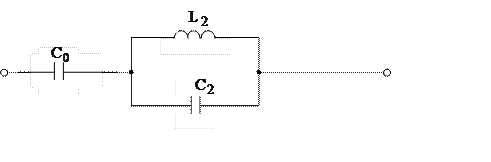 |
1. Что называется двухполюсником?
2. Как классифицируются двухполюсники?
3. Какие двухполюсники являются эквивалентными?
4. Какие двухполюсники являются реактивными?
5. Какова причина проявления частотных свойств двухполюсников?
6. Что собой представляет входная функция реактивных двухполюсников?
7. Что Вы понимаете под условием физической реализуемости?
8. Что такое положительная вещественная функция?
9. Какие основные свойства положительной вещественной функции Вы знаете?
10. Как определить вычет функции по полюсу первого порядка?
11. Какие реактивные двухполюсники являются дуальными?
12. Что собой представляет приведённый двухполюсник?
13. Как определить класс реактивного двухполюсника по схеме?
14. Как определить класс реактивного двухполюсника по виду операторного сопротивления?
15. Как определить класс реактивного двухполюсника по частотной характеристике реактивного сопротивления?
16. Какие основные свойства входной функции реактивных двухполюсников Вы знаете?
17. Какая входная функция называется реактивной?