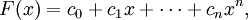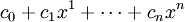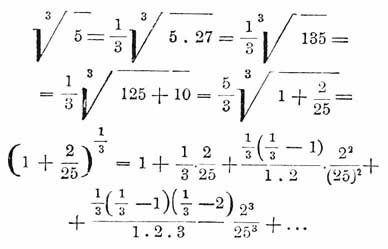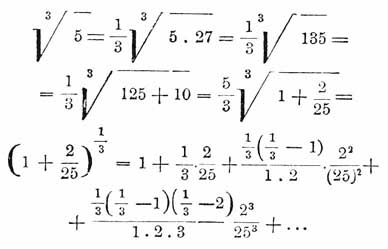Что такое двучлен в алгебре

Двучлен

где c_i фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.

Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.

Содержание

Определение

Многочлен (или полином) от n переменных — есть конечная формальная сумма вида

,

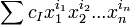
где I = (i₁,i₂. i_n) есть набор из целых неотрицательных чисел (называется мультииндекс), c_I — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.

В частности, многочлен от одной переменной есть конечная формальная сумма вида

Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается

Связанные определения

Делимость

Например, многочлен x 4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.

Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).

Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.

Полиномиальные функции

.

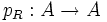
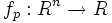
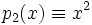
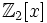
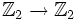
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены и из определяют тождественно равные функции .

Источник

Двучлен

(мат.) — В добавление сказанного в ст. Бином (см.) заметим по поводу бинома Ньютона. Уже Вьетту было известно, что от возвышения Д. а + b в какую угодно целую положительную степень n получается формула вида

где в правой части многочлен, состоящий из n+1 членов. В каждом из них сумма показателей над а и над b равна n. Кэффициенты же Р₁, Р₂. Р_n — суть некоторые целые числа. Ньютон первый показал закон составления этих коэффициентов. Коэфф. Р_k оказывается равным числу сочетаний из n предметов по k (см. Сочетания), или, выражая это формулой

Уже Ньютон, а за ним и все остальные математики, между прочим Эйлер, рассматривали формулу, приведенную выше, также и для n дробных и отрицательных. В этих случаях (а + b) n представляется уже не в виде многочлена с n+1 членами, а в виде бесконечного ряда, начинающегося с членов

а n + Р₁a n-1 b + Р₂а n-2 b 2 +.

причем Р_k вычисляется по формуле (2) и может не быть целым числом. Бесконечные ряды употребляются лишь в том случае, когда эти ряды суть так назыв. сходящиеся (см. Ряд). Полагая b/a = х, мы приходим к рассмотрению выражения (1+x) m или, другими словами, к нахождению суммы ряда

для всех значений х и n действительных или мнимых, для которых ряд сходящийся. Полное решение послднего вопроса представляет знаменитая работа норвежского математика Абеля: «Recherches sur la série 1 + (m/1)х +. (см. журнал Crell’я, т. I, 1826). Ограничиваясь вещественными значениями х и m, замечаем, что формула

1) при n целом и положительном справедлива, каково бы ни было значение х;

4) при х = — 1 имеет место, когда m > 0.

Бином Ньютона дает возможность вычислять корни по приближению. Например:

Вычисляя только написанные четыре члена, мы получим для 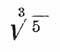число 1,70997858, в котором верны пять знаков после запятой.

Источник

Двучлен

Полезное

Смотреть что такое «Двучлен» в других словарях:

двучлен — двучлен … Орфографический словарь-справочник

двучлен — бином Словарь русских синонимов. двучлен сущ. • бином Словарь русских синонимов. Контекст 5.0 Информатик. 2012. двучлен … Словарь синонимов

ДВУЧЛЕН — (бином) алгебраическая сумма 2 одночленов … Большой Энциклопедический словарь

ДВУЧЛЕН — ДВУЧЛЕН, двучлена, муж. (мат.). Алгебраическое выражение, представляющее сумму или разность двух одночленов; то же, что бином. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ДВУЧЛЕН — ДВУЧЛЕН, а, муж. (спец.). Алгебраическое выражение многочлен, состоящий из двух одночленов. | прил. двучленный, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

двучлен — бином двучленный биномиальный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы биномдвучленныйбиномиальный EN binomial … Справочник технического переводчика

двучлен — а; м. Матем. Алгебраическое выражение, представляющее сумму или разность двух одночленов; бином. ◁ Двучленный, ая, ое. Д ое уравнение. * * * двучлен (бином), алгебраическая сумма 2 одночленов. * * * ДВУЧЛЕН ДВУЧЛЕН (бином), алгебраическая сумма 2 … Энциклопедический словарь

Двучлен — (в элементарной алгебре) алгебраическая сумма двух Одночленов. Д. часто называют также Биномом … Большая советская энциклопедия

Двучлен — м. Алгебраическое выражение, представляющее собою сумму или разность двух одночленов; бином (в математике). Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

двучлен — двучлен, двучлены, двучлена, двучленов, двучлену, двучленам, двучлен, двучлены, двучленом, двучленами, двучлене, двучленах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

Источник

Многочлен стандартного вида

Определение многочлена

Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».

Одночлен — это произведение, состоящее из числового множителя и одной или нескольких переменных, каждая из которых взята в неотрицательной степени.

Рассмотрим примеры многочленов:

Если многочлен состоит из двух одночленов, его называют двучленом:

Этот же многочлен можно записать вот так:

Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.

Многочлен вида 10x − 3x 2 + 7 называется трехчленом.

Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.

Если разделить многочлен с переменной x на линейный двучлен x − b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.

Если многочлен содержит обычное число — это число является свободным членом многочлена.

Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:

Такие выражения состоят из свободных членов.

Коэффициенты многочлена

Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.

Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.

Например:

Дан многочлен 2x + 5x − 18y

Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.

Многочлен стандартного вида

Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.

Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.

Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.

К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.

Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.

Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.

Дан красавец многочлен: 3x + 5xy 2 + x − xy 2

Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

Рассмотрим на примере:

Дан многочлен 6x + 4xy 2 + x + xy 2

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

Отсюда делаем вывод, что многочлен 7x + 5xy 2 — многочлен третьей степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy 2 + x + xy 2 — многочлен третьей степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Дан многочлен 6xx 2 + 5xx 2 − 3xx 3 − 3x 2 x

Приведем его к стандартному виду: 6xx 3 + 5xx 2 − 3xx 3 − 3x 2 x = 6x 4 + 5x 3 − 3x 4 − 3x 3

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

Практика

Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Многочлен приведен к стандартному виду.

Ответ: x 4 + x 2 y 3

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.

Источник

Алгебра. 7 класс

Конспект урока

Многочлены стандартного вида

Перечень рассматриваемых вопросов:

Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.

Многочлен, состоящий из двух членов, называется двучленом.

Многочлен, состоящий из трёх членов, называется трёхчленом.

Степенью многочлена стандартного вида называют наибольшую из степеней одночленов, входящих в этот многочлен.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

«Единственный путь, ведущий к знанию, – это деятельность», – сказал однажды ирландский драматург Джордж Бернард Шоу.

Сегодня наша деятельность будет заключаться в том, чтобы привести многочлен к стандартному виду.

Начнём с того, что вспомним, что такое многочлен.

Многочлен – это сумма одночленов.

Многочлен стандартного вида – это многочлен, каждый член которого является одночленом стандартного вида и который не содержит подобных членов.

Например, так могут выглядеть многочлены, приведённые к стандартному виду:

12a 2 bc 3 + ху 4 + 1,2ср 8 (трёхчлен)

2,5ас – 3к 2 х 5 (двучлен)

В них каждый член многочлена записан в стандартном виде, и ему нет подобных.

Стоит отметить, что многочлены могут иметь свои названия.

Например, многочлен, состоящий из двух членов, называется двучленом, из трёх членов – трёхчленом и т.д.

А так могут выглядеть многочлены нестандартного вида:

2abаc 3 + хху 4 + 1,2ср 8

2,5аса – 3к 2 х 5 к + 16

В этом случае некоторые члены многочленов находятся не в стандартном виде.

Рассмотрим правило приведения многочлена к стандартному виду:

1)каждый член многочлена нужно привести к стандартному виду;

2)привести подобные члены.

Пример:

Приведите к стандартному виду многочлен:

Следуя 1 пункту правила, приведём все члены многочлена к стандартному виду, но в данном задании все члены уже записаны в стандартном виде, т.е. вначале стоит число, а затем буквы в алфавитном порядке.

Следуя 2 пункту правила, приведём подобные члены. В данном многочлене они есть, выделим их.

В результате преобразования получается многочлен, записанный в стандартном виде.

Следуя данному правилу, любой многочлен можно привести к стандартному виду.

Рассмотрим ещё одно подобное задание.

Приведём к стандартному виду многочлен:

Решение: 3ab + 7c 2 –3ab – 7сс = 3ab + 7c 2 – 3ab – 7с 2 = 0

Следуя 1 пункту правила, приведём все члены многочлена к стандартному виду, в задании один член записан не в стандартном виде.

Следуя 2 пункту правила, приведём подобные члены. В многочлене они есть, выделим их.

В результате преобразования получается многочлен, записанный в стандартном виде, равный нулю. Такие многочлены называются нулевыми.

Введём ещё одно понятие, связанное с многочленами в стандартном виде – это степень многочлена.

Степенью многочлена стандартного вида называют наибольшую из степеней одночленов, входящих в этот многочлен.

12a 2 bc 3 + 7кх – многочлен 6 степени,

у данных многочленов степень соответственно шесть и семь. Т. к. у первого многочлена степени одночленов 6 и 2. А у второго многочлена степени одночленов 7, 1, 0. Выбираем большую степень и получаем степень многочлена.

Про первый многочлен говорят, что это многочлен шестой степени.

А про второй многочлен можно сказать – многочлен седьмой степени.

Если при выполнении заданий встретится многочлен с одинаковыми степенями слагаемых, например:

а + с

говорят, «это многочлен первой степени относительно а и с».

Стоит отметить, что, если все члены многочлена стандартного вида содержат одну и ту же букву, их принято располагать в многочлене от большей степени к меньшей, при этом свободный член ставится на последнее место.

Например, так будет выглядеть запись многочлена в стандартном виде:

2а 3 + 3а 2 – 6а + 12.

Итак, сегодня мы получили представление о том, как приводить многочлен в стандартный вид.

Это интересно!

Мы уже знаем, что многочлен – это сумма одночленов, которые, в свою очередь, представляют собой произведение числовых и буквенных множителей.

Самое интересное заключается в том, что многочлены иногда имеют специфические названия. Например, многочлен, состоящий из одного одночлена, можно назвать моном. Мономом можно назвать такие многочлены: 7 или а.

Если многочлен состоит из двух слагаемых, т.е. двух одночленов, то мы знаем, что это двучлен, но его ещё можно назвать бином, например, 12а + 5 – есть бином.

Если многочлен состоит из трёх слагаемых, т.е. трёх одночленов, то мы знаем, что это трёхчлен, но его ещё можно назвать трином, например, 12а 2 + а + 5.

Если слагаемых в многочлене больше трёх, то говорят просто – многочлен.

Кстати, при записи многочлен обозначают буквой «Р», от греческого слова «poly» – «многий», «многочисленный», поэтому многочлены в математике называют также полиномами.

Разбор заданий тренировочного модуля.

1. Найдите степень многочлена 5ах + 2а

Решение: сначала нужно посмотреть степень каждого члена многочлена.

У одночлена 5ах степень 2

У одночлена 2а степень 1. Так как наибольшая степень 2, то она и будет являться степенью данного многочлена.

2) Выберите и подставьте вместо * такой одночлен, чтобы многочлен получился 5 степени

7x 4 + 12x 3 – 3x 2 + 1 + *

Для начала нужно определить исходные степени всех членов многочлена.

У одночлена 7x 4 степень 4.

У одночлена 12x 3 степень 3.

У одночлена – 3x 2 степень 2.

У одночлена 1 степень 0. Следовательно, в данном случае нет одночлена со степенью 5. Посмотрим варианты ответа и выберем ответ с нужной нам степенью 5.

У одночлена 5х степень 1

У одночлена 2асх степень 3

У одночлена а 2 ск 2 степень 5. Это и есть верный ответ.

Источник