Что такое двоичный счетчик
Двоичные счетчики
Делители частоты следования
Цифровые счетчики импульсов и
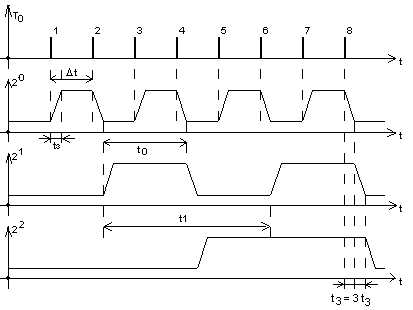
При рассмотрении диаграммы необходимо обратить внимание на то, что счетный вход каждого последующего триггера подключен к инвертирующему выходу предыдущего. Это означает, что положительный перепад на входе триггера, по которому он срабатывает, происходит при отрицательном перепаде по основному выходу предыдущего триггера. В диаграммах учтены задержки t3 (для простоты принятые одинаковыми), вызванные конечным временем переходного процесса триггера. По диаграммам легко убедиться, что значение двоичного кода на основных
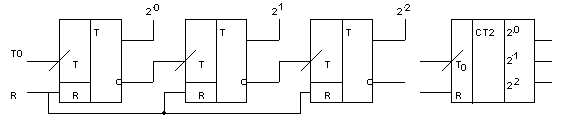
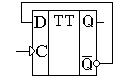
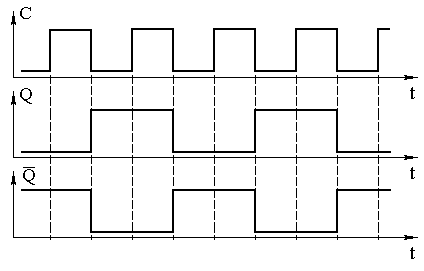
Рис. 5.15. Схема трехразрядного асинхронного суммирующего двоичного счетчика:
а, б – условное обозначение; в– временные диаграммы
выходах триггеров соответствует числу пришедших импульсов (см. на диаграммном состоянии после 5-го и 7-го импульсов). С приходом 7-го импульса информационная емкость счетчика исчерпывается и 8-й импульс приводит к последовательному сбросу в нулевое состояние всех триггеров, который заканчивается через время 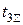
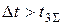
Такой счетчик называется асинхронным. С приходом каждого импульса число, отображаемое двоичным кодом, увеличивается на единицу, поэтому такой счетчик называется суммирующим.
Хорошо видно, что период следования импульсов с прямого выхода каждого последующего триггера в 2 раза больше, чем у предыдущего. Если снимать информацию, например, с выхода второго триггера, то частота следования импульса здесь будет в 4 раза ниже, чем у входных импульсов, т. е. счетчик может выполнять роль делителя частоты входных импульсов.
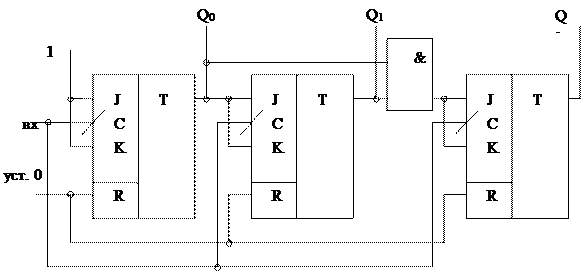
Ограничение скорости счета, вызванного у асинхронного счетчика последовательным переключением триггеров можно устранить, если осуществлять одновременное переключение триггеров, которое реализуется в счетчиках с параллельным переносом (рис. 5.16).
В это схеме входы J и K объединены и когда J=K=1 JK-триггер работает как Т-триггер, а когда J=K=0 – находится в режиме хранения. С помощью элемента И осуществляется перенос информации в старший разряд. Быстродействие повышается за счет того, чтос приходом входного импульса одновременно срабатывают все триггеры.
Рис. 5.16. Счетчик с параллельным переносом
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Счетчики
Счетчиком называется последовательное устройство, предназначенное для счета входных импульсов и фиксации их числа в двоичном коде.
Любые счетчики строятся на основе N однотипных связанных между собой разрядных схем, каждая из которых в общем случае состоит и TG и некоторой комбинационной схемы, предназначенной для формирования сигналов управления триггером.
Счетчик может выполнять следующие микрооперации над кодовым словом:
1.По значению модуля счета:
— двоичные, Мкот = целой степени числа 2 (М=2 n );
— двоично-кодированные, в которых М может принимать любое неравное целой степени числа 3, значение.
2.По направлению счета:
— суммирующие, выполняющие микрооперацию инкремента над хранящимся входным словом;
— вычитающие выполняющие микрооперацию декремента над хранящимся входным словом;
— реверсивные, выполняющие либо микрооперацию инкремента, либо декремента в зависимости от управляющего сигнала.
3.По способу организации межразрядных связей:
— счетчик с последовательным переносом, в котором переключение триггеров разрядных схем происходит последовательно один за другим;
— счетчик с параллельным переносом, в котором переключение всех триггеров разрядных схем происходит одновременно по сигналу синхронизации С;
— счетчик с комбинированным последовательно-параллельным переносом, когда используются различные комбинации способов переноса.
Как в схемах с параллельным, так и комбинированным переносом для подготовки счетчика к следующему переключению должно пройти время tкод=tзадержки логического элемента «И».
Схемы со сквозным переносом
Счётчики
Счётчики используются для построения схем таймеров или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах.
Вниманию любителей баннерорезок. Данная статья полностью искажается любыми антирекламными программами. Они очень не любят слово «счетчик», поэтому почти все рисунки вырезаются, насколько искажается текст не вчитывался 🙂
Двоичные асинхронные счётчики
Простейший вид счётчика — двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1.
Рисунок 1. Реализация счетного T-триггера на универсальном D-триггере
Так как схема T-триггера при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2.
Рисунок 2 Временные диаграммы сигналов на входе и выходах T-триггера
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Такой счетчик называется двоичным счетчиком, а тот факт, что состояние триггеров меняется на противоположное в различные моменты времени по мере распространения цифрового сигнала, отображается термином: асинхронный двоичный счетчик.
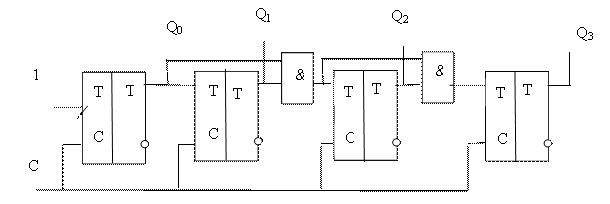
Рисунок 3. Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах
Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4.
Рисунок 4 Временная диаграмма четырёхразрядного счётчика
Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.
Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.
Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса.
Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
Таблица 1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
Условно-графическое обозначение суммирующего двоичного счетчика на принципиальных схемах приведено на рисунке 5. В двоичных счётчиках обычно предусматривают вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение. Это состояние иногда называют исходным состоянием счётчика.
Рисунок 5. Четырёхразрядный двоичный счётчик
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Подобные схемы существуют и внутри САПР программируемых логических интегральных схем.
Двоичные вычитающие асинхронные счётчики
Счётчики могут не только увеличивать своё значение на единицу при поступлении на счётный вход импульсов, но и уменьшать его. Такие счётчики получили название вычитающих счётчиков. Для реализации вычитающего счётчика достаточно чтобы T-триггер изменял своё состояние по переднему фронту входного сигнала.
Изменить рабочий фронт входного сигнала можно инвертированием этого сигнала. В схеме, приведенной на рисунке 6, для реализации вычитающего счётчика сигнал на входы последующих триггеров подаются с инверсных выходов предыдущих триггеров.
Рисунок 6 Схема четырёхразрядного двоичного вычитающего счётчика, построенного на универсальных D-триггерах
Временная диаграмма этого счётчика приведена на рисунке 7. По этой диаграмме видно, что при поступлении на вход счётчика первого же импульса на выходах появляется максимально возможное для четырёхразрядного счётчика число 1510. При поступлении следующих импульсов содержимое счётчика уменьшается на единицу.
Рисунок 7. Временная диаграмма четырёхразрядного вычитающего счётчика
Это вызвано тем, что при поступлении переднего фронта тактового импульса первый триггер переходит в единичное состояние. В результате на его выходе тоже формируется передний фронт. Он поступает на вход второго триггера, что приводит к записи единицы и в этот триггер. Точно такая же ситуация складывается со всеми триггерами счётчика, то есть все триггеры перейдут в единичное состояние. Для четырёхразрядного счётчика это и будет число 1510. Запишем новое состояние вычитающего счётчика в таблицу 2.
Следующий тактовый импульс приведёт к изменению состояния только первого триггера, так как при этом на его выходе сформируется задний фронт сигнала. Запишем и это состояние в таблицу 2. Обратите внимание, что при поступлении каждого последующего импульса содержимое счётчика, построенного по анализируемой схеме, уменьшается на единицу. Этот процесс продолжается до тех пор, пока состояние счётчика не станет вновь равно 0. При поступлении новых тактовых импульсов процесс повторяется снова.
Все возможные состояния логических сигналов на выходах вычитающего счётчика, при поступлении на счётный вход схемы тактовых импульсов приведены в таблице 2. Таблица 2 фактически повторяет временные диаграммы, приведённые на рисунке 7, однако она более наглядно представляет физику работы счётчика. Просто мы при работе с числами привыкли иметь дело с цифрами, а не с напряжениями, тем более в зависимости от времени.
Таблица 2. Изменение уровней на выходе вычитающего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 0 | 1 | 1 | 1 |
| 10 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 1 |
| 12 | 0 | 1 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 |
| 14 | 0 | 0 | 1 | 0 |
| 15 | 0 | 0 | 0 | 1 |
Для тех, кто привык работать с реально выпускаемыми микросхемами средней интеграции, следует обратить внимание, что для примера были использованы D-триггеры, работающие по заднему фронту. Микросхемы, выпускаемые промышленностью, например, 1533ТМ2 (два D-триггера в одном корпусе) или SN74LVC1G79 (микросхемы малой логики) срабатывают по переднему фронту, поэтому схемы для суммирующего и вычитающего счётчика поменяются местами.
Следует отметить, что при применении для реализации двоичных счетчиков современных схем большой интеграции, таких как программируемые пользователем вентильные матрицы FPGA, мы можем применять D-триггеры срабатывающие как по переднему (нарастающему), так и по заднему (спадающему фронту).
Понравился материал? Поделись с друзьями!
Вместе со статьей «Асинхронные счётчики» читают:
Электроника
учебно-справочное пособие
Счётчики
Счетчик импульсов — это последовательностное цифровое устройство, обеспечивающее хранение слова информации и выполнение над ним микрооперации счета, заключающейся в изменении значения числа в счетчике на 1. По существу счетчик представляет собой совокупность соединенных определенным образом триггеров. Основной параметр счетчика — модуль счета. Это максимальное число единичных сигналов, которое может быть сосчитано счетчиком.
Счетчики импульсов классифицируют
по направлению счета:
по способу формирования внутренних связей:
Двоичные асинхронные счётчики
В этой схеме, так как на вход триггера подается сигнал с инверсного выхода микросхемы, при поступлении тактовых импульсов сигнал на выходе будет меняться с 0 на 1 и наоборот. Временная диаграмма сигналов на входе и выходах триггера приведена на рисунке 2.
Таким образом у нас появился счётчик, считающий до двух. Обычно требуется посчитать количество импульсов, которое больше двух. В этом случае можно использовать выходной сигнал счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два.
Схема счётчика, позволяющего посчитать до 16 импульсов приведена на рисунке 3, а временная диаграмма сигналов на входе и выходах этого счётчика приведена на рисунке 4.
Как видно из временной диаграммы, на выходах этого двоичного счётчика последовательно появляются цифры от 0 до 15. Естественно эти цифры записаны в двоичном виде. Они приведены в таблице 1. То есть, при поступлении на счётный вход очередного импульса, содержимое счётчика увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
| Номер входного импульса | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Её изображение на принципиальных схемах приведено на рисунке 5. В этой микросхеме существует вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение.
Двоичные вычитающие асинхронные счётчики
Счётчики могут не только увеличивать своё значение на единицу при поступлении на вход импульсов но и уменьшать его. Такие счётчики получили название вычитающих счётчиков. Для реализации вычитающего счётчика достаточно чтобы T-триггер срабатывал по переднему фронту входного сигнала. Это можно осуществить инвертированием этого сигнала. В схеме, приведенной на рисунке 6, для реализации вычитающего счётчика сигнал на входы последующих триггеров подаются с инверсных выводов предыдущих триггеров.
Временная диаграмма этого счётчика приведена на рисунке 7. По этой диаграмме видно, что при поступлении на вход счётчика первого же импульса на выходах появляется максимально возможное для четырёхразрядного счётчика число 15. При поступлении следующих импульсов содержимое счётчика уменьшается на единицу. Этот процесс продолжается до тех пор, пока содержимое счётчика не станет вновь равно 0.
Все возможные состояния сигналов на выходах счётчика при поступлении импульсов на вход микросхемы приведены в таблице 2.
| Номер входного импульса | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 0 | 1 | 1 | 1 |
| 10 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 1 |
| 12 | 0 | 1 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 |
| 14 | 0 | 0 | 1 | 0 |
| 15 | 0 | 0 | 0 | 1 |
Для тех, кто привык работать с реально выпускаемыми микросхемами, следует обратить внимание, что для примера были использованы D-триггеры, работающие по заднему фронту. Микросхемы 1533ТМ2 (два D-триггера в одном корпусе) срабатывают по переднему фронту, поэтому схемы для суммирующего и вычитающего счётчика поменяются местами.
Недвоичные счётчики с обратной связью.
Если посмотреть на временную диаграмму сигналов на выходах двоичного счётчика, приведённого на рисунке 4, то можно увидеть, что частота сигналов на его выходах будет уменьшаться в два раза по отношению к предыдущему выходу. Это позволяет использовать счетчики в качестве делителей частоты входного сигнала. Эти делители частоты могут быть использованы в устройствах формирования высокостабильных генераторов частоты (синтезаторов частот). Частоты могут быть использованы либо для синхронизации цифровых устройств (в том числе и микропроцессоров) либо в качестве задающих генераторов радиоприёмных и радиопередающих устройств.
При использовании цифровых счётчиков в качестве устройств формирования опорных частот может потребоваться обеспечить коэффициент деления, отличающийся от степени числа 2. Ещё одна ситуация, когда необходимо применять недвоичные счётчики возникает при отображении информации, записанной в счётчике. Человек, который работает с электронной техникой, привык работать с десятичной системой счисления, поэтому возникает необходимость отображать хранящееся в счётчике число в непосредственно десятичном виде. Это намного проще сделать, если и счет вести сразу в двоично-десятичном коде. Иначе для индикации потребуется перекодировать информацию из двоичного в двоично-десятичный код.
Построить недвоичный счётчик можно из двоичного за счёт выбрасывания лишних комбинаций единиц и нулей. Это может быть осуществлено при помощи обратной связи. Для этого при помощи дешифратора определяется число, соответствующее коэффициенту счёта, и сигнал с выхода этого дешифратора обнуляет содержимое двоичного счётчика. В качестве примера на рисунке 8 приведена схема двоично-десятичного счётчика.
В этой схеме дешифратор построен на двухвходовой схеме «2И», входящей в состав микросхемы двоичного счётчика. Дешифратор декодирует число 10 (1010 в двоичной системе счисления). В соответствии с принципами построения схем по произвольной таблице истинности для построения дешифратора требуется ещё два инвертора, подключённых к выходам 1 и 4. Однако после сброса счётчика числа, большие 10 никогда не смогут появиться на выходах микросхемы. Поэтому схема дешифратора упрощается и вместо четырёхвходовой схемы «4И» можно обойтись двухвходовой схемой. Инверторы тоже оказываются лишними.
При использовании счётчиков в качестве делителей частоты тоже можно воспользоваться обратной связью. Приведём в качестве примера схему делителя частоты на 1000. При разработке делителя прежде всего определим сколько потребуется микросхем двоичных счётчиков. Для этого определим степень числа 2, при которой число M=2 n будет больше требуемого числа 1000. Это будет число 10. При возведении основания системы счисления 2 в 10 степень получится число 1024. То есть, при использовании для построения делителя частоты непосредственно триггеров, достаточно будет десяти триггеров. Однако обычно для построения делителей частоты используют готовые двоичные счётчики, поэтому определим необходимое количество микросхем двоичных счётчиков. При использовании четырёхразрядных двоичных счётчиков достаточно будет трёх микросхем, так как в трёх микросхемах будет 3*4=12 триггеров, что заведомо больше минимального числа триггеров.
Следующим этапом построения делителя частоты будет перевод коэффициента деления 1000 в двоичное представление. Десятичное число 1000 в двоичном виде будет выглядеть как 0011 1110 1000. В этом числе шесть единиц, поэтому для построения делителя будет достаточно шестивходовой схемы «И». Однако такие схемы не выпускаются, поэтому воспользуемся микросхемой «8И-НЕ». Неиспользуемые входы этой микросхемы подключим к питанию. Ненужную нам инверсию сигнала скомпенсируем дополнительным инвертором. Получившаяся схема делителя на 1000 приведена на рисунке 9.
При использовании счётчиков в составе синтезаторов частот может потребоваться формирование целого диапазона частот. В этом случае делитель должен обладать возможностью изменения коэффициента деления (ДПКД). При использовании обратной связи для этого потребуется полный дешифратор и переключатели его выходов на вход сброса счётчика. Схема при этом получается сложной, а управление неудобным. Пример двухразрядного делителя с переменным коэффициентом деления (ДПКД), построенного на десятичных счётчиках приведён на рисунке 4.
Источники
Электроника © ЦДЮТТ • Марсель Арасланов • 2019