Что такое двоичный поиск
Бинарный поиск в C++: подробное руководство
Сегодня мы и изучим его. Также попытаемся ответить на такие вопросы: как бинарный поиск работает в программе, плюсы и минусы его использования у себя в коде и в каких структурах данных можно его применять, а в каких нет. Поехали!
Что такое бинарный поиск
Линейный поиск по сравнению с бинарным — дешевая подделка. Бинарный поиск — очень быстрый алгоритм с не сложной реализацией, который находит элемент с определенным значением в уже отсортированном массиве.
Очень важно помнить! Алгоритм будет работать правильно, только с отсортированным массивом. А если по случайности вы забыли отсортировать массив перед его использованием, то в большинстве случаев тот ответ, который подсчитал алгоритм, будет неверным.
Принцип работы бинарного поиска
Самым легким и самым долгим по времени решением, будет поочередная проверка пассажиров в комнате с прибором (это линейный поиск). Но это слишком долго.
В задаче выше охранники использовали алгоритм двоичного поиска для нахождения диверсанта. В обычной программе принцип работы бинарного поиска такой же, как и в примере, выше.
Как создать бинарный поиск в C++
Давайте посмотрим как работает бинарный поиск на примере.В примере ниже в строке 9 мы создали массив arr на 10 элементов и в строке 12 предложили пользователю с клавиатуры заполнить его ячейки.
В строке 20 мы предлагаем пользователю ввести ключ (который нужно будет найти в массиве), а дальше мы с бинарным поиском проверим массив на наличие введенного ключа пользователем. Если мы найдем ключ в массиве, то выведем индекс ячейки, в которой находится ключ.
Национальная библиотека им. Н. Э. Баумана
Bauman National Library
Персональные инструменты
Двоичный поиск
Целочисленный двоичный поиск (бинарный поиск) (англ. binary search) — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.
Содержание
Алгоритм двоичного поиска
Алгоритм может быть определен в рекурсивной и нерекурсивной формах. Количество шагов поиска определится как log2n↑, где n-количество элементов, ↑ — округление в большую сторону до ближайшего целого числа. На каждом шаге осуществляется поиск середины отрезка по формуле mid = (left — right)/2 Если искомый элемент равен элементу с индексом mid, поиск завершается. В случае если искомый элемент меньше элемента с индексом mid, на место mid перемещается правая граница рассматриваемого отрезка, в противном случае — левая граница.
Подготовка Перед началом поиска устанавливаем левую и правую границы массива:
Шаг 1 Ищем индекс середины массива (округляем в меньшую сторону):
Шаг 2 Ищем индекс середины массива (округляем в меньшую сторону):
Шаг 3 Ищем индекс середины массива (округляем в меньшую сторону):
Шаг 4 Ищем индекс середины массива (округляем в меньшую сторону):
Шаг 5 Ищем индекс середины массива (округляем в меньшую сторону):
Чтобы уменьшить количество шагов поиска можно сразу смещать границы поиска на элемент, следующий за серединой отрезка:
left = mid + 1 right = mid — 1
Поиск элемента в отсортированном массиве
Приложения
Практические приложения метода двоичного поиска разнообразны:
Двоичный (бинарный) поиск.
Когда поиск некоторого элемента необходимо осуществить в упорядоченной по возрастанию или убыванию последовательности, тогда применѝм алгоритм двоичного (бинарного) поиска. Метод использует стратегию «разделяй и властвуй», а именно: заданная последовательность делится на две равные части и поиск осуществляется в одной из этих частей, которая потом также делится надвое, и так до тех пор, пока обнаружится наличие искомого элемента или его отсутствие.
Использовать эту операцию, уменьшая каждый раз зону поиска вдвое, позволительно лишь исходя из того факта, что элементы последовательности заранее упорядочены. Найдя средний элемент (сделать это, зная число элементов массива, не составит труда), и сравнив его значение с искомым, можно уверено сказать, где относительно среднего элемента находится искомый элемент.
Далее, будем полагать, что элементы массива располагаются в порядке возрастания, поскольку нет существенной разницы, как именно они упорядочены: по возрастанию или убыванию значение. Также обозначим границы зоны поиска через left и right – крайний левый и крайний правый элементы соответственно.
Ход работы алгоритма, разделенный на этапы, выглядит следующим образом:
В таблице ниже представлен конкретный целочисленный массив, и пошаговое выполнение алгоритма бинарного поиска применительно к его элементам. Для экономии места в таблице left, right и mid заменены на a, b и c.
Имеется последовательность целых чисел, расположенных в порядке возрастания, а также ключ – число 16. Изначально граничными элементами являются элементы с номерами 1 и 9, и значениями 1 и 81. Вычисляется номер среднего элемента, для чего, как правило, используется формула (right+left)/2, либо left+(right-left)/2 (далее, в программах будет использована вторая формула, как наиболее устойчивая к переполнениям). После сравнения оказывается, что искомый элемент меньше среднего, и поэтому последующий поиск осуществляется в левой части последовательности. Алгоритм продолжает выполняться подобным образом, до нахождения на 4 шаге искомого элемента.
Стоит отметить, что здесь потребуется гораздо меньше времени, чем, если бы мы воспользовались линейным поиском, но в отличие от линейного поиска двоичный работает только с массивами, элементы которых упорядочены, что, несомненно, придает ему отрицательной специфичности.
Двоичный поиск
Основные авторы описания: А. В. Чупин.
Синонимы названия метода: двоичный поиск, бинарный поиск, метод деления пополам, метод половинного деления, дихотомия.
Содержание
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод двоичного поиска используется в качестве быстрого варианта поиска в заранее отсортированном массиве. Получил распространение благодаря как наименьшей из возможных высоте алгоритма, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи.
Основная идея заключается в дроблении массива на половины и дальнейшем рекурсивном поиске в одной из них.
Альтернативой служит метод линейного поиска (то есть полного перебора), имеющий, соответственно, линейную вычислительную сложность ( [math]O(n)[/math] ), однако работающий на произвольно упорядоченных массивах. Если сравнивать возможности применения обоих методов, то линейный поиск выгоднее применять 1) для поиска в коротких массивах; 2) когда требуется провести поиск небольшое число раз; 3) в потоковом случае. В отличие от него, бинарный поиск требует предобработку (сортировку, сложность которой не менее [math]O(n \log_2 n)[/math] ) и особенно полезен, если массив большой и поиск проводится неоднократное (точнее, более, чем порядка [math]O(\log_2 n)[/math] ) число раз.
Метод позволяет различные обобщения и видоизменения:
Вариации также могут касаться формата и сути вывода результата в отдельных случаях (см. варианты возврата при ненахождении).
Очень близко к метод бинарного поиска по массиву стоит непрерывный аналог — метод бисекции (метод деления пополам) нахождения корня непрерывной функции на заданном отрезке. Самое большое отличие заключается в вычислении значения функции вместо нахождения элемента массива по его индексу, а также использование действительных чисел в качестве аргумента в отличие от целых чисел для индексации элементов массива.
По своему определению, алгоритм может быть записан в одной из двух основных форм — рекурсивной и итеративной. Поскольку вычислительное ядро в них одинаковое, но в рекурсивном есть дополнительная нагрузка по вызову функций и хранению их стека, в данной статье рассматривается только итеративная версия.
1.2 Математическое описание алгоритма
Вычисляемые данные: индекс (номер позиции) элемента, равного искомому (или ответ, что такого элемента нет).
1.3 Вычислительное ядро алгоритма
1.4 Макроструктура алгоритма
По определению алгоритм состоит из рекурсивных вызовов самого себя для меньших массивов. Стандартные макрооперации не используются.
1.5 Схема реализации последовательного алгоритма
В рекурсивном варианте определяется функция, принимающая в числе прочих параметров индексы концов отрезка массива, на котором идёт текущий поиск, а операция «идём к шагу 2» означает вызов той же функции поиска с другими индексами концов отрезка.
В итеративном варианте пп. 2-5 обёрнуты в бесконечный цикл, выход из которого возможен либо в п. 2 (как неуспешный), либо в п. 5, когда значение найдено.
1.6 Последовательная сложность алгоритма
Таким образом, алгоритм обладает логарифмической временной сложностью по данным и даже последовательная реализация достаточно быстра и, в принципе, не нуждается в распараллеливании.
1.7 Информационный граф
Граф алгоритма является параметризованным (зависит от размера массива) и недетерминированным (в смысле, что порядок вычислений зависит от начальных данных).
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
Дополнительные ограничения: массив упорядочен.
Выходные данные: индекс элемента [math]A[/math] в массиве, если он есть.
Объём выходных данных: один скаляр.
1.10 Свойства алгоритма
Алгоритм абсолютно устойчив, так как действия производятся только над целыми числами, и поэтому погрешность всегда равна 0.
2 Программная реализация алгоритма
Возможная простейшая реализация алгоритма на языке C:
Здесь ряд индексов [math]l_k, m_k, r_k[/math] из математической схемы алгоритма превращён в одну переменную, поскольку требуются только последние значения этих рядов.
2.1 Особенности реализации последовательного алгоритма
Обычно в качестве ответа выводят −1, если число не найдено.
Другие возможные варианты в данной ситуации (выбор зависит от того, как и где будет использоваться метод поиска как базовая единица) [8] :
2.1.1 Частые ошибки при реализации
Несмотря на то, что код достаточно прост, в нём есть несколько ловушек, на которые нужно обратить внимание [9] :
2.2 Локальность данных и вычислений
Пространственная локальность достаточно плохая — начальные обращения в память гарантированно далеки друг от друга. Однако расстояние с номером итерации экспоненциально уменьшается и в конце есть надежда на использование преимуществ локальности обращений.
Временная локальность ещё хуже — один и тот же элемент массива никогда не требуется дважды.
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
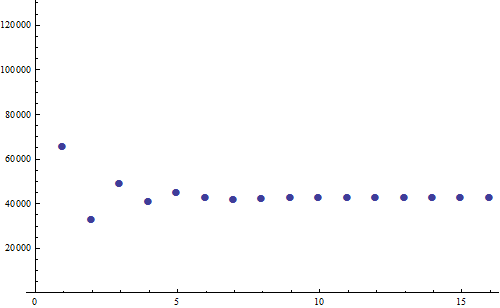
На рис. 3 представлен профиль обращений в память для реализации последовательного алгоритма двоичного поиска. В программе задействован массив и три переменные, на рисунке показаны обращения только к элементам этого массива. Каждая точка соответствует одной итерации алгоритма.
Видно, что на каждой итерации используется одна ячейка памяти, при этом адреса располагаются достаточно хаотично. Пространственная локальность от очень плохой постепенно улучшается до идеальной, когда идут обращения только в близкие ячейки памяти. Данные из массива никогда не используются повторно, поэтому временная локальность плохая.
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
Однако при этом потребуется предусмотреть обмен результатами сравнения своей точки деления на каждом процессоре для определения искомого интервала для следующей итерации. Это потребует минимум одной коллективной операции обмена, что ставит под сомнение эффективность распараллеливания.
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
Использовать алгоритм в любой реализации для архитектур с разделённой памятью смысла не имеет — из-за нелокального доступа к исходным данным и малого количества вычислительных операций даже в параллельной модификации выигрыш будет съедаться коммуникациями.
Применение систем с общей памятью с помощью OpenMP теоретически имеет смысл, однако для получения хоть какого-то ускорения требуется выполнение нескольких условий:
30 поискам в массиве из миллиарда элементов).
Бинарный поиск
Линейный поиск
Мы считаем, что вы уже знаете линейный поиск, а именно умеете решать задачи такого типа:
Задание
Убедитесь, что вы умеете решать эти задачи. Докажите, что быстрее, чем O(n) их решить в худшем случае нельзя.
Бинарный поиск
Однако иногда найти число X в массиве можно и быстрее! Для этого надо добавить условие на то, что массив отсортирован. Но давайте начнем не с этого.
Задание
Я загадал число X от 1 до 100. Вы можете спрашивать, больше ли мое число чем число T, я отвечаю “да” или “нет”. За сколько вопросов в худшем случае вы сможете найти число X? Как нужно действовать?
Почему нужно делить обязательно пополам? Почему бы не спросить “число X больше, чем 80?” первым же вопросом? Но если вдруг ответ “нет”, то мы останемся с 80 вариантами вместо 100. То есть деление отрезка ровно пополам гарантирует, что в худшем случае мы останемся не более чем с половиной вариантов.
Теперь вернёмся к нашей задаче. Можно понять, что такой алгоритм работает как раз за \(O(\log n)\) вопросов (если число 100 на заменить абстрактную переменную \(n\) ). Несложно убедиться, что именно логарифм раз нужно поделить число на два, чтобы получилось 1.
Общий принцип
А теперь представьте такую задачу: у вас есть массив, состоящий из некоторого количества подряд идущих нулей, за которыми следует какое-то количество подряд идущих единиц.
Вам дан массив, и вам нужно найти позицию первой единицы, то есть найти такое место, где заканчиваются нули, и начинаются единицы. Это можно сделать с помощью линейного поиска за один проход по массиву, но хочется сделать это быстрее.
Есть много способов писать бинарный поиск, и в его написании люди очень часто путаются. Очень удобно в данном случае воспользоваться инвариантом (это слово значит “постоянное свойство”):
Пусть переменная left всегда указывает на \(0\) в массиве, а переменная right всегда указывает на \(1\) в массиве.
Дальше мы будем переменные left и right постепенно сдвигать друг к другу, и в какой-то момент они станут соседними числами. Это и будет означать, что мы нашли место, где заканчиваются нули и начинаются единицы.
Осталось нам написать цикл while :
Мы решили задачу для ноликов и единичек, но это легко обобщается на абсолютно любую задачу, где есть какое-то свойство, которое в начале массива не выполняется, а потом выполняется.
Задание
Поэтому зачастую такие задачи сформулированы таким образом:
Задание
Найдите время работы, за которое решается эта задача?